Ромб - это геометрическая фигура, которая имеет особые свойства и характеристики. Одна из ключевых характеристик ромба - это его диагональ. Диагональ ромба - это отрезок, соединяющий две противоположные вершины. Нахождение длины диагонали ромба позволяет решать множество задач и применять ромбы в различных областях.
Существует несколько способов расчета диагонали ромба, в зависимости от известных данных. Один из способов - использование формулы, которая позволяет найти длину диагонали, если известны длина стороны ромба и углы между диагоналями и сторонами. Формула для расчета длины диагонали ромба выглядит следующим образом:
d = sqrt(a^2 + b^2), где d - диагональ ромба, a - длина одной стороны ромба, b - длина другой стороны ромба.
Если известна площадь ромба, то можно воспользоваться другой формулой для нахождения длины диагонали:
d = sqrt(4 * S / h), где d - диагональ ромба, S - площадь ромба, h - высота ромба.
Также существуют геометрические способы нахождения диагонали ромба, основанные на свойствах фигуры. Один из таких способов - провести два перпендикулярных отрезка, соединяющих вершины ромба. Эти отрезки будут прямыми проекциями диагоналей ромба на его стороны. Зная длины этих отрезков и рассчитав углы, можно использовать тригонометрические соотношения для нахождения диагонали.
Определение диагонали ромба является важным шагом при решении задач и применении ромбов в различных сферах, таких как архитектура, геодезия, графика и дизайн. Правильное использование формул и методов позволяет точно и эффективно рассчитывать диагональ ромба и получать достоверные результаты.
Ромб - определение и свойства
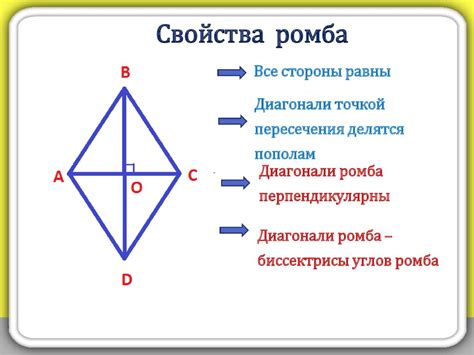
Первое свойство ромба заключается в его симметрии. Ромб является фигурой, у которой существуют несколько осей симметрии. Линии симметрии ромба проходят через середины его сторон, а также через его углы. Благодаря этим осям, все отрезки, соединяющие противоположные углы ромба, делят его на две равные части.
Второе свойство ромба связано с его диагоналями. Диагонали ромба являются перпендикулярными и делят его на 4 равных треугольника. Если обозначить сторону ромба как "a", то его диагонали можно выразить через "a" с помощью формулы:
Диагональ 1 = a * √2
Диагональ 2 = a * √2
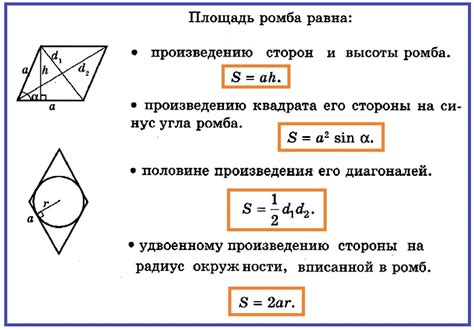
Третье свойство ромба связано с его площадью и периметром. Площадь ромба можно вычислить по формуле:
Площадь = (длина диагонали 1 * длина диагонали 2) / 2
Периметр ромба можно вычислить по формуле:
Периметр = 4 * сторона
Ромб имеет множество применений в различных областях, таких как геометрия, архитектура, дизайн и др. Его симметрия и уникальные свойства делают его одной из наиболее интересных и полезных фигур в математике.
Как найти диагональ ромба по стороне
Формула для нахождения диагонали ромба по стороне выглядит следующим образом:
Диагональ = Сторона * √2
Для расчета диагонали ромба нужно знать длину одной из его сторон. Воспользовавшись данной формулой, можно легко и быстро определить длину диагонали.
Кроме использования формулы, существует еще один способ нахождения диагонали ромба по стороне. Для этого нужно провести прямую линию, соединяющую противоположные вершины ромба. Получившаяся линия будет являться диагональю ромба. Затем можно измерить длину полученной линии с помощью линейки или другого измерительного инструмента.
Теперь вы знаете, как найти диагональ ромба по стороне с помощью формулы и проведения линии. Эти методы позволяют быстро и точно определить длину диагонали ромба, что может быть полезно при решении различных геометрических задач.
Как найти диагональ ромба по углу
Шаг 1: Узнайте значение угла ромба в градусах.
Шаг 2: Возьмите тангенс угла ромба и разделите его на 2. Полученный результат помножьте на длину одной стороны ромба.
Формула выглядит следующим образом:
Диагональ = 2 * (тангенс угла) * (длина стороны)
Таким образом, имея значение угла и длину стороны ромба, вы можете легко вычислить длину диагонали. Это пригодится вам, когда вам потребуется решать задачи, связанные с конструкцией ромбов или нахождением их параметров.
Примеры расчета диагонали ромба
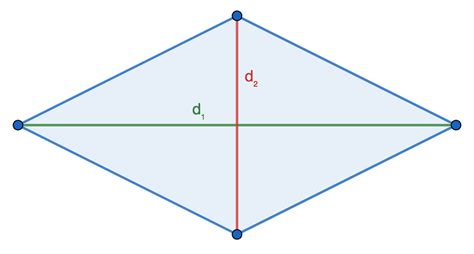
Пример 1: Допустим, у нас есть ромб со стороной длиной 6 см. Для нахождения диагонали ромба, мы можем использовать теорему Пифагора. Согласно этой теореме, квадрат длины диагонали ромба равен сумме квадратов половины длины ромба:
Длина диагонали12 = половина длины стороны2 + половина длины стороны2
Длина диагонали12 = 6 см/22 + 6 см/22
Длина диагонали12 = 3 см2 + 3 см2
Длина диагонали12 = 9 см2
Длина диагонали1 = √9 см
Длина диагонали1 = 3 см
Таким образом, длина диагонали ромба в данном примере равна 3 см.
Пример 2: Предположим, у нас есть ромб со стороной длиной 8 см. Используем ту же формулу для нахождения диагонали ромба:
Длина диагонали22 = половина длины стороны2 + половина длины стороны2
Длина диагонали22 = 8 см/22 + 8 см/22
Длина диагонали22 = 4 см2 + 4 см2
Длина диагонали22 = 16 см2
Длина диагонали2 = √16 см
Длина диагонали2 = 4 см
Таким образом, длина диагонали ромба в данном примере равна 4 см.
Вы можете использовать эту формулу и следовать тому же шаблону для расчета диагонали ромба в любых других примерах. Помните, что стороны ромба должны быть перпендикулярны диагоналям, чтобы рассматривать его как ромб.