Площадь прямоугольного треугольника – это одна из основных характеристик этой фигуры и используется для решения множества задач. Но как рассчитать ее? Не пугайтесь сложных формул и длинных вычислений. Сегодня мы расскажем вам о простом и быстром способе нахождения площади прямоугольного треугольника, который точно не оставит вас равнодушными. Этот метод подходит даже для тех, кто не очень хорошо знаком с математикой, так что приступим к изучению!
Перед тем, как перейти к расчетам, давайте вспомним основные свойства прямоугольного треугольника. Он имеет один прямой угол (90 градусов) и два острых угла. Сторона, которая прилегает к прямому углу (проекция), называется катетом, а сторона, напротив прямого угла (гипотенуза), является самой длинной. Именно катеты важны для расчета площади треугольника, а теперь мы объясним, почему.
Наш метод основан на простой идеи: площадь прямоугольного треугольника равна половине произведения длин его катетов. Скажем честно, этой формулой легко запомнить и использовать в жизни.
Что такое прямоугольный треугольник
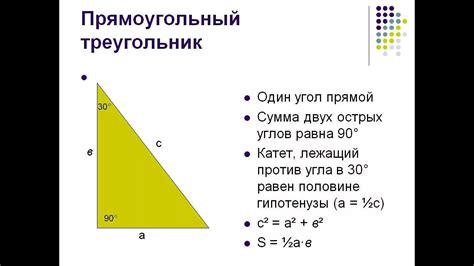
Гипотенуза - это наибольшая сторона прямоугольного треугольника, которая является гипотенузой теоремы Пифагора. Эта теорема утверждает, что квадрат гипотенузы равен сумме квадратов катетов: a^2 + b^2 = c^2, где a и b - катеты, а c - гипотенуза.
Прямоугольные треугольники широко используются в геометрии и находят применение в различных областях, таких как архитектура, инженерия, физика и другие. Знание площади прямоугольного треугольника позволяет решать разнообразные задачи и вычисления, связанные с этой геометрической фигурой.
Как найти гипотенузу прямоугольного треугольника
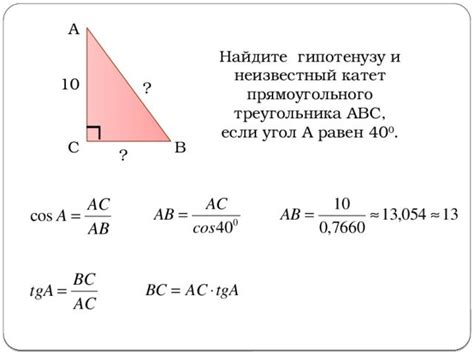
Существует простая формула, позволяющая найти гипотенузу прямоугольного треугольника при известных значениях катетов (других двух сторон треугольника). Эта формула называется теоремой Пифагора.
Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов катетов. Формула записывается следующим образом:
c^2 = a^2 + b^2
Где c - гипотенуза, a и b - катеты.
Для нахождения гипотенузы, необходимо знать значения катетов, затем подставить их в формулу и выполнить несложные математические операции. Прямоугольный треугольник может быть решен на калькуляторе или с использованием программы для работы с геометрией.
Помните, что значения катетов должны быть положительными и больше нуля. Иначе формула будет применяться неправильно.
Как найти катет прямоугольного треугольника
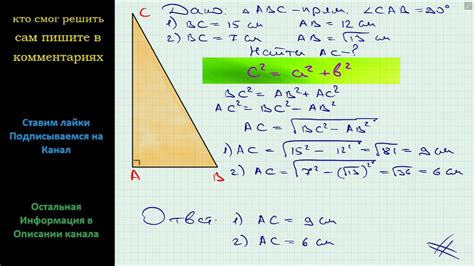
Если известны длины гипотенузы и одного из катетов, можно найти длину второго катета с помощью теоремы Пифагора.
Теорема Пифагора гласит: квадрат длины гипотенузы равен сумме квадратов длин катетов.
Пусть известны длина гипотенузы (c) и длина одного катета (a). Тогда второй катет (b) можно найти по следующей формуле:
b = √(c² - a²)
Пример:
- Длина гипотенузы: 5
- Длина одного катета: 3
Используя формулу, найдем длину второго катета:
b = √(5² - 3²)
b = √(25 - 9)
b = √16
b = 4
Таким образом, второй катет прямоугольного треугольника равен 4.
Помните, что длина катета не может быть отрицательным числом, поэтому при использовании теоремы Пифагора необходимо соблюдать правильный порядок подстановки значений и учитывать ограничения задачи.
Формула для нахождения площади прямоугольного треугольника
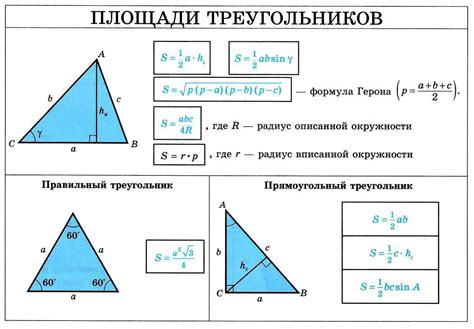
Площадь прямоугольного треугольника может быть найдена с помощью простой формулы. Данная формула основывается на длине катетов треугольника.
Формула для нахождения площади прямоугольного треугольника:
| Формула | Описание |
|---|---|
| S = (a * b) / 2 | где S - площадь треугольника, a и b - длины катетов треугольника |
Для использования данной формулы необходимо знать длины обоих катетов прямоугольного треугольника- его гипотенузы и одного из катетов либо второго катета.
Пример:
Дано прямоугольный треугольник с катетами a = 5 и b = 3. Чтобы найти его площадь, подставим значения a и b в формулу:
S = (5 * 3) / 2 = 7.5
Таким образом, площадь прямоугольного треугольника с катетами 5 и 3 равна 7.5 квадратных единиц.
Пример решения задачи на нахождение площади треугольника
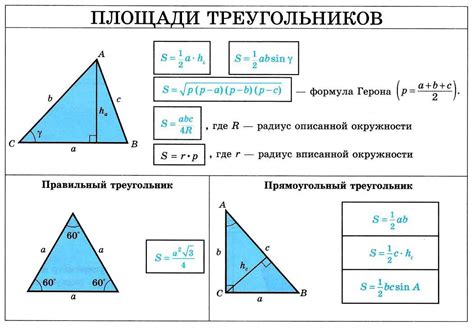
Для начала необходимо знать, что площадь прямоугольного треугольника можно найти по формуле:
S = (a * b) / 2
где S - площадь треугольника, а и b - длины катетов.
Приведем пример решения задачи:
Дан прямоугольный треугольник со сторонами:
- a = 5
- b = 8
Подставим значения a и b в формулу:
S = (5 * 8) / 2
Рассчитаем площадь:
S = 40 / 2
S = 20
Таким образом, площадь прямоугольного треугольника со сторонами 5 и 8 равна 20. Этот метод нахождения площади треугольника прост и быстр.
Построение прямоугольного треугольника с заданной площадью
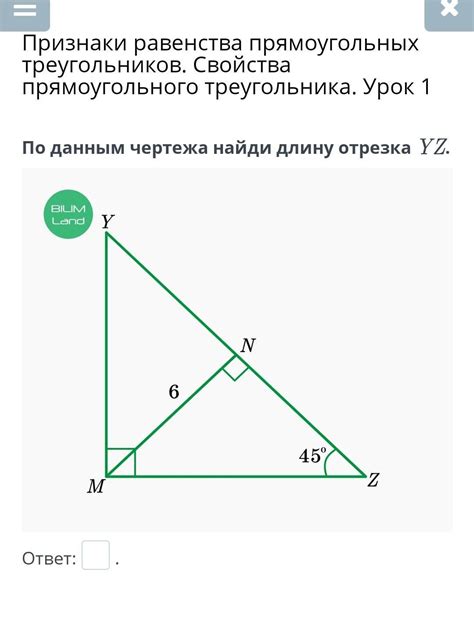
Чтобы построить прямоугольный треугольник с заданной площадью, нужно знать две стороны треугольника и угол между ними. Зная эти данные, можно вычислить третью сторону и построить треугольник.
Для начала, найдите формулу вычисления площади прямоугольного треугольника:
Площадь = (a * b) / 2
где a и b - катеты треугольника, а площадь - искомое значение.
Чтобы построить треугольник, с заданной площадью, нужно знать один из катетов, а также угол между ними. Для этого можно использовать теорему Пифагора:
a2 = c2 - b2
где a - искомый катет, c - гипотенуза, b - другой катет.
Например, если известна площадь треугольника и один катет, можно вычислить второй катет по формуле:
b = √(c2 - a2)
Таким образом, находя катеты треугольника с использованием формул и известной площади, можно построить прямоугольный треугольник с заданной площадью.