Эпсилон – одна из самых известных греческих букв, которая широко используется в математике и физике. Нарисовать ее может показаться сложным заданием, но на самом деле это достаточно просто, если вы знаете некоторые основные правила. В этой статье мы расскажем вам, как нарисовать эпсилон за 5 шагов, даже если вы совсем не умеете рисовать.
Шаг 1. Возьмите лист бумаги и ручку. Начните с рисования вертикальной линии, которая будет служить основой для вашего эпсилона. Убедитесь, что линия достаточно длинная, чтобы вместить в себя остальные элементы буквы.
Шаг 2. Перейдите к рисованию верхней части эпсилона. Для этого сделайте небольшой горизонтальный разрез на линии, не доходя до правого края. Затем возвращайтесь на эту точку и сделайте наклон влево, чтобы создать верхнюю часть буквы. Продолжайте рисовать наклон вниз до основной вертикальной линии.
История символа "эпсилон"

Символ "эпсилон" был изначально использован древнегреческими математиками и философами, такими как Пифагор, как одна из букв для обозначения неизвестных величин и параметров в уравнениях и формулах.
В дальнейшем символ "эпсилон" нашел применение и в других областях науки, включая физику, химию и информатику. Он часто используется для обозначения очень малых величин, близких к нулю, а также для обозначения эпсилон-окрестности при описании математических функций и графиков.
Интересный факт: греческая буква "эпсилон" служит также символом для базовой эпсилон-дельта нотации, используемой для определения пределов функций в математическом анализе.
Символ "эпсилон" имеет важное значение в различных научных областях и олицетворяет понятие малости и приближения в математике и физике.
Что такое "эпсилон"?

В математике эпсилон часто используется для обозначения очень малых или близких к нулю величин. Он применяется, например, при формулировке математических границ, пределов и континуумов. Также эпсилон может использоваться для обозначения погрешностей или степени точности в численных методах и алгоритмах.
В физике эпсилон может обозначать коэффициент диэлектрической проницаемости в материалах. Он указывает на способность материала проводить электрический ток и влиять на электрическое поле.
В информатике эпсилон может использоваться в различных областях, таких как вычислительная геометрия, алгоритмы поиска и оптимизации. Также его можно встретить в теории графов и других разделах компьютерных наук.
Все это делает эпсилон важным символом для понимания и работы с различными научными и математическими концепциями. Оно позволяет нам точно описывать и измерять величины, устанавливать границы и проводить различные анализы.
Шаг 1: Учимся рисовать прямоугольник

- Возьмите линейку и положите ее на лист бумаги или холст.
- Выберите точку A как начальную точку прямоугольника.
- Проведите линию от точки A влево или вправо. Это будет одна из сторон прямоугольника.
- С выбранного конца этой линии проведите еще одну линию вверх или вниз. Теперь у вас две стороны прямоугольника.
- От конца второй линии проведите последнюю линию, чтобы соединить ее с начальной точкой A. Теперь у вас есть законченный прямоугольник!
При рисовании прямоугольника не забывайте использовать линейку для получения ровных и прямых линий. Если вам нужен определенный размер прямоугольника, используйте соответствующие измерения на линейке.
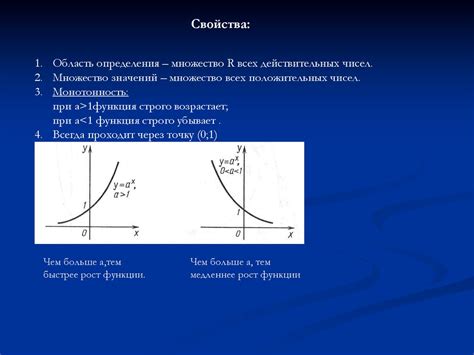
Шаг 2: Новая форма – показательная функция
Для начала создадим новый объект класса Canvas, который будет представлять собой полотно, на котором мы будем рисовать нашу показательную функцию:
Canvas canvas = new Canvas();
Затем, мы можем настроить размеры нашего полотна с помощью методов canvas.setSize(width, height), где width и height – это ширина и высота полотна соответственно:
canvas.setSize(500, 300);
Теперь, чтобы нарисовать показательную функцию, мы должны знать ее математическое определение. Давайте предположим, что у нас есть функция, которая описывает рост количества бактерий в определенной среде в зависимости от времени. Для примера, давайте возьмем функцию вида:
f(t) = a * e^(b * t),
где t – это время, a и b – это константы, определяющие вид функции.
Чтобы нарисовать эту функцию на полотне, нам необходимо проходить по каждой точке функции и рисовать ее на полотне. Для этого мы используем цикл for:
for (int t = 0; t <= 10; t++) {
double y = a * Math.pow(Math.E, b * t); // Вычисляем значение функции в точке t
canvas.drawPoint(t, y); // Рисуем точку на полотне
}
Где t – это переменная, которая будет изменяться от 0 до 10, и y – это значение функции в точке t.
После выполнения цикла, наше полотно будет содержать нарисованную показательную функцию.
Шаг 3: Добавляем левое "крыло"

Теперь переходим к созданию левого "крыла" эпсилон символа. Для этого нарисуем прямую линию, которая будет начинаться из левого верхнего угла вертикальной линии и заканчиваться у основания символа.
Для создания линии можем использовать отрезок вертикальной линии в качестве направляющей.
Пример:
| | | _______ | |
В этом примере левое "крыло" состоит из прямой линии, которая расположена слева от вертикальной линии символа.
После того, как мы добавили левое "крыло", эпсилон символ постепенно принимает свою форму.
Шаг 4: Делаем правую "корзинку"

Чтобы нарисовать правую "корзинку" эпсилона, следуйте этим инструкциям:
1. Начните с прямоугольника, который будет служить основанием "корзинки". Нарисуйте вертикальную линию справа от основания. Это будет задний край "корзинки".
2. Соедините верхний правый угол основания с задним краем вертикальной линией. Это будет правый боковой край "корзинки".
3. Нарисуйте горизонтальную линию над основанием, соединяющую верхнюю часть "корзинки" с задним краем.
4. Добавьте дополнительные небольшие горизонтальные линии под основанием, чтобы создать впечатление "выпирающих" элементов опоры "корзинки".
5. Закончите, добавив несколько небольших вертикальных линий на заднем крае "корзинки", чтобы создать эффект жесткости и объемности.
Теперь ваша правая "корзинка" эпсилона готова!
Шаг 5: Завершаем символ "эпсилон"

Последний шаг завершает наше изображение символа "эпсилон".
Для этого мы проводим горизонтальную черту в нижней части символа. Чтобы сделать ее, начните с правой части круга, который мы нарисовали в предыдущем шаге, и проведите линию влево до левой части круга, а затем вправо до правой части круга. Это даст нам нижнюю часть символа "эпсилон".
У нашего символа "эпсилон" теперь есть все необходимые детали. Вы можете закончить его, добавив тонкие черные контуры вдоль линий, чтобы они выглядели более четкими и завершенными.
Поздравляю! Теперь вы знаете, как нарисовать символ "эпсилон" всего за 5 шагов.