Понимание, как находить отношение площади четырехугольника к площади треугольника, может быть полезным в различных областях, включая геометрию, строительство и дизайн. Этот метод расчета является довольно простым и может быть выполнен шаг за шагом без необходимости использовать сложные формулы или специальное оборудование.

Первый шаг в процессе нахождения отношения площадей четырехугольника к треугольнику - это измерение сторон этих фигур. Для четырехугольника требуется измерить длины всех его сторон, а треугольника - двух его сторон. Важно убедиться, что измерения проведены с высокой точностью, чтобы получить правильный результат.

После измерения сторон необходимо найти высоту треугольника. Для этого используется прямая, перпендикулярная одной из сторон треугольника и проходящая через вершину, которая не является концом этой стороны. Длина этой прямой будет являться высотой треугольника. Измерение ее дает нам важную информацию для последующих расчетов.

Зная длины сторон и высоту треугольника, можно приступить к вычислению площадей. Площадь треугольника рассчитывается по формуле: S = 0.5 * a * h, где S - площадь, a - длина одной стороны треугольника, h - высота треугольника. Площадь четырехугольника рассчитывается по формуле разбиения его на два треугольника и суммирования их площадей.

Окончательный шаг - нахождение отношения площади четырехугольника к площади треугольника. Для этого необходимо разделить площадь четырехугольника на площадь треугольника. Полученное число будет являться искомым отношением. Например, если площадь четырехугольника равна 10 квадратным единицам, а площадь треугольника - 5 квадратным единицам, то отношение будет равно 2.

Нахождение отношения площадей четырехугольника к треугольнику

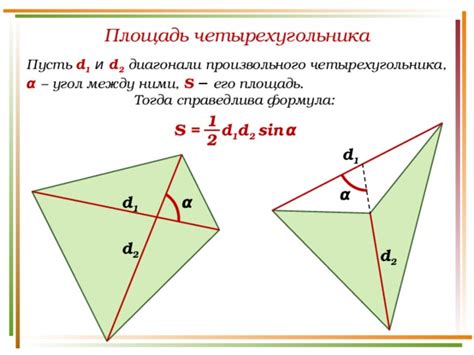
Чтобы найти отношение площадей четырехугольника к треугольнику, нужно выполнить следующие шаги:

1. Найдите площадь четырехугольника. Для этого можно воспользоваться различными методами, такими как формула Герона для треугольника или формула площади трапеции, если четырехугольник является трапецией.
2. Найдите площадь треугольника, который образован одной стороной четырехугольника и диагональю, пересекающей эту сторону. Для этого можно использовать формулу площади треугольника, в которой известны основание (сторона четырехугольника) и высота (диагональ).
3. Поделите площадь четырехугольника на площадь треугольника, чтобы найти отношение площадей.

Результатом будет число, которое представляет отношение площадей четырехугольника к треугольнику.

Найти отношение площадей четырехугольника к треугольнику может быть полезно при решении различных геометрических или физических задач, например, при расчете площади пространства между двумя поверхностями или при определении плотности распределения материала.

Определение площадей фигур

1. Определение площади четырехугольника:
   • Измерьте длины всех сторон четырехугольника и запишите их значения.
   • Разделите четырехугольник на два треугольника, соединив диагонали.
   • Используя формулу площади треугольника (полуобъем), рассчитайте площади обоих треугольников.
   • Сложите полученные значения площадей треугольников, чтобы найти общую площадь четырехугольника.
2. Определение площади треугольника:
   • Измерьте длины основания и высоты треугольника и запишите их значения.
   • Умножьте длину основания на высоту и разделите полученное значение на 2.
   • Полученное число представляет площадь треугольника в единицах измерения.

После определения площадей фигур, можно вычислять их отношение. Отношение площадей четырехугольника к треугольнику можно найти, разделив площадь четырехугольника на площадь треугольника.

Описание простого метода расчета

Для расчета отношения площадей четырехугольника к треугольнику используется простой метод, который включает несколько шагов:

1. Найдите высоту треугольника, проведя перпендикуляр из вершины треугольника к противоположной стороне. Это можно сделать с помощью геометрической конструкции или используя формулу высоты треугольника.
2. Вычислите площадь треугольника, умножив его высоту на длину одной из его сторон и разделив полученное значение на 2.
3. Найдите площадь четырехугольника. Для этого разбейте его на два треугольника, проведя диагональ, и вычислите площадь каждого треугольника по формуле, описанной в предыдущем шаге.
4. Найдите отношение площадей, разделив площадь четырехугольника на площадь треугольника.

Таким образом, простой метод расчета отношения площадей четырехугольника к треугольнику позволяет получить точную численную характеристику их соотношения.

Постановка задачи на примере конкретного четырехугольника и треугольника

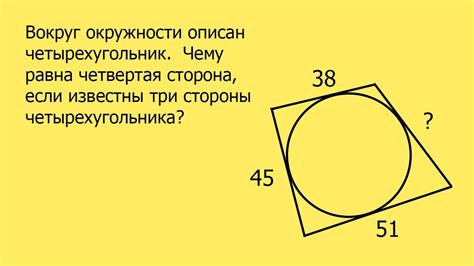
Для начала, нам нужно найти площади обеих фигур. Чтобы найти площадь четырехугольника ABCD, мы можем использовать формулу площади треугольника. Мы разобьем четырехугольник ABCD на два треугольника: ABC и ACD. Затем мы найдем площади обоих треугольников, используя формулу площади треугольника, которая составляет половину от произведения длины основания на высоту. После этого мы сложим площади треугольников ABC и ACD, чтобы получить площадь всего четырехугольника ABCD.

Для нахождения площади треугольника DEF мы также можем использовать формулу площади треугольника, примененную к сторонам треугольника DEF.

После того, как мы найдем площади обоих фигур, мы можем поделить площадь четырехугольника ABCD на площадь треугольника DEF, чтобы получить отношение площадей этих фигур.

Таким образом, мы можем использовать данную пошаговую инструкцию для решения любой задачи по нахождению отношения площадей четырехугольника к треугольнику с применением простого метода расчета.

Расчет площадей фигур по формулам или правилам

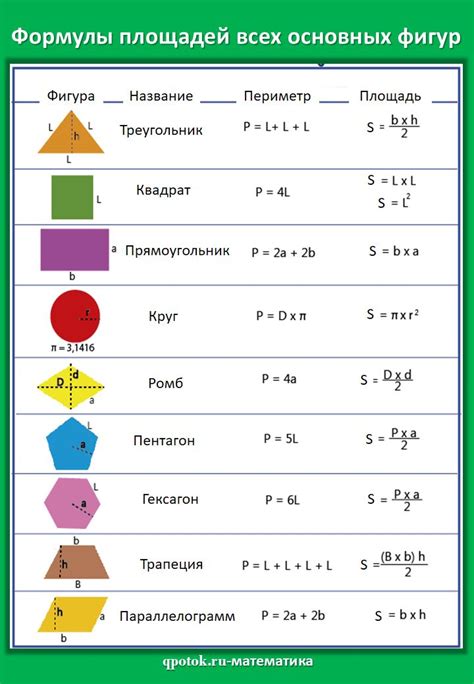
Для расчета площади различных геометрических фигур существует ряд формул и правил, которые позволяют получить точные результаты. В данном контексте мы рассмотрим простой метод расчета отношения площадей четырехугольника к треугольнику.

Для начала, нам понадобятся следующие данные:

• Стороны четырехугольника (AB, BC, CD, DA)
• Высота треугольника, проведенная из одного из углов четырехугольника (h)
• Длины оснований треугольника (BC, CD)

По этим данным мы можем применить следующие формулы:

1. Площадь треугольника ABC = (BC * h) / 2
2. Площадь треугольника ACD = (CD * h) / 2
3. Площадь четырехугольника ABCD = площадь треугольника ABC + площадь треугольника ACD

После рассчета площадей по указанным формулам, необходимо сложить полученные значения для получения окончательного результата.

Таким образом, следуя этим простым шагам, вы сможете легко рассчитать отношение площадей четырехугольника к треугольнику.

Определение отношения площадей четырехугольника к треугольнику и его интерпретация

Для определения отношения площадей четырехугольника к треугольнику существует простой метод расчета. Рассмотрим его шаги по порядку.

Шаг 1: Возьмите четырехугольник и треугольник, для которых вы хотите найти отношение площадей. Пусть площадь четырехугольника будет обозначена как S_{четырехугольник}, а площадь треугольника - как S_{треугольник}.

Шаг 2: Определите длины всех сторон четырехугольника и треугольника. Необходимо знать значения всех сторон, чтобы впоследствии можно было вычислить площади фигур.

Шаг 3: Используя формулу Герона, найдите площадь треугольника. Формула Герона имеет следующий вид:

S_{треугольник} = √(p * (p - a) * (p - b) * (p - c))

где a, b и c - длины сторон треугольника, а p - полупериметр треугольника, определяемый по формуле:

p = (a + b + c) / 2

Шаг 4: Разведите формулу площади четырехугольника на две формулы площади треугольника. Зная, что четырехугольник может быть разделен на два треугольника, мы можем записать площадь четырехугольника как сумму площадей этих двух треугольников:

S_{четырехугольник} = S_{треугольник 1} + S_{треугольник 2}

Шаг 5: Подставьте найденные значения площади треугольника и площади четырехугольника в формулу отношения:

Отношение площадей = S_{четырехугольник} / S_{треугольник}

Шаг 6: В полученном результате интерпретируйте отношение площадей. Если отношение меньше 1, это означает, что площадь четырехугольника меньше площади треугольника. Если отношение больше 1, это означает, что площадь четырехугольника больше площади треугольника. Если отношение равно 1, это означает, что площади обоих фигур равны.

Таким образом, следуя этой пошаговой инструкции, вы сможете определить отношение площадей четырехугольника к треугольнику и правильно его интерпретировать.