Куб - одно из простейших геометрических тел, имеющих ребра одинаковой длины и параллельные грани. Однако, задача нахождения сечения куба по трем произвольным точкам может показаться сложной. Она требует не только хорошего математического аппарата, но и навыков в алгоритмическом мышлении.

Для нахождения сечения куба по трем точкам можно использовать несколько методов. Один из самых простых и быстрых - метод плоскости. Этот метод основан на принципе, что три точки определяют плоскость, в которой будет находиться сечение куба.

Сначала необходимо вычислить векторы направления ребер куба, заданных тремя точками. Затем, используя эти векторы, построить уравнение плоскости, проходящей через эти три точки. Далее, для каждой грани куба проверить, лежит ли она в этой плоскости.

Таким образом, нахождение сечения куба по трем точкам является задачей решаемой с использованием простых геометрических и алгебраических методов. Используя описанный выше метод плоскости, можно быстро и эффективно решить данную задачу.

Как найти сечение куба

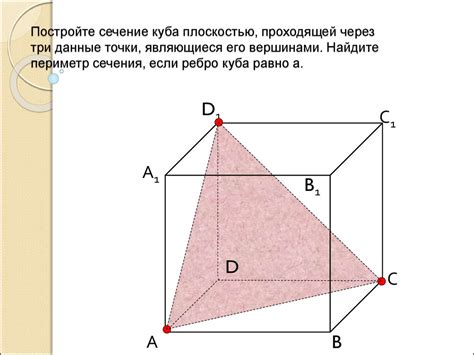
Сечение куба может быть найдено с помощью трёх точек, которые лежат на его поверхности. Для этого необходимо выполнить следующие шаги:

1. Определить координаты данных трёх точек на поверхности куба.
2. Построить плоскость, проходящую через эти точки. Для этого можно использовать формулу плоскости, она задаётся уравнением ax + by + cz + d = 0.
3. Найти точки пересечения этой плоскости с рёбрами куба.

Таким образом, мы можем найти сечение куба с помощью трёх точек, которые лежат на его поверхности. Этот метод позволяет быстро и просто решить данную задачу.

Быстрый способ

Шаг 1: Определите координаты трех точек, через которые должно пройти сечение куба. Обозначим их как A, B и C.

Шаг 2: Для нахождения плоскости, содержащей сечение, воспользуйтесь векторным произведением векторов AB и AC. Представим эти векторы следующим образом:

AB = (x_B - x_A, y_B - y_A, z_B - z_A)

AC = (x_C - x_A, y_C - y_A, z_C - z_A)

Шаг 3: Найдите векторное произведение векторов AB и AC:

N = AB × AC = (n_x, n_y, n_z)

Шаг 4: Зная нормальный вектор плоскости сечения, выразите уравнение плоскости вида:

nx * (x - x₀) + ny * (y - y₀) + nz * (z - z₀) = 0,

где (x₀, y₀, z₀) - координаты любой точки, через которую проходит плоскость. Для нахождения координаты такой точки можно выбрать одну из трех исходных точек.

Шаг 5: Теперь у вас есть уравнение плоскости, содержащей сечение куба. Можно проверить, пересекаются ли ребра куба с этой плоскостью, путем подстановки координат вершин куба в уравнение плоскости и определения знаков выражения.