Формула Герона – это один из самых известных и простых способов нахождения площади треугольника. Она основывается на длинах его сторон и позволяет с высокой точностью определить площадь фигуры без необходимости знать высоту или углы. Формула Герона является классическим примером применения математических алгоритмов для решения практических задач.
Найдем площадь треугольника по формуле Герона:
Для этого нужно знать длину всех трех его сторон: a, b и c. Далее, используя формулу:
площадь = корень квадратный из (p * (p - a) * (p - b) * (p - c)),
где p – полупериметр треугольника, равный сумме длин его сторон, поделив на 2.
Важно отметить, что для использования формулы Герона необходимо, чтобы треугольник был неравнобедренным или неравносторонним.
Преимущества использования формулы Герона

| 1. | Простота использования. |
| 2. | Быстрота расчетов. |
| 3. | Точность результатов. |
| 4. | Использование только длин сторон треугольника. |
Основным преимуществом формулы Герона является ее простота использования. Для расчета площади треугольника по этой формуле необходимо знать длины всех его сторон. Затем достаточно подставить значения сторон в формулу и выполнить несколько арифметических операций.
Следующим преимуществом формулы Герона является скорость расчетов. Поскольку эта формула является простой и непрерывной, ее применение не требует большого количества вычислительных операций. Это позволяет получить результаты быстро и без лишних затрат времени и ресурсов.
Еще одним важным преимуществом формулы Герона является ее высокая точность. При правильном использовании формулы и точных измерениях сторон треугольника, результат расчета площади будет близким к точному значению. Это делает формулу Герона надежным и полезным инструментом при работе с треугольниками.
Наконец, использование только длин сторон треугольника является еще одним преимуществом формулы Герона. В отличие от других методов, которые требуют знания дополнительных параметров, например углов или высоты, формула Герона позволяет найти площадь только по длинам сторон. Это делает использование формулы Герона более удобным и доступным для широкого круга задач.
Что такое формула Герона и как она работает?

Формула Герона основывается на полупериметре треугольника, который вычисляется как сумма длин всех трех его сторон, деленная на 2. Используя полупериметр, формула Герона вычисляет площадь треугольника по следующей формуле:
S = √(p * (p - a) * (p - b) * (p - c))
где S - площадь треугольника, p - полупериметр треугольника, a, b и c - длины его сторон.
Процесс вычисления площади треугольника с использованием формулы Герона упрощается следующим образом:
- Найти длины сторон треугольника.
- Вычислить полупериметр треугольника.
- Подставить значения в формулу Герона.
- Извлечь квадратный корень из полученного значения для получения площади треугольника.
Таким образом, формула Герона позволяет нам легко и быстро вычислить площадь треугольника по длинам его сторон, без необходимости знать его высоту или используя другие методы.
Шаги для расчета площади треугольника по формуле Герона
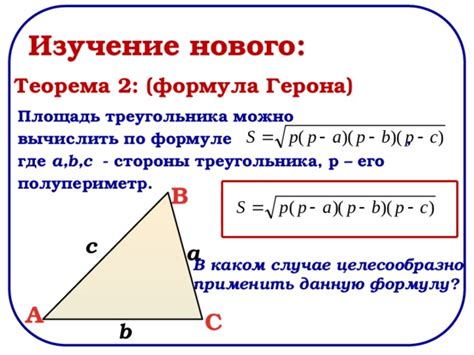
Для расчета площади треугольника по формуле Герона необходимо выполнить следующие шаги:
1. Измерьте длину каждой стороны треугольника с помощью линейки или другого инструмента.
2. Обозначьте длины сторон треугольника как a, b и c.
3. Используя полученные значения, вычислите полупериметр треугольника по формуле:
p = (a + b + c) / 2
где p - полупериметр.
4. Далее, используя значения сторон треугольника и полупериметр, вычислите площадь треугольника по формуле Герона:
S = √(p · (p - a) · (p - b) · (p - c))
где S - площадь треугольника.
5. Вычислите значение выражения под знаком корня, умножив полупериметр на разность между полупериметром и каждой из сторон треугольника.
6. Найдите квадратный корень из полученного значения, чтобы получить площадь треугольника.
Теперь вы знаете, как рассчитать площадь треугольника по формуле Герона!
Примеры использования формулы Герона

Пример 1:
Пусть у нас есть треугольник со сторонами длиной a = 5, b = 4 и c = 3. Мы можем использовать формулу Герона для вычисления его площади.
Сначала найдем полупериметр треугольника:
сумма всех сторон / 2 = (5 + 4 + 3) / 2 = 6.
Теперь используем формулу Герона:
площадь = квадратный корень из (6 * (6-5) * (6-4) * (6-3)) = 6.
Таким образом, площадь треугольника равна 6.
Пример 2:
Допустим, у нас есть треугольник со сторонами длиной a = 7, b = 8 и c = 10. Также нам известен угол между сторонами a и b, равный 45 градусов. Как найти его площадь с использованием формулы Герона?
Сначала найдем полупериметр:
сумма всех сторон / 2 = (7 + 8 + 10) / 2 = 12.5.
Теперь используем формулу Герона:
площадь = квадратный корень из (12.5 * (12.5-7) * (12.5-8) * (12.5-10)) = 27.386.
Таким образом, площадь треугольника равна примерно 27.386 квадратных единиц.
Пример 3:
Пусть у нас есть треугольник с неизвестными сторонами a, b и c, но известными его высота h и основание b. Мы можем использовать формулу Герона для вычисления площади.
Сначала найдем сторону a с помощью теоремы Пифагора:
a = квадратный корень из (c^2 - h^2).
Теперь используем формулу Герона:
площадь = квадратный корень из (4 * a * b * (a+b-c)) / 4.
Таким образом, мы можем найти площадь треугольника, используя известные значения высоты и основания, а также найденную сторону a.
Формула Герона является мощным инструментом, позволяющим вычислять площадь треугольника, даже если известны только значения его сторон или некоторые из его углов. Она широко применяется в геометрии и других областях, где требуется вычисление площади треугольников.
Советы по использованию формулы Герона для расчета площади треугольника:
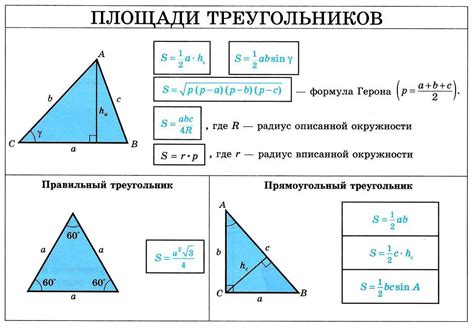
| 1. Запишите длины сторон: | Прежде чем начать использовать формулу Герона, убедитесь, что у вас есть точные измерения длин всех трех сторон треугольника. Запишите эти значения, чтобы потом не запутаться. |
| 2. Используйте формулу: | Формула Герона для расчета площади треугольника выглядит следующим образом: |
| |
Где S - площадь треугольника, p - полупериметр треугольника (p = (a + b + c) / 2), а a, b и c - длины сторон. | |
| 3. Посчитайте площадь: | Подставьте значения длин сторон треугольника в формулу Герона и выполните необходимые математические операции. В результате получите площадь треугольника. Не забудьте извлечь квадратный корень из полученного значения. |
| 4. Проверьте ответ: | После получения значения площади треугольника с помощью формулы Герона, рекомендуется проверить его с помощью других методов расчета площади треугольника. Это поможет вам убедиться в правильности результата. |
Использование формулы Герона для расчета площади треугольника - это быстрый и надежный способ получить точный результат. Следуя этим советам, вы сможете легко и верно применить эту формулу в практике.
Возможные проблемы и ошибки при использовании формулы Герона
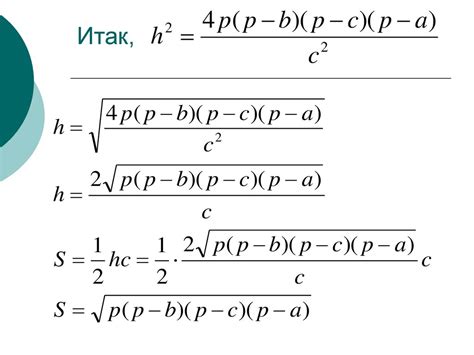
При использовании формулы Герона для вычисления площади треугольника могут возникнуть следующие проблемы и ошибки:
- Неверные значения сторон треугольника: Если вводимые значения сторон треугольника некорректны (например, отрицательные числа или нули), то результат вычисления площади будет неверным. Перед использованием формулы необходимо убедиться, что введенные значения являются положительными и отличными от нуля.
- Неправильное расположение вершин треугольника: Если вершины треугольника заданы неправильно или не в правильном порядке, то результат вычисления площади также будет неверным. Формула Герона предполагает, что вершины треугольника заданы в порядке обхода по или против часовой стрелки. Убедитесь, что вершины треугольника заданы правильно.
- Отсутствие проверки существования треугольника: Формула Герона может использоваться только для вычисления площади треугольника. Если заданные значения сторон не могут образовать треугольник (например, когда сумма двух сторон меньше третьей), то результат будет недействительным. Перед использованием формулы необходимо проверить, что заданные значения сторон образуют треугольник.
- Округление значений: При использовании формулы Герона может возникнуть проблема с округлением значений. Если округление проводится слишком рано или слишком поздно, результаты могут быть неточными или существенно отличаться от ожидаемых. Рекомендуется хранить промежуточные значения с большей точностью и округлять результат только в конце вычислений.
Помимо этих возможных проблем, также необходимо учесть особенности данной формулы при вычислении площади треугольника. Всегда важно следить за правильностью вводимых данных, чтобы избежать возможных ошибок и получить точный результат.