Прямая призма - это геометрическое тело с двумя основаниями, которые являются параллелограммами, и боковыми гранями, которые представляют собой прямоугольники или квадраты
.
Основания призмы могут быть разных размеров и форм, и для рассчетов может потребоваться найти диагональ одного из них. Это важно, например, при вычислении объема призмы или ее площади поверхности.
Формула для нахождения диагонали основания прямой призмы зависит от формы основания. Если основание является параллелограммом, то диагональ можно найти с помощью теоремы Пифагора.
Что такое диагональ основания?

Диагональ основания является одной из важных характеристик прямой призмы, поскольку она определяет ее геометрические свойства и позволяет находить различные показатели призмы, такие как объем или площадь поверхности.
Чтобы найти диагональ основания прямой призмы, необходимо знать длину сторон основания и расстояние между противоположными вершинами основания. Нахождение диагонали основания может быть полезным при решении различных задач геометрии или при конструировании объектов, связанных с прямыми призмами.
Диагональ основания прямой призмы может быть найдена с использованием теоремы Пифагора или других соотношений между сторонами треугольников. Зная формулы и правила для вычисления диагонали основания, можно более точно определить геометрические характеристики призмы и использовать их в различных прикладных задачах.
Как находить диагональ основания?

Для определения диагонали основания прямой призмы, нужно знать длину одной из сторон основания и высоту призмы. Формула для вычисления диагонали имеет вид:
Диагональ = √(длина стороны основания^2 + высота^2)
Где:
- Диагональ – длина диагонали основания призмы;
- длина стороны основания – длина любой стороны основания призмы;
- высота – высота призмы, расстояние между основаниями.
По этой формуле можно вычислить диагональ основания для любой прямой призмы, если известны значения стороны основания и высоты. Учитывайте единицы измерения при подстановке значений в формулу, так как диагональ будет иметь такую же единицу измерения, как сторона основания.
Важно: диагональ основания необходимо отличать от диагонали призмы, которая соединяет две противоположные вершины призмы.
Простое объяснение нахождения диагонали основания прямой призмы

Для того чтобы найти диагональ основания прямой призмы, необходимо знать длины ребра и высоты призмы. Зная эти данные, применяется теорема Пифагора.
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Применяя эту теорему к прямоугольному треугольнику, состоящему из диагонали основания, ребра и половины высоты призмы, получаем следующую формулу:
Диагональ^2 = Ребро^2 + (Высота/2)^2
Для получения значения диагонали основания прямой призмы достаточно подставить известные значения ребра и высоты в эту формулу и произвести несложные математические вычисления.
Практическое применение нахождения диагонали основания
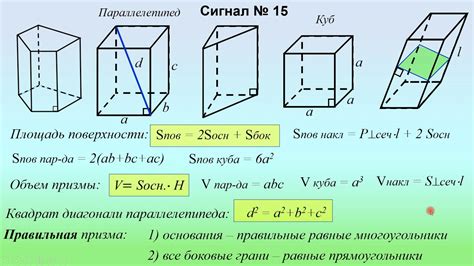
Расчет диагонали основания прямой призмы имеет ряд практических применений в различных областях. Ниже приведены некоторые из них:
- Строительство: Нахождение диагонали основания может быть полезным при проектировании зданий. Например, при строительстве крыши или фундамента необходимо знать длину диагонали, чтобы точно распределить нагрузку на конструкцию.
- Дизайн интерьера: При проектировании интерьера может быть важно знать длину диагонали основания прямой призмы, например, при расстановке мебели или расчете необходимого пространства для размещения предметов.
- Изготовление мебели: При изготовлении мебели, такой как стол или стеллаж, важно знать диагональ основания, чтобы правильно распределить нагрузку на конструкцию и обеспечить ее прочность.
- Архитектура: В архитектуре, при проектировании зданий или архитектурных сооружений, знание диагонали основания прямой призмы может быть важным для правильного распределения нагрузки и обеспечения устойчивости конструкции.
- Производство упаковки: В производстве упаковки знание диагонали основания прямой призмы может быть полезным для правильного подбора размеров коробки или контейнера.
Все эти практические применения подчеркивают важность расчета диагонали основания прямой призмы и демонстрируют его широкое использование в различных областях.
Доказательство формулы нахождения диагонали основания
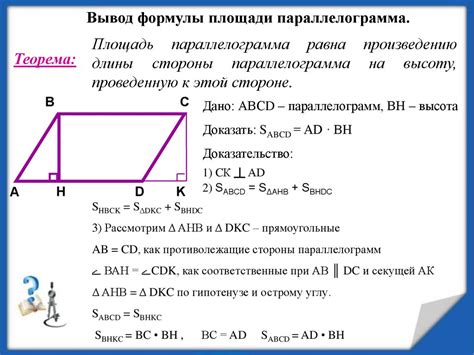
Пусть d - диагональ основания. Тогда в прямоугольном треугольнике, образованном a, b и d, по теореме Пифагора имеет место равенство:
a^2 + b^2 = d^2
Используя это равенство, мы можем выразить диагональ основания по формуле:
d = sqrt(a^2 + b^2)
Таким образом, мы получили формулу для нахождения диагонали основания прямой призмы, основанную на теореме Пифагора.
Формула нахождения диагонали основания призмы

Для нахождения диагонали основания призмы необходимо знать две величины: длину ребра основания и высоту призмы. Формула для расчета диагонали основания призмы будет выглядеть следующим образом:
d = √(а² + h²)
Где:
d - диагональ основания призмы,
а - длина ребра основания,
h - высота призмы.
Пример использования формулы: пусть длина ребра основания призмы равна 4 см, а высота призмы составляет 6 см. Ответ можно получить, подставив значения в формулу:
d = √(4² + 6²) ≈ √(16 + 36) ≈ √52 ≈ 7.2 см
Таким образом, диагональ основания призмы составляет примерно 7.2 см.
Примеры решения задач с нахождением диагонали основания

Для нахождения диагонали основания прямой призмы используется формула, которая основывается на знании значения боковой грани и высоты призмы. Рассмотрим несколько примеров решения задач с нахождением диагонали основания:
Пример 1:
Дана прямая призма, у которой боковая грань равна 6 см, а высота призмы равна 8 см. Найдем диагональ основания.
| Величина | Значение |
|---|---|
| Боковая грань (a) | 6 см |
| Высота (h) | 8 см |
Для нахождения диагонали основания прямой призмы воспользуемся формулой:
Подставим известные значения в формулу:
| d | = | 2 * √(a2 + h2) | |
| = | 2 * √(62 + 82) | ||
| = | 2 * √(36 + 64) | ||
| = | 2 * √100 | ||
| = | 2 * 10 | ||
| = | 20 см |
Таким образом, длина диагонали основания прямой призмы равна 20 см.
Пример 2:
Дана прямая призма, у которой боковая грань равна 10 м, а высота призмы равна 12 м. Найдем диагональ основания.
| Величина | Значение |
|---|---|
| Боковая грань (a) | 10 м |
| Высота (h) | 12 м |
Используем формулу для нахождения диагонали основания:
Подставим известные значения в формулу:
| d | = | 2 * √(a2 + h2) | |
| = | 2 * √(102 + 122) | ||
| = | 2 * √(100 + 144) | ||
| = | 2 * √244 | ||
| = | 2 * 15.62 | ||
| = | 31.24 м |
Таким образом, длина диагонали основания прямой призмы равна 31.24 м.
