Нахождение наибольшего общего делителя является одной из базовых математических навыков, которым обучают в школе. Общий делитель - это число, которое делит два или более числа без остатка. Найти наибольший общий делитель очень важно, так как он позволяет упростить дроби, узнать возможные пропорции и решить множество других задач.
В 6 классе ученики начинают изучать методы нахождения наибольшего общего делителя. Существует несколько методов, но один из самых простых и популярных - это метод деления.
Как использовать метод деления для нахождения наибольшего общего делителя? Прежде всего, необходимо выбрать два числа, для которых нужно найти наибольший общий делитель. Затем следует разделить большее число на меньшее. Если результат деления не является целым числом, то необходимо повторить деление, использовав остаток от предыдущего деления в качестве делителя. Продолжайте делить до тех пор, пока не получите целое число.
Что такое наибольший общий делитель?

Для примера, возьмем числа 12 и 18. Чтобы найти их НОД, необходимо перечислить все их делители и найти наибольший общий делитель. Делители числа 12: 1, 2, 3, 4, 6, 12. Делители числа 18: 1, 2, 3, 6, 9, 18. Наибольший делитель, который присутствует в обоих списках, равен 6. Таким образом, НОД чисел 12 и 18 равен 6.
Наибольший общий делитель широко используется в различных областях, включая теорию чисел, алгебру и криптографию. Он является важным понятием в решении задач, связанных с дробями, линейными уравнениями и многими другими математическими операциями.
Но как найти НОД чисел? Существует несколько методов для нахождения НОД, такие как метод простых делителей, метод Евклида и метод факторизации. В 6 классе вы будете ознакомлены с методом простых делителей, который позволяет найти НОД путем факторизации чисел на простые множители и сравнения их степеней.
НОД является основой для многих математических операций, поэтому понимание его понятия и способа нахождения является важным шагом в вашем математическом образовании.
Определение и примеры

Определить НОД можно с помощью различных методов, но один из самых простых способов - это разложение чисел на простые множители и нахождение их общих множителей.
Рассмотрим пример. Пусть нам нужно найти НОД чисел 24 и 36.
| Числа | Простые множители |
|---|---|
| 24 | 2 * 2 * 2 * 3 |
| 36 | 2 * 2 * 3 * 3 |
Общие простые множители для чисел 24 и 36: 2 и 3.
Наибольший общий делитель равен произведению этих общих множителей: 2 * 3 = 6.
Таким образом, НОД чисел 24 и 36 равен 6.
Как найти наибольший общий делитель двух чисел?

Существует несколько способов нахождения НОД двух чисел. Один из таких способов - метод Евклида. Данный метод основан на простой итеративной процедуре деления одного числа на другое с получением остатка до тех пор, пока остаток не станет равным нулю. При этом НОД будет равен последнему ненулевому остатку.
Пример:
Для нахождения НОД чисел 12 и 18, мы начинаем с деления 18 на 12 с получением остатка 6. Затем делим 12 на 6 с получением остатка 0. Наш последний ненулевой остаток равен 6, следовательно, НОД чисел 12 и 18 равен 6.
Определение НОД может быть полезным при сокращении дробей, решении задач на разложение чисел на простые множители, а также во многих других математических и практических ситуациях.
Метод Евклида

Принцип работы метода Евклида основан на делении одного числа на другое и использовании остатка от деления. Начинается алгоритм с двух чисел, для которых мы хотим найти НОД. Если одно из чисел равно нулю, то НОД будет равен другому числу. Если оба числа не равны нулю, мы делим большее число на меньшее и записываем остаток. Затем повторяем этот процесс, но на этот раз делим меньшее число на остаток. Процесс повторяется до тех пор, пока не получим остаток равный нулю.
Применяя метод Евклида, мы можем эффективно находить НОД для любых чисел. Этот алгоритм является общепризнанным и используется не только в математике, но и в других областях, таких как информатика и криптография.
| Пример: | НОД |
|---|---|
| 12 | 18 |
| 18 % 12 = 6 | 6 |
| 12 % 6 = 0 | 6 |
В приведенном примере мы находим НОД для чисел 12 и 18. Мы начинаем с деления 18 на 12 и получаем остаток 6. Затем мы делим 12 на 6 и получаем остаток 0. Таким образом, наибольший общий делитель чисел 12 и 18 равен 6.
Метод Евклида является одной из базовых математических техник, которая помогает нам находить наибольший общий делитель двух чисел. Он может быть полезен в решении различных задач, таких как упрощение дробей, проверка на простоту чисел и другие.
Пример вычисления НОД
1. Разложим оба числа на простые множители:
24 = 2 × 2 × 2 × 3
36 = 2 × 2 × 3 × 3
2. Выделим все общие простые множители и умножим их друг на друга:
Общие простые множители: 2, 2, 3
2 × 2 × 3 = 12
3. Получили, что НОД чисел 24 и 36 равен 12. То есть 12 является наибольшим числом, которое одновременно делит 24 и 36 без остатка.
Это простой пример вычисления НОД двух чисел. Теперь, имея этот алгоритм, вы можете применить его к другим числам и найти их НОД. Удачи в изучении математики!
Алгоритм поиска НОД чисел с помощью цикла
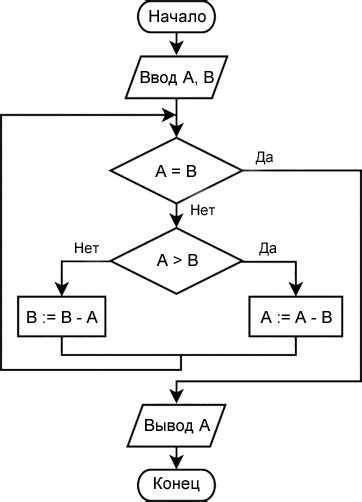
Для начала необходимо выбрать два числа, для которых мы ищем НОД. Для примера, возьмем числа 36 и 48.
В алгоритме с помощью цикла мы будем последовательно проверять, делится ли наше первое число на все числа от 1 до меньшего из двух исходных чисел. Если деление на какое-то число произойдет без остатка, это число станет нашим текущим НОД.
| Шаг | Число | Делится на |
|---|---|---|
| 1 | 36 | 1, 2, 3, 4, 6, 9, 12, 18 |
| 2 | 48 | 1, 2, 3, 4, 6, 8, 12, 16, 24 |
| 3 | 36 | 1, 2, 3, 4, 6, 9, 12, 18 |
| 4 | ... | ... |
В нашем примере НОД чисел 36 и 48 равен 12.
Таким образом, алгоритм поиска НОД чисел с помощью цикла предлагает постепенно проверять все числа от 1 до меньшего из двух исходных чисел. При обнаружении числа, на которое оба числа делятся без остатка, это число становится НОДом.
Задачи на нахождение НОД

- Упрощение дробей: для сокращения дроби до несократимого вида нужно найти НОД числителя и знаменателя, а затем разделить каждое из них на этот НОД.
- Нахождение общих множителей: для поиска общих делителей нескольких чисел нужно найти НОД каждой пары чисел и составить список полученных НОД-ов.
- Вычисление наименьшего общего кратного (НОК): НОК двух чисел можно найти, используя формулу НОК(a,b) = (a*b) / НОД(a,b).
- Решение задач на пропорциональность: при анализе пропорций и поиске неизвестного значения, можно использовать НОД для нахождения соотношений между числами.
Понимание и умение применять НОД в решении задач является важным шагом в изучении математики и развитии логического мышления. Решение задач на нахождение НОД помогает студентам развивать навыки анализа, логического мышления и решения проблем, которые могут быть использованы в различных областях жизни.