В математике предел функции является одной из важнейших концепций, позволяющей изучать и описывать поведение функции на бесконечно удалённых точках. Среди всех пределов функций первый замечательный предел занимает особое место. Он называется "пределом при х стремящемся к нулю". В данной статье мы рассмотрим, как работает этот замечательный предел и почему он так важен в анализе функций.
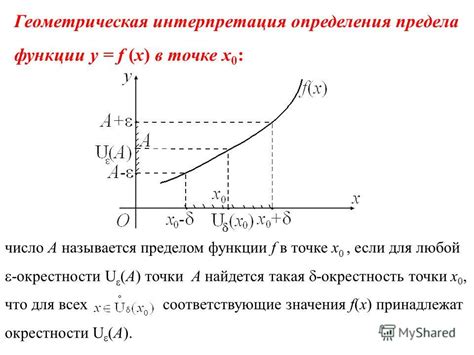
Для начала давайте вспомним определение предела функции. Пусть есть функция f(x) и точка a. Говорят, что предел функции f(x) при x стремящемся к a равен числу L, если для любого положительном числа ε существует такое положительное число δ, что для любого x из промежутка (a-δ, a+δ), отличного от a, значения f(x) лежат в пределах ε от числа L. Формально это записывается так: если |f(x) - L| < ε для всех x из промежутка (a-δ, a+δ), где δ > 0.
Теперь вернёмся к первому замечательному пределу. Он рассматривает предел функции при x стремящемся к нулю. Интересно то, что мы не привязываемся к определённому значению a, а рассматриваем предел на всей числовой оси. Благодаря этому, первый замечательный предел используется для анализа поведения функций в окрестности нуля. Он позволяет исследовать особенности функции и определить, сходится ли она к определённому значению вблизи нуля или расходится. Таким образом, первый замечательный предел является мощным инструментом в исследовании функций и нахожении их особых точек.
Определение предела функции
lim₁→₀ f(x) = L
Здесь символом lim₁→₀ обозначается "предел функции при x, стремящемся к x₀". Число L является пределом функции f(x) в точке x₀.
Предел функции можно определить как по значению, стремящемуся к конечному числу, так и по значению, стремящемуся к бесконечности. В случае стремления к бесконечности используется специальный символ ∞ (бесконечность).
Знание и умение работать с пределами функций позволяет анализировать поведение функций на бесконечности, находить точки разрыва и асимптоты, а также проводить другие исследования функций.
Определение предела функции в точке

Формальное определение предела функции f(x) в точке a гласит: "Предел функции f(x) при x, стремящемся к a, равен L, если для любого положительного числа ε существует положительное число δ такое, что для всех x ≠ a, удовлетворяющих условию |x - a| < δ, выполнено условие |f(x) - L| < ε".
Это определение говорит нам, что если мы хотим найти предел функции в точке a, нам нужно выбрать значение L, такое что для любого положительного числа ε существует такое положительное число δ, что когда x находится в пределах от a-δ до a+δ, значение f(x) находится в пределах от L-ε до L+ε.
Интуитивно можно сказать, что предел функции f(x) в точке a определяет "значение", к которому f(x) стремится при приближении x к a.
Понятие первого предела функции

Представим, что у нас есть функция f(x), заданная на некотором интервале. Мы хотим выяснить, к чему стремится эта функция, когда значение аргумента x приближается к некоторой точке a. Для этого мы можем рассмотреть поведение функции в окрестности точки a и проанализировать, насколько близки значения f(x) к некоторому числу L при достаточно малых значениях |x - a|.
Математический символ для обозначения первого предела функции – это "lim". Обычно запись выглядит следующим образом:
limx→a f(x) = L,
где a – точка, к которой приближается аргумент функции, L – число, к которому стремятся значения функции f(x).
Понимание первого предела функции является фундаментальным для понимания других математических концепций и методов, таких как дифференциальное и интегральное исчисления.
Определение первого предела функции

Определение: Пусть функция f(x) определена на некоторой окрестности точки a, за исключением, возможно, самой точки a. Говорят, что предел функции f(x) при x стремящемся к a равен числу L, и пишут limx→a f(x) = L, если для любого положительного числа ε существует положительное число δ, такое что для всех x, удовлетворяющих условию 0 < |x - a| < δ, выполняется неравенство |f(x) - L| < ε.
В данном определении, a является точкой, к которой стремится аргумент функции, L представляет предел функции, и ε и δ представляют положительные числа, которые используются для описания условия сходимости функции к пределу.
Определение первого предела функции играет важную роль в математическом анализе, так как оно позволяет описывать поведение функции около определенных точек и решать такие вопросы, как непрерывность функции и сходимость рядов. Также, данный концепт имеет широкие применения в физике, экономике и других приложениях, где требуется анализировать изменение переменной по мере ее приближения к определенной точке.
Свойства первого предела функции
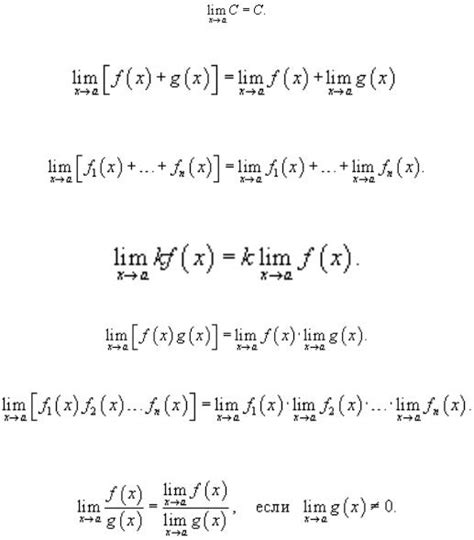
Существует несколько основных свойств первого предела функции:
1. Единственность предела: Для любой функции может быть только один предел в данной точке. Это означает, что функция не может приближаться к разным значениям в одной и той же точке.
2. Условия существования: Предел функции существует только в том случае, если для любого положительного числа можно найти такую окрестность точки, что значения функции в этой окрестности будут лежать в пределах, определенных положительным числом.
3. Линейность предела: Если пределы функций f(x) и g(x) существуют в данной точке, то предел их суммы f(x) + g(x) также существует и равен сумме пределов функций.
4. Значение в пределе: Если предел функции существует в данной точке, то значение функции в этой точке равно пределу.
Знание этих свойств первого предела функции позволяет более глубоко понять и использовать его в математических вычислениях и анализе функций.
Определенность первого предела функции

При изучении пределов функций основное внимание уделяется определению их значений в точках, близких к определенной точке. Определенность первого предела функции связана с поведением функции в окрестности этой точки.
Первый предел функции существует в точке, если существует конечный предел приближения аргумента функции к этой точке. Иными словами, значение функции можно определить и приближая аргумент функции к нужной точке. Если функция ведет себя предсказуемо и показывает аналогичное поведение во всех точках окрестности этой точки, то говорят о определенности первого предела функции в данной точке.
Определенность первого предела функции является одной из важнейших характеристик функции, которая позволяет понять ее поведение и отношение к другим функциям в окрестности данной точки. Знание определенности первого предела функции позволяет проводить множество математических операций с функцией в данной точке и анализировать ее свойства.
Примеры первого предела функции

1. Пример с постоянной функцией:
Рассмотрим функцию f(x) = 2. При приближении аргумента x к любому значению, функция всегда будет равна 2. Таким образом, предел функции f(x) при x стремящемся к любому значению равен 2.
2. Пример с линейной функцией:
Рассмотрим функцию f(x) = 3x + 2. При приближении аргумента x к определенному значению, например, 1, функция будет равна 5. Таким образом, предел функции f(x) при x стремящемся к 1 равен 5.
3. Пример с рациональной функцией:
Рассмотрим функцию f(x) = (x^2 - 1)/(x - 1). При приближении аргумента x к 1, значение функции будет неопределенным, так как в знаменателе будет ноль. Однако, приближаясь к 1 с разных сторон, можно заметить, что значения функции стремятся к 2. Таким образом, предел функции f(x) при x стремящемся к 1 равен 2.
Это лишь несколько примеров первого предела функции. Он может быть определен и вычислен для различных типов функций, и его понимание имеет важное значение для анализа и доказательства различных математических утверждений.