Вершины графа – это одно из самых важных понятий в теории графов. Они являются точками, которые соединяются ребрами, представляющими связи между вершинами. Вершины могут иметь различные свойства и значения, и их анализ и поиск может предоставить много полезной информации о графе.
Поиск вершин графа – это задача, связанная с определением множества вершин, удовлетворяющих определенным условиям. Существует много различных алгоритмов и методов, которые помогают найти вершины графа на основе различных критериев. Некоторые из них используют математические формулы, которые позволяют определить наличие или отсутствие определенных свойств у вершин. В этой статье мы рассмотрим несколько наиболее эффективных и популярных подходов к поиску вершин графа.
Одним из самых простых и распространенных методов поиска вершин графа является метод перебора. Он заключается в том, что все вершины графа последовательно проверяются на соответствие определенным условиям, и, в случае их выполнения, добавляются в множество найденных вершин. Такой подход является достаточно простым, но может быть неэффективным, особенно для больших графов. Более сложные алгоритмы, такие как алгоритмы поиска в глубину или ширину, могут быть более эффективными и позволяют найти вершины графа с меньшими затратами времени и ресурсов.
Вершины графа: обзор и основные понятия

Вершины графа играют важную роль при анализе и обработке данных. При работе с графами можно выделить несколько основных понятий, связанных с вершинами:
- Степень вершины - это число ребер, связанных с данной вершиной. Входная степень – количество входящих ребер, а выходная степень – количество исходящих ребер.
- Смежные вершины – это вершины, которые имеют общие ребра с данной вершиной.
- Петля – это ребро, которое связывает вершину с самой собой.
- Изолированная вершина – это вершина, которая не имеет ребер, связывающих ее с другими вершинами.
Исследование вершин графа позволяет решать различные задачи: нахождение самой удаленной или ближайшей вершины от заданной, определение пути между вершинами, выявление циклов и многое другое. Знание основных понятий, связанных с вершинами графа, помогает понять структуру данных и применить ее для решения конкретной задачи.
Что такое граф и его вершина?
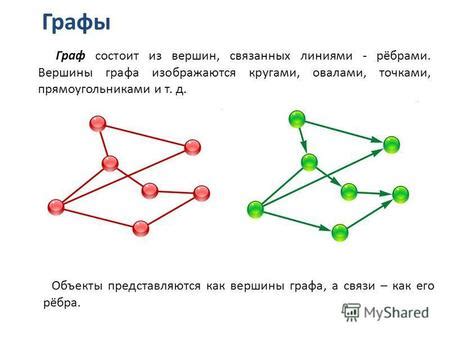
Вершина графа - это один из его элементов, обозначаемый как точка или узел. Каждая вершина может иметь свои характеристики или значения, которые могут быть использованы для представления объектов или явлений из реального мира. Например, в графе, представляющем города и дороги между ними, вершины могут представлять собой отдельные города, а ребра - дороги, соединяющие эти города.
Вершины графа играют ключевую роль, так как через них осуществляется связь между разными элементами графа. Они могут иметь разные связи и отношения с другими вершинами, что позволяет анализировать структуру и взаимодействие элементов внутри графа.
Для работы с графами используются различные алгоритмы и методы, которые позволяют находить и обрабатывать вершины графа. Они могут помочь найти смежные вершины, определить вершину с наибольшей или наименьшей характеристикой, а также найти кратчайший путь между двумя вершинами.
Вершины графа являются фундаментальными элементами этой структуры данных, позволяющими представить и анализировать связи и взаимодействие между различными объектами или явлениями.
Основные характеристики вершин графа

Одной из основных характеристик вершины является ее метка или метаданные. Метка может быть представлена различными значениями, такими как числа, строки или другие объекты, которые несут информацию о вершине. Метки помогают идентифицировать вершины и устанавливать связь с другими элементами графа.
Другой важной характеристикой вершины является ее степень. Степень вершины определяет количество ребер, связанных с данной вершиной. Например, для направленного графа степень вершины будет равна количеству исходящих и входящих ребер. Степень вершины может быть использована для анализа и определения связности графа.
Также, вершины графа могут иметь разные типы связей или отношений с другими вершинами. Например, взвешенный граф может иметь вершины, связанные с помощью весов, которые указывают на значимость или расстояние между ними. Вершины могут иметь также направления связей или отношений, что позволяет представлять различные виды графов, такие как направленные или ненаправленные.
Каждая вершина также может иметь различные атрибуты или свойства, которые помогают дополнительно описать или характеризовать ее. Например, вершина может иметь атрибуты, связанные с ее весом, координатами на плоскости или другими характеристиками, которые могут быть полезны при решении конкретных задач.
Осведомленность об основных характеристиках вершин графа позволяет лучше понимать и использовать эту структуру данных для решения различных задач. Изучение свойств вершин помогает строить алгоритмы, основанные на анализе и обработке данных этой структуры, а также предоставляет полезную информацию для визуализации и восприятия графов.
Поиск вершин графа вручную

Когда требуется найти вершины графа вручную, нужно следовать определенным шагам, чтобы найти нужные точки.
Шаг 1: Взгляните на описание графа и его структуру. Определите, что является вершинами и ребрами графа.
Шаг 2: Изучите граф и найдите возможные вершины. Это могут быть точки соединения между ребрами или точки, в которых сходятся или расходятся несколько ребер.
Шаг 3: Определите, какие из найденных точек являются вершинами. Для этого убедитесь, что вокруг каждой точки есть хотя бы одно ребро.
Шаг 4: Если вершин несколько, пронумеруйте их для удобства дальнейшей работы с графом.
Шаг 5: Проверьте, что каждая вершина соединена ребром с другой вершиной или ребром, ведущим к себе самой. Если это не так, вероятно, вы неправильно представляете граф или упустили какую-то вершину.
Шаг 6: Проверьте правильность номеров вершин и их связей. Сделайте попытку пройти по всем ребрам графа, используя вершины и их номера. Убедитесь, что каждое ребро входит и выходит из правильных вершин.
Найденные вершины являются ключевыми элементами графа и могут использоваться для анализа и работы с ним. Важно точно определить вершины, чтобы избежать неправильных результатов и ошибок в дальнейшей работе с графом.
Методы поиска вершин графа вручную
1. Визуализация графа: Один из способов найти вершины графа вручную - это визуализация графа на листе бумаги или доске. Отмечая узлы и ребра графа, вы можете просмотреть графическое представление и определить вершины.
2. Анализ связей: При анализе графа можно выделить вершины, основываясь на их связях с другими вершинами. Начав с одной вершины и идя по ребрам, вы можете выявить все связанные вершины и считать их вершинами графа.
3. Вычисление степени вершины: Степень вершины графа определяется количеством ребер, смежных с этой вершиной. Вычисление степени каждой вершины может помочь в определении всех вершин графа.
4. Поиск изолированных вершин: Изолированные вершины - это вершины, которые не имеют ребер, связывающих их с другими вершинами. Перебрав все вершины графа, вы можете найти изолированные вершины и считать их вершинами графа.
| Метод | Описание |
|---|---|
| Визуализация графа | Представление графа на листе бумаги или доске |
| Анализ связей | Определение вершин на основе связей с другими вершинами |
| Вычисление степени вершины | Определение вершин на основе количества смежных ребер |
| Поиск изолированных вершин | Поиск вершин, не связанных с другими вершинами |
Использование этих методов может быть полезно для понимания структуры графа и определения его вершин вручную.
Примеры поиска вершин графа вручную
Поиск вершин графа вручную может быть полезным, когда нужно получить быстрый и точный результат. Вот несколько примеров:
| Пример | Описание |
|---|---|
| Пример 1 | Пусть у нас есть граф с вершинами A, B, C, D, E. Мы хотим найти все вершины, с которыми связана вершина A. Переходим к каждой вершине и проверяем, есть ли ребро, соединяющее ее с вершиной A. |
| Пример 2 | Пусть у нас есть взвешенный граф с вершинами A, B, C, D, E. Найдем вершину с наименьшим весом. Для этого переберем все вершины и посчитаем сумму весов исходящих из каждой вершины ребер. В итоге выберем вершину с минимальной суммой. |
| Пример 3 | Пусть у нас есть ориентированный граф с вершинами A, B, C, D, E. Найдем все вершины, к которым можно добраться из вершины A путем прохождения ровно двух ребер. Для этого нужно сначала найти все вершины, с которыми связана вершина A, затем для каждой из этих вершин найти все вершины, с которыми она связана. |
Все эти примеры показывают, что поиск вершин графа вручную может быть достаточно простым и эффективным способом решения задач, связанных с графами.
Поиск вершин графа с использованием алгоритмов
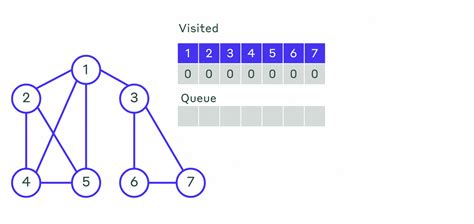
Один из наиболее распространенных алгоритмов для поиска вершин в графе - алгоритм поиска в ширину (BFS). Он использует простую итеративную стратегию, начиная с заданной вершины и проверяя всех ее соседей перед переходом к следующей вершине. Алгоритм BFS обычно используется для нахождения кратчайшего пути или проверки наличия пути между двумя вершинами в невзвешенном графе.
Еще один алгоритм, который эффективно работает при поиске вершин в графе, - это алгоритм поиска в глубину (DFS). Он основан на рекурсивной стратегии, начиная с заданной вершины и исследуя ее соседей в глубину до тех пор, пока не будет найдена вершина с определенными свойствами или пока не будут исследованы все вершины графа. Алгоритм DFS широко используется для проверки связности графа или для нахождения циклов.
Кроме того, существуют и другие алгоритмы поиска вершин в графе, такие как алгоритм Дейкстры для нахождения кратчайших путей во взвешенном графе и алгоритмы поиска потока для нахождения максимального потока в сети.
Выбор конкретного алгоритма для поиска вершин в графе зависит от целей и требований вашего проекта. При выборе алгоритма стоит учитывать сложность времени выполнения, потребление ресурсов и ограничения на граф.
Использование алгоритмов для поиска вершин в графе позволяет эффективно работать с большими объемами данных и решать сложные задачи в различных областях, таких как социальные сети, транспортные системы, генетика и другие.