Математика – это наука, которая базируется на строгой логике и точных вычислениях. Одним из важных понятий, которое изучается в школьной программе, является нахождение площадей различных геометрических фигур. Одной из самых простых фигур является прямоугольник. Его площадь можно вычислить разными способами, и одним из них является методика Петерсона математика.
Методика Петерсона математика – это относительно простой подход, который позволяет легко и быстро найти площадь прямоугольника. Он основывается на учете длины и ширины фигуры, а также на применении алгебраических преобразований.
Для применения методики Петерсона математика необходимо знать длину и ширину прямоугольника. Сначала необходимо измерить длину одной из его сторон и записать полученное значение. Затем измерить ширину прямоугольника и также записать значение.
Площадь прямоугольника по методике Петерсона математика вычисляется по формуле: площадь = длина × ширина. Умножив длину на ширину, получим площадь фигуры. Этот метод позволяет получить точный результат и не требует дополнительных подсчетов.
Методика Петерсона математика для расчета площади прямоугольника
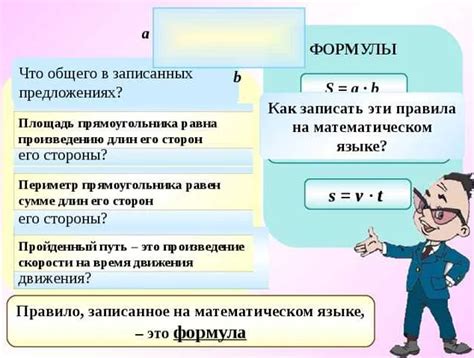
Методика Петерсона математика представляет собой простой и эффективный способ расчета площади прямоугольника. Она основана на принципе разбиения прямоугольника на прямоугольники поменьше и последующем сложении их площадей.
Для применения методики Петерсона математика необходимо знать длину и ширину прямоугольника. Первым шагом необходимо разделить прямоугольник на строки, параллельные его ширине. Каждая строка будет являться прямоугольником со стороной, равной ширине прямоугольника, и высотой, равной длине одной строки.
Далее каждую строку необходимо разделить на столбцы, параллельные его длине. Каждый столбец будет являться прямоугольником со стороной, равной длине прямоугольника, и высотой, равной длине одного столбца.
После разбиения прямоугольника на прямоугольники поменьше, необходимо найти площадь каждого прямоугольника. Площадь прямоугольника можно найти, умножив его длину на ширину.
Наконец, для получения площади исходного прямоугольника необходимо сложить все площади прямоугольников, полученных в результате разбиения, вместе. Полученная сумма будет являться площадью исходного прямоугольника.
Методика Петерсона математика позволяет легко и быстро находить площадь прямоугольника, даже при больших размерах. Она может быть использована как образовательная игра для детей, помогая им освоить основные принципы геометрии и математики.
Преимущества использования методики Петерсона математика
1. Систематический подход Методика Петерсона математика акцентирует внимание на усвоении материала в определенном порядке, от простого к сложному. Это позволяет учащимся получить крепкую основу и последовательно развивать свои навыки. Благодаря систематическому подходу, знания лучше усваиваются и легко применяются в решении сложных математических задач. |
2. Ориентация на понимание Методика Петерсона математика ставит перед собой задачу не просто запоминания формул и правил, а обеспечения понимания математических концепций. Без понимания материала, ученик не сможет успешно применять его в решении сложных задач. Поэтому методика Петерсона акцентирует внимание на объяснении материала и дает возможность учащимся задавать вопросы и уточнять непонятные моменты. |
3. Индивидуальный подход Методика Петерсона математика предоставляет возможность индивидуального обучения каждого ученика в соответствии с его потребностями и уровнем подготовки. Учащиеся могут заниматься в своем темпе, повторять материалы при необходимости и не чувствовать пресса времени. Это позволяет достигать более глубокого понимания математических концепций и уверенности в своих знаниях. |
4. Развитие навыков решения задач Методика Петерсона математика акцентирует внимание не только на усвоении материала, но и на развитии навыков решения задач. В процессе обучения учащиеся решают множество различных задач, начиная с простых и постепенно переходя к более сложным. Это помогает развить логическое мышление, креативность и аналитические навыки, которые являются важными не только в математике, но и в жизни. |
5. Приобщение к практическим примерам Методика Петерсона математика активно использует практические примеры для объяснения материала. Это помогает учащимся увидеть, как может быть применен математический материал в реальных ситуациях. Такой подход делает математику более интересной и понятной, а также помогает ученикам усвоить материал на практике. |
Использование методики Петерсона математика позволяет учащимся достичь более глубокого понимания математических концепций, развить навыки решения задач и приобрести уверенность в своих знаниях.
Шаги для нахождения площади прямоугольника по методике Петерсона математика
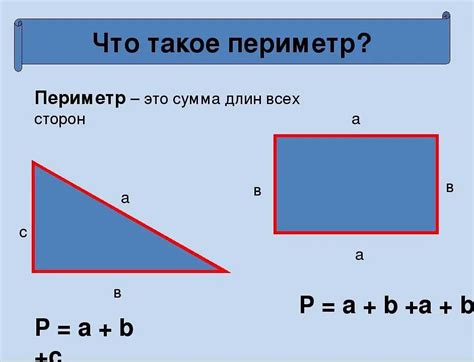
Методика Петерсона математика предоставляет систематический подход к нахождению площади прямоугольника. Для выполнения этой задачи, следуйте следующим шагам:
Шаг 1: Измерьте длину прямоугольника. Пометьте эту величину как "а".
Шаг 2: Измерьте ширину прямоугольника. Пометьте эту величину как "b".
Шаг 3: Перемножьте значения "а" и "b". Полученное число будет площадью прямоугольника.
Пример:
Предположим, что длина прямоугольника равна 5 см, а ширина равна 3 см. Применяя методику Петерсона математика, мы перемножаем эти значения: 5 см * 3 см = 15 см². Таким образом, площадь прямоугольника равна 15 квадратным сантиметрам.
Используя эти шаги, вы можете легко находить площадь прямоугольника по методике Петерсона математика. Запомните, что длина и ширина прямоугольника измеряются в одной и той же единице измерения (например, сантиметры), и площадь будет выражаться в квадратных единицах.