Икс в степени – обычное явление в математике, но часто возникает потребность избавиться от этого двигателя роста. Исходная проблема может быть в различных сферах жизни – от финансового планирования до нахождения способов управления временем. Счастье и успех зависят от наших действий и мыслей, поэтому важно найти эффективные методы, чтобы икс в степени больше не представлял угрозы и не ограничивал наш потенциал.
Правильное мышление – первый шаг к победе над иксом в степени. Часто мы сами себе ставим ограничения, сомневаемся в своих возможностях и боимся неудач. Именно из-за этого икс в степени может расти с каждым днем, пока не станет чем-то непреодолимым. Для того чтобы избавиться от него, необходимо изменить свое мышление и начать верить в себя. Учебные материалы, книги по развитию личности и практика позитивного мышления – вот некоторые способы для начала пути к изменению.
Конкретный план действий – это следующий необходимый шаг в процессе устранения икса в степени. Без плана мы рискуем заблудиться и не достичь поставленных целей. Создание структурированного и реалистичного плана поможет сосредоточиться на конкретных действиях и увидеть прогресс. Разбейте свою цель на маленькие этапы, которые можно достигнуть постепенно. Это позволит вам осознать, что икс в степени вполне реально преодолим.
Проблема: лишние иксы в степени
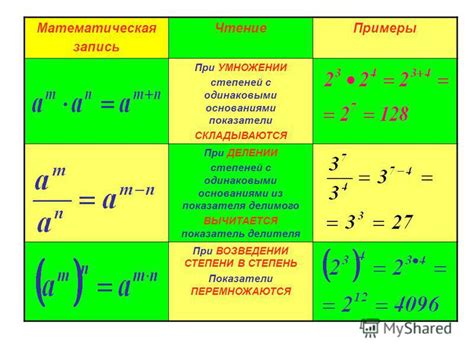
Решение этой проблемы заключается в выполнении ряда математических преобразований, которые позволяют упростить выражения и избавиться от иксов в степенях. Отличные от нуля числа или отличные от единицы степени "x" можно преобразовать с помощью основных свойств степеней.
- Умножение степени "x" на другую степень "x" со сходным основанием: xa * xb = xa + b
- Деление степени "x" на другую степень "x" со сходным основанием: xa / xb = xa - b
- Возведение степени "x" в степень: (xa)b = xa * b
Также можно использовать свойство отрицательной степени:
- Возведение степени "x" в отрицательную степень: x-a = 1 / xa
При решении задач по избавлению от иксов в степенях необходимо помнить о приоритете операций и правилах алгебры, чтобы правильно преобразовывать выражения.
Знание данных методов и правил помогает разрешить проблему с лишними иксами в степенях, делая математические выражения более простыми и понятными.
Определение проблемы

Проблема наличия переменной "икс" в степени может возникнуть в математических и информационных задачах, а также в программировании. Икс в степени может создавать сложности при решении уравнений, нахождении корней, расчете функций и алгоритмах.
В таких случаях, икс в степени может быть неизвестной или неопределенной величиной или переменной, которую необходимо определить. Отсутствие информации о значении "икс" может затруднять точное решение задачи или привести к получению неверных результатов.
Для решения проблемы наличия "икса" в степени необходимо применять специальные методы и техники, такие как аналитическое решение уравнений, итерационные алгоритмы, методы численного анализа, использование программ и компьютерных систем для выполнения вычислений.
Определение проблемы включает в себя анализ постановки задачи, выявление возможных вариантов значений "икса" в степени и обоснование выбора метода или алгоритма для его определения.
Причины возникновения
Математические задачи, содержащие иксы в степени, могут вызывать затруднения в понимании и решении. Это связано с необходимостью умения работать с алгебраическими выражениями и правильно применять правила и свойства алгебры.
Одной из причин возникновения сложностей при работе с иксами в степени является недостаточное знание и понимание основных правил для работы с алгебраическими выражениями. Неправильное применение правил может привести к ошибкам и неправильным результатам.
Ещё одной причиной возникновения затруднений может быть недостаточная подготовка и недостаточное понимание математических концепций. Некоторые учащиеся могут иметь проблемы с переходом от конкретных примеров к абстрактным выражениям и алгебраическим манипуляциям.
Также, неправильное использование алгебраических свойств и правил может стать причиной ошибок и неправильных решений. Например, неправильное раскрытие скобок или неправильное применение свойств степеней может привести к неверному ответу или ошибочному решению задачи.
Наконец, недостаточная тренировка и практика в решении задач может приводить к затруднениям при работе с иксами в степени. Чем больше практики и тренировки, тем лучше развивается навык работы с алгебраическими выражениями и решением подобных задач.
Все эти причины могут быть обусловлены как индивидуальными особенностями учащихся, так и недостаточностью объяснений и практической работы в школе или другом учебном заведении.
Вред, причиняемый иксами в степени

Первое, с чем нужно разобраться, - это основные правила работы с иксами в степенях. Если эти правила неправильно понимать или не усваивать, то затем применять их при решении задач будет чрезвычайно сложно. Необходимо понимать, что возведение "иксов" в степень изменяет их значения и требует применения определенных алгоритмов решения.
Одна из основных проблем, с которой сталкиваются люди при работе с иксами в степенях - это необработанные случаи возведения в степень нормальных чисел или переменных. Неверное использование или непонимание правил приводит к некорректным результатам и ошибкам в вычислениях. Очень важно научиться правильно работать с иксами в степенях, чтобы избежать этих проблем и достичь точных и корректных результатов.
Основные методы избавления от икса в степени
Первый метод – это применение правила степени в степени. Если в степени икса находится другая степень, можно перемножить их и получить новую степень. Например, x в степени 3 возвести в степень 2 можно записать как x в степени 6 (x^3 * x^2 = x^6).
Второй метод – это использование формулы показательной функции. Если икс в степени имеется в знаменателе дроби, можно применить формулу показательной функции, которая гласит: a в степени -n равно одно делить на a в степени n. Например, 1/x в степени 2 можно записать как 1/(x^2).
Третий метод – это применение формулы бинома Ньютона. Если икс в степени находится внутри скобок, можно воспользоваться формулой бинома Ньютона, которая позволяет раскрыть скобки и упростить выражение. Например, (x+1)^2 можно записать как x^2 + 2x + 1.
Четвертый метод – это применение правила умножения степеней с одинаковыми основаниями. Если в выражении присутствуют две степени с одинаковыми основаниями, их можно перемножить и получить новую степень. Например, x в степени 3 умножить на x в степени 4 можно записать как x в степени 7 (x^3 * x^4 = x^7).
Использование этих методов позволяет легко и эффективно избавиться от икса в степени, упростить выражение и решить математическую задачу.
Метод 1: Алгоритм сокращения степеней

Шаги алгоритма сокращения степеней:
- Разложить выражение на множители.
- Использовать свойства степеней для сокращения икса в степени.
- Упростить полученное выражение, если это возможно.
Пример применения метода:
Дано выражение: 3x2 * 2x3
Шаг 1: Разложение на множители:
- Первый множитель: 3x2
- Второй множитель: 2x3
Шаг 2: Сокращение икса в степени:
- Умножение коэффициентов: 3 * 2 = 6
- Сложение показателей степени: x2 + x3 = x5
Полученное упрощенное выражение: 6x5
Метод сокращения степеней позволяет упростить выражения в случае, если они содержат икс в степени с одинаковыми показателями. Он может быть полезен при решении уравнений и работы с алгебраическими выражениями.
Метод 2: Применение формулы Ньютона-Лейбница

Формула Ньютона-Лейбница имеет следующий вид:
∫(f(x) dx) = F(x) + C
где F(x) - первообразная функции f(x), C - произвольная постоянная.
Применение формулы Ньютона-Лейбница позволяет избавиться от икса в степени и преобразовать интеграл в элементарную функцию.
Основной шаг в применении этого метода заключается в нахождении первообразной функции. Первообразная функция f(x) является обратной операцией к дифференцированию функции F(x). Для нахождения первообразной функции можно использовать таблицу интегралов или известные формулы интегрирования.
Применение формулы Ньютона-Лейбница особенно полезно при решении задач на определенный интеграл, так как позволяет сразу найти площадь под графиком функции в заданном интервале. Этот метод широко применяется в математике, физике и других областях, где требуется вычисление площади или накопленной величины.
Примечание: При использовании формулы Ньютона-Лейбница необходимо быть внимательным и учитывать все особенности функции, так как некоторые функции могут иметь специфические интегралы, которые не регулярно выражаются через элементарные функции.
Метод 3: Преобразование икса в корень
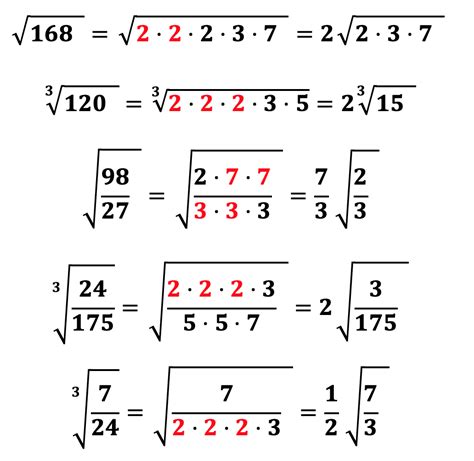
Если в задаче присутствует икс в степени и его необходимо избавиться, то можно воспользоваться методом преобразования икса в корень. Данный метод позволяет упростить выражение и найти его решение.
Шаги для преобразования икса в корень:
- Используя свойство корня, перепишите выражение так, чтобы икс перешел из степени в подкоренное выражение.
- Полученное выражение выглядит следующим образом: корень из (икс).
- Разложите подкоренное выражение на множители, если это возможно.
- Если подкоренное выражение является полным квадратом, то его можно упростить.
- Продолжайте упрощать полученное выражение до тех пор, пока это возможно.
Преобразование икса в корень позволяет существенно упростить выражение, избавиться от икса в степени и найти его решение. Этот метод является одним из эффективных при решении задач, связанных с искомым значением икса.
Метод 4: Замена икса числовым значением

Для начала нужно произвести расчеты, чтобы определить число, на которое следует заменить икс. Для этого можно использовать математические формулы или получить данные из других источников.
После того, как число для замены икса было определено, можно приступить к самой замене. Для этого необходимо использовать соответствующую функцию или алгоритм замены в программном коде.
Одним из простых и популярных способов замены икса числовым значением является использование таблицы. В таблице можно указать все значения, которые нужно заменить, и соответствующие им числовые значения.
| Икс | Числовое значение |
|---|---|
| 1 | 10 |
| 2 | 20 |
| 3 | 30 |
После создания таблицы необходимо просто заменить икс на соответствующее числовое значение из таблицы. Таким образом, икс будет полностью исключен из степени и заменен на числовое значение.
Метод замены икса числовым значением является эффективным и простым способом избавиться от икса в степени. Однако, он подходит только для случаев, когда можно заменить икс на конкретное числовое значение.
Ключевые рекомендации при применении эффективных методов

Для успешного избавления от икса в степени и достижения эффективных результатов следует придерживаться нескольких ключевых рекомендаций.
1. Создайте план действий. Прежде чем приступить к применению эффективных методов, необходимо разработать конкретный план действий. Определите цели, которых вы хотите достичь, и разбейте их на более мелкие подзадачи. Это поможет вам организовать свои усилия и следовать определенному плану.
2. Изучите эффективные методы. Ознакомьтесь с различными методами и подходами, которые помогут вам избавиться от икса в степени. Изучите их особенности, преимущества и недостатки. Выберите те, которые наиболее подходят вам с учетом ваших целей и личных предпочтений.
3. Постепенно внедряйте методы в повседневную жизнь. Внедряйте выбранные методы постепенно и последовательно. Найдите способы интегрировать их в свою повседневную жизнь. Например, если вы решили воспользоваться методом активной визуализации, начните с небольших задач и постепенно увеличивайте их сложность.
4. Будьте последовательны и настойчивы. Чтобы эффективные методы действительно принесли результаты, необходимо быть последовательным и настойчивым. Не сдавайтесь при первой же трудности или неудаче. Продолжайте применять методы и стремиться к своим целям.
5. Не забывайте о самом себе. Важно помнить, что эффективные методы работают в тесной связи с вашим физическим и эмоциональным состоянием. Поэтому не забывайте уделять внимание своему здоровью, отдыху и саморазвитию. Соблюдайте режим дня, занимайтесь спортом, проводите время с семьей и друзьями.
Соблюдение этих ключевых рекомендаций поможет вам избавиться от икса в степени с помощью эффективных методов и достичь желаемых результатов.