Нахождение точек пересечения прямых по уравнениям является одной из фундаментальных задач в алгебре и геометрии. Это ключевой навык, который помогает решать множество задач и применять их на практике. Точки пересечения прямых могут быть полезны при решении задач по построению графиков, вычислению углов, определении взаимного положения фигур и многих других.

Для нахождения точки пересечения двух прямых по их уравнениям требуется решить систему уравнений, состоящую из этих двух уравнений. Существует несколько методов решения этой системы, включая метод подстановки, метод сложения и вычитания, метод определителей и метод Крамера. Каждый из этих методов имеет свои особенности и может быть использован в разных ситуациях.

В этом подробном руководстве мы рассмотрим каждый из этих методов в деталях и предоставим пошаговые инструкции по их применению. Вы узнаете, как записать уравнения прямых в общем виде, как составить систему уравнений, а затем как применить выбранный метод решения для нахождения точки пересечения прямых. Мы также предоставим примеры задач, чтобы продемонстрировать применение этих методов на практике.

Точки пересечения прямых: шаг за шагом

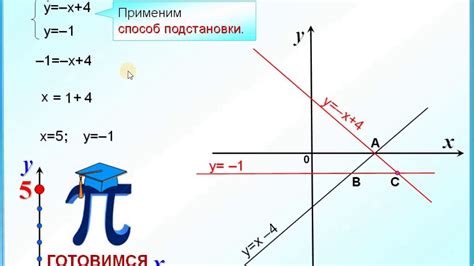
Когда вам требуется найти точки пересечения двух прямых, вы можете использовать уравнения этих прямых. В этом руководстве мы рассмотрим шаги, которые помогут вам найти точки пересечения прямых путем решения системы уравнений.

1. Начните с записи уравнений двух прямых. Уравнение прямой может быть записано в виде y = mx + b, где m - это коэффициент наклона прямой, а b - это свободный член.
2. Поставьте уравнения прямых в систему уравнений, добавив их в пару в виде y₁ = m₁x + b₁ и y₂ = m₂x + b₂.
3. Решите систему уравнений, найдя значения x и y. Можно использовать метод подстановки или метод вычитания.
4. Подставьте найденные значения x и y в одно из исходных уравнений прямых, чтобы найти точку пересечения.
5. Запишите полученную точку пересечения прямых в виде (x, y).

Применяя эти шаги, вы сможете найти точки пересечения прямых по их уравнениям. Не забывайте проверять результаты, подставляя значения в уравнения и убедитесь, что они соответствуют вашим ожиданиям. Удачи в решении!

Методика нахождения точек пересечения прямых по уравнениям

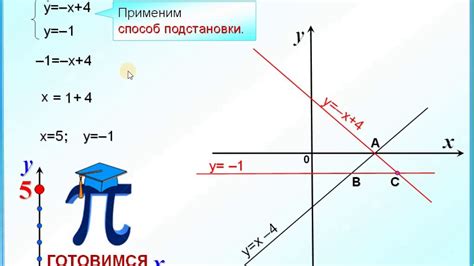
Когда мы имеем два уравнения прямых, заданных в виде y = mx + b, мы можем найти точку их пересечения, используя метод решения систем линейных уравнений.

Для начала, зададим уравнения прямых, например:

y = 2x + 3

y = -3x + 5

Затем объединим эти уравнения в систему:

2x + 3 = -3x + 5

Далее, решим полученное уравнение относительно x, чтобы найти его значение:

2x + 3 + 3x = 5

5x + 3 = 5

5x = 5 - 3

5x = 2

x = 2/5

Теперь, найдя значение x, мы можем подставить его обратно в одно из уравнений прямых для нахождения соответствующего значения y:

y = 2 * (2/5) + 3

y = 4/5 + 3

y = 4/5 + 15/5

y = 19/5

Таким образом, точка пересечения прямых имеет координаты x = 2/5 и y = 19/5.

Получив значение координат точки пересечения, можно заметить, что этот метод позволяет найти ее точные значения и дает возможность визуализировать результат на графике.