Поиск нулевых значений функции на графике является важным аспектом математического анализа. Нулевые значения функции определяются как те значения, при которых функция равна нулю. Они могут иметь большое значение в различных областях знаний, включая физику, экономику и инженерию.
Существует несколько способов найти нулевые значения функции на графике. Один из наиболее распространенных методов – аналитический подход, который основан на алгебраическом решении уравнений. Другой метод – графический подход, который позволяет найти нулевые значения функции путем анализа графика на пересечении с осью абсцисс.
При использовании аналитического подхода необходимо решить уравнение функции, приравняв ее к нулю. Для этого можно использовать различные методы, такие как метод подстановки, метод факторизации, метод дискриминанта и т. д. Эти методы позволяют найти точные значения нулей функции.
Точное определение нулевого значения функции на графике
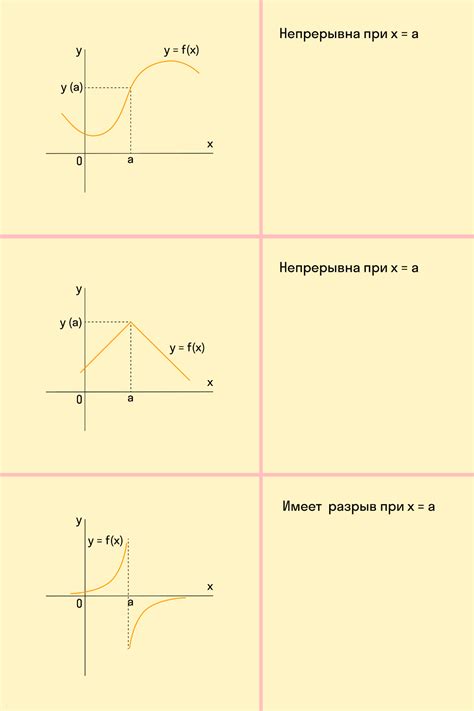
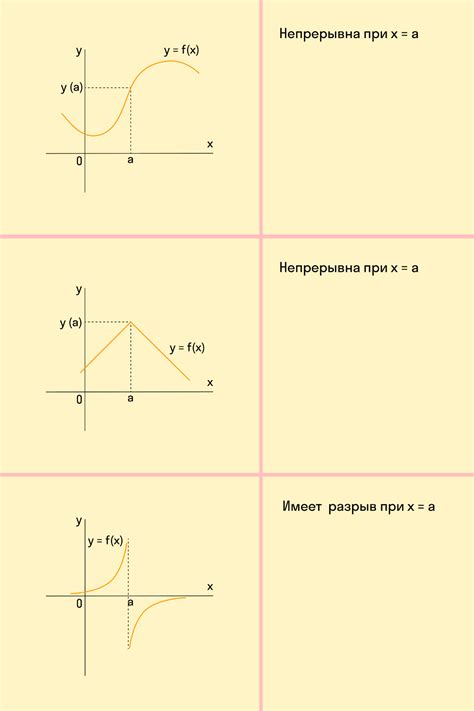
Для определения нулевого значения функции на графике требуется выполнить следующие шаги:
- Найти пересечения с осью абсцисс. Нулевые значения функции на графике соответствуют точкам, где график пересекает ось абсцисс (ось x). Для этого необходимо найти точки графика, в которых значение функции равно нулю.
- Вычислить корни функции. Другой подход заключается в решении уравнения, которое задает функцию. Корни этого уравнения будут нулевыми значениями функции. Для этого нужно приравнять функцию к нулю и решить полученное уравнение.
- Использовать приближенные методы. Если точное определение нулевых значений функции на графике сложно или невозможно, можно использовать численные методы, такие как метод половинного деления или метод Ньютона, для приближенного определения нулевых значений функции.
Важно помнить, что нулевые значения функции могут быть положительными или отрицательными, и их количество может быть разным для разных функций. Для точного определения нулевых значений функции на графике полезно использовать графические методы и математические техники.
Определение нулевых значений функции на графике является важным шагом в изучении математических функций и может помочь в анализе поведения функции в различных точках и интервалах.
Эффективные методы поиска нулевого значения функции на графике

1. Метод бисекции
Метод бисекции основан на принципе деления отрезка пополам и проверки знака функции. Сначала выбирается отрезок, на котором известно, что функция меняет знак. Затем отрезок разделяется пополам, и в каждой части отрезка проверяется знак функции. Если функция меняет знак между двумя точками, то нулевое значение функции находится где-то в этом отрезке. Процесс деления продолжается до достижения заданной точности.
2. Метод Ньютона
Метод Ньютона основан на использовании производной функции для нахождения нулевого значения функции. Идея заключается в том, что касательная к графику функции пересекает ось Х в точке, где значение функции равно нулю. Процесс итеративно повторяется, пока не будет достигнута заданная точность.
3. Метод секущих
Метод секущих является вариацией метода Ньютона и использует линейную аппроксимацию графика функции с помощью секущей. Итерационный процесс повторяется до достижения заданной точности.
4. Метод деления отрезка пополам с использованием итераций
Этот метод сочетает в себе принципы метода бисекции и метода Ньютона. Сначала отрезок разделяется пополам, затем в каждой части отрезка применяется метод Ньютона для нахождения одного нулевого значения функции. Затем процесс деления отрезка и применения метода Ньютона повторяется до достижения заданной точности.
Несмотря на то, что каждый из этих методов имеет свои преимущества и недостатки, их эффективность в нахождении нулевого значения функции на графике обеспечивает возможность выбора оптимального метода в зависимости от задачи и требуемой точности.
Программные инструменты для поиска нулевого значения функции на графике
Существуют различные программные инструменты, которые могут помочь вам найти нулевое значение функции на графике. Эти инструменты обеспечивают эффективный способ решать математические проблемы, особенно связанные с нахождением корней функций.
Один из таких инструментов - компьютерные математические программы, которые позволяют построить график функции и найти его нулевые значения. Программы, такие как MATLAB, Wolfram Mathematica, Python с библиотеками Matplotlib и NumPy, предоставляют мощные средства для математического моделирования и анализа функций. Вы можете визуализировать функцию с помощью графика, а затем использовать функции поиска корней для нахождения мест, где значение функции равно нулю.
Другой способ использования программных инструментов для поиска нулевых значений функции - использование веб-сервисов и интерактивных графических калькуляторов. Они позволяют вам визуально представить функции и найти их нулевые значения, просто вводя уравнение функции или выражение в соответствующие поля. Некоторые из таких сервисов включают в себя Desmos, GeoGebra, Symbolab и Wolfram Alpha.
Важно отметить, что при использовании программных инструментов для поиска нулевых значений функции на графике всегда необходимо быть внимательным и проверять полученные результаты. Также стоит иметь в виду, что эти инструменты могут иметь ограничения по сложности функции или объему данных, поэтому в некоторых случаях может потребоваться более сложный подход или использование специализированного программного обеспечения.