Векторное умножение на число - это одна из фундаментальных операций в линейной алгебре. Понимание этого понятия позволяет решать широкий спектр задач в различных областях, включая математику, физику, программирование и многие другие. В данном руководстве мы рассмотрим, как определить произведение вектора на число практически и познакомимся с основными принципами этой операции.

Произведение вектора на число представляет собой операцию умножения каждой компоненты вектора на заданное число. Это позволяет изменить длину вектора и его направление. Другими словами, произведение вектора на число позволяет увеличить или уменьшить вектор в заданное количество раз и изменить его направление без изменения его свойств.

Для произведения вектора на число необходимо умножить каждую компоненту вектора на это число. Например, если у нас есть вектор a = (a₁, a₂, a₃) и число k, то произведение вектора a на число k записывается как ka и равно (ka₁, ka₂, ka₃). Это означает, что каждая координата вектора умножается на число k.

Применение произведения вектора на число распространено во множестве задач. Например, в физике оно используется для вычисления силы, получаемой при умножении вектора силы на коэффициент. В программировании произведение вектора на число может быть полезно для изменения размера изображения или масштабирования данных. Понимание этой операции пригодится во многих областях, поэтому важно уметь определять произведение вектора на число практически.

Базовые понятия о векторах

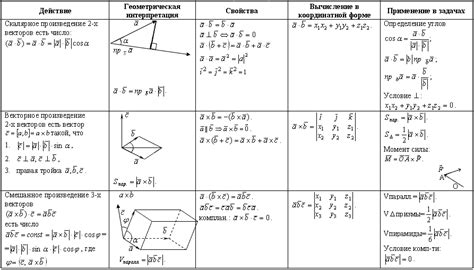
Векторы могут быть представлены в виде упорядоченных пар чисел или матриц. Каждая компонента вектора представляет собой числовое значение, которое указывает на положение в пространстве. Положительное значение компоненты вектора указывает на направление вправо или вверх, а отрицательное значение - на направление влево или вниз.

Сложение и вычитание векторов могут быть выполнены путем складывания или вычитания соответствующих компонент векторов. Умножение вектора на число выполняется путем умножения каждой компоненты вектора на это число.

Для представления векторов в виде упорядоченных пар чисел или матриц может быть использована таблица.

Вектор и его характеристики

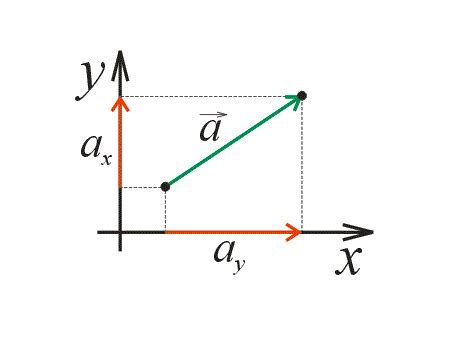
Основные характеристики вектора:

1. Длина - это величина, которая показывает, насколько вектор "протяжен" или "укорочен". Длина вектора может быть определена с использованием математической формулы или геометрически. Часто векторы обозначаются стрелкой над их названием, а длина вектора обозначается модулем, который записывается в виде