Отношение сторон к диагонали - важный аспект в геометрии, который позволяет установить справедливость различных пропорций в фигурах. Этот параметр помогает определить, насколько пропорционален объект или форма, и является неотъемлемой частью изучения геометрии. Знание отношения сторон к диагонали может быть полезно во многих областях, в том числе в строительстве, архитектуре и дизайне.
Что такое отношение сторон к диагонали?
Отношение сторон к диагонали - это соотношение длины сторон фигуры к длине ее диагонали. Обычно это значение представляется в виде десятичной дроби или процента. Например, если у нас есть прямоугольник со сторонами 4 и 6, то его отношение сторон к диагонали составляет 2:3 или 66,67%.
Польза отношения сторон к диагонали
Знание отношения сторон к диагонали имеет множество практических применений. В архитектуре, например, это позволяет определить насколько пропорционален дом или здание. Важно, чтобы стороны и диагонали строительных конструкций были гармонично пропорциональны между собой. Также отношение сторон к диагонали может использоваться в дизайне для создания эстетически приятных комбинаций и композиций.
Что такое отношение сторон к диагонали?
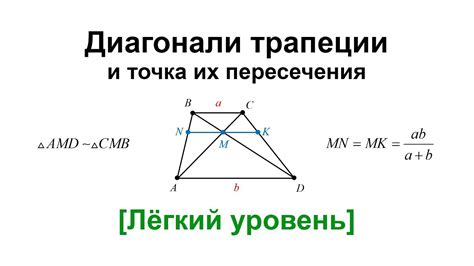
Отношение сторон к диагонали обычно выражается в виде десятичной дроби или в процентах. Для нахождения отношения сторон к диагонали необходимо измерить длины сторон треугольника с помощью линейки или другого инструмента, а также измерить длину диагонали.
Зная отношение сторон к диагонали, можно определить, является ли треугольник прямоугольным, равнобедренным или разносторонним. Например, если отношение сторон к диагонали равно 1 : 2, то это означает, что каждая сторона треугольника в два раза длиннее его диагонали.
| Отношение сторон к диагонали | Тип треугольника |
|---|---|
| 1 : 1 | Равносторонний треугольник |
| 1 : 2 | Равнобедренный треугольник |
| 1 : 3 | Прямоугольный треугольник |
| 1 : 4 | Прямоугольный треугольник |
| 1 : 5 | Прямоугольный треугольник |
| 1 : 6 | Прямоугольный треугольник |
| 1 : 7 или больше | Остроугольный треугольник |
Отношение сторон к диагонали является важным понятием в геометрии и может быть использовано для решения различных задач и построения фигур. Зная отношение сторон к диагонали, можно определить соотношение сторон треугольника, а также его геометрические свойства.
Зачем нужно знать отношение сторон к диагонали?

Одной из практических областей, где знание отношения сторон к диагонали является важным, является строительство и архитектура. Например, при проектировании зданий и сооружений необходимо учесть пропорции и соотношения между сторонами строительных элементов, чтобы обеспечить не только эстетическую привлекательность, но и прочность конструкции.
В инженерных расчетах знание отношения сторон к диагонали используется для определения нагрузок на материалы и структуры. Это позволяет выбирать и применять материалы с учетом их прочностных характеристик и долговечности.
В геометрии отношение сторон к диагонали помогает определить форму и свойства геометрических фигур. Например, знание отношения сторон к диагонали может позволить определить, является ли объект прямоугольником или квадратом, или является ли треугольник равнобедренным.
Иногда знание отношения сторон к диагонали может быть полезно в быту. Например, при выборе телевизора или монитора важно учитывать отношение сторон экрана к диагонали, чтобы получить оптимальное отображение изображения.
Все эти примеры показывают, что знание отношения сторон к диагонали является важным и полезным для решения различных задач в разных областях. Этот параметр помогает определить пропорции и соотношения между сторонами объектов, что имеет большое значение для достижения желаемых результатов и обеспечения эффективного использования ресурсов.
Формула для нахождения отношения сторон к диагонали
| Отношение сторон к диагонали | Формула |
|---|---|
| Отношение a к d | a/d |
| Отношение b к d | b/d |
Применяя эту формулу, можно легко и быстро найти отношение сторон к диагонали в прямоугольнике. Данная информация может быть полезна при решении различных геометрических задач или при создании дизайна и пропорции в различных областях.
Например, если в прямоугольнике длина одной стороны равна 6 сантиметров, а диагональ равна 10 сантиметрам, то отношение стороны к диагонали будет равно 6/10 = 0.6 (или 60%). Таким образом, сторона составляет 60% от длины диагонали.
Как использовать формулу в практике?
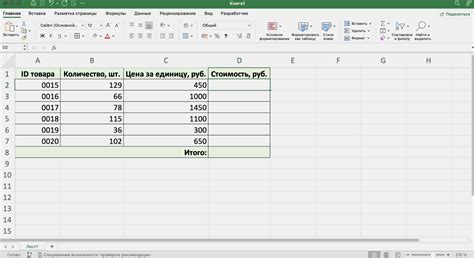
Формула для нахождения отношения сторон к диагонали представляет собой математическое выражение, которое может быть применено на практике при решении различных задач. Эта формула особенно полезна в геометрии, строительстве и дизайне.
Для использования формулы, необходимо знать значения длины сторон и диагонали. Если известны две стороны треугольника и его диагональ, можно использовать формулу для нахождения отношений между этими величинами.
Пример:
Допустим, что у нас есть треугольник ABC, у которого известны стороны AB и AC со значениями 5 и 7 соответственно, и диагональ BD со значением 8. Чтобы найти отношение сторон к диагонали, воспользуемся формулой:
Отношение сторон к диагонали = (Длина стороны 1 + Длина стороны 2) / Длина диагонали
Подставив известные значения, получим:
Отношение сторон к диагонали = (5 + 7) / 8 = 12 / 8 = 1.5
Таким образом, отношение сторон к диагонали треугольника ABC равно 1.5. Это означает, что стороны треугольника в 1.5 раза длиннее его диагонали.
Формула для нахождения отношения сторон к диагонали может быть использована не только для треугольников, но и для других геометрических фигур, таких как прямоугольники, параллелограммы и т.д.
Зная данное отношение, можно рассчитывать длины сторон и диагонали исходя из известных значений, а также находить значения, если известна только одна сторона и отношение сторон к диагонали.
Примеры нахождения отношения сторон к диагонали
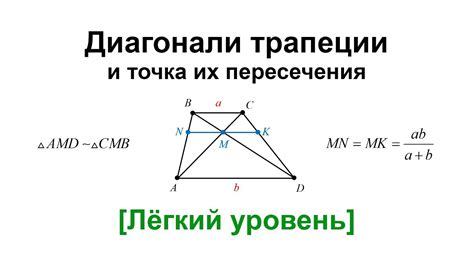
Ниже приведены несколько примеров нахождения отношения сторон к диагонали в различных геометрических фигурах:
Прямоугольник:
Пусть у нас есть прямоугольник со сторонами a и b, а диагональ обозначена как d.
Формула для нахождения отношения сторон к диагонали прямоугольника:
Отношение стороны a к диагонали d: a/d
Отношение стороны b к диагонали d: b/d
Квадрат:
Для квадрата со стороной a и диагональю d отношение стороны к диагонали выглядит следующим образом:
Отношение стороны к диагонали: a/d
Равнобедренный треугольник:
В равнобедренном треугольнике с боковыми сторонами a и диагональю d отношение стороны к диагонали можно выразить так:
Отношение боковой стороны к диагонали: a/d
Равносторонний треугольник:
В равностороннем треугольнике, где все стороны равны a и диагональ обозначена как d, отношение стороны к диагонали такое же:
Отношение стороны к диагонали: a/d
Вышеуказанные формулы помогут вам находить отношение сторон к диагонали в различных геометрических фигурах. Используйте их при решении задач и расчетах в соответствующих областях.
Пример 1: треугольник со сторонами 3 и 4
Для решения задачи по поиску отношения сторон к диагонали в треугольнике, возьмем пример треугольника со сторонами 3 и 4.
По теореме Пифагора, квадрат длины диагонали треугольника равен сумме квадратов длин двух других сторон. В нашем примере, мы имеем треугольник со сторонами 3 и 4, поэтому можем использовать данную формулу для вычисления длины диагонали.
Согласно теореме Пифагора:
диагональ2 = 32 + 42
Подставив значения сторон, получаем:
диагональ2 = 9 + 16 = 25
Для вычисления длины диагонали, извлекаем квадратный корень из полученного значения:
диагональ = √25 = 5
Таким образом, в треугольнике со сторонами 3 и 4, длина диагонали равна 5. Зная эту информацию о треугольнике, можно использовать ее для решения других задач или для проведения геометрических вычислений.
Пример 2: прямоугольник со сторонами 5 и 12
Рассмотрим пример прямоугольника со сторонами 5 и 12. Для нахождения отношения сторон к диагонали нам необходимо использовать теорему Пифагора.
Согласно теореме Пифагора, квадрат длины диагонали прямоугольника равен сумме квадратов длин его сторон. В данном случае, величина диагонали равна:
d² = a² + b²
Где d - длина диагонали, a - длина одной стороны прямоугольника, b - длина другой стороны прямоугольника.
Подставляя значения, получаем:
d² = 5² + 12²
d² = 25 + 144
d² = 169
Извлекая корень полученного значения, получаем длину диагонали:
d = √169 = 13
Таким образом, отношение сторон к диагонали прямоугольника со сторонами 5 и 12 равно 5:12, а длина диагонали равна 13.