Точки разрыва функции двух переменных - это точки, в которых функция не определена или не имеет конечного значения. Они могут являться важным фактором при анализе и построении графиков функций. Найти эти точки может быть сложной задачей, но существуют определенные методы и подходы, которые помогут вам в этом процессе.
Одним из первых методов, которые стоит попробовать, является анализ функции на наличие разрывов в ее определении. Разрывы могут возникать, когда знаменатель функции обращается в ноль, или когда функция содержит квадратный корень из отрицательного числа. Важно помнить, что для определения точек разрыва функции нужно рассматривать и числитель, и знаменатель функции.
Кроме того, есть еще несколько методов, которые могут помочь в поиске точек разрыва функции двух переменных. Один из них - это построение графика функции. График может помочь в визуализации точек разрыва, особенно если функция представлена в виде сложной формулы с несколькими переменными. Другим методом является анализ функции на предмет симметрии. Если функция является нечетной или четной, то это может указывать на наличие точек разрыва в нуле.
Методы поиска точек разрыва функции двух переменных

Точки разрыва функции двух переменных имеют особое значение в анализе многомерных функций. Они представляют собой места, где функция может быть непрерывной либо недифференцируемой.
Существует несколько методов для поиска точек разрыва функции двух переменных:
- Аналитический подход: данный метод основан на анализе выражения функции и вычислении ее производных. Разрыв функции может возникнуть, если производная не существует в определенной точке или является бесконечной. Для определения точек разрыва необходимо найти такие значения переменных, при которых производные функции не существуют или являются бесконечными.
- Графический подход: в этом методе функция представляется в виде графика на координатной плоскости. Разрыв функции может быть виден непосредственно на графике в виде скачка или разрыва кривой. Необходимо внимательно изучить график функции и найти такие точки, где возникают скачки или разрывы.
- Численные методы: эти методы основаны на численном аппроксимации значений функции и производных. Они позволяют искать точки разрыва приближенно, используя численные методы дифференцирования и интегрирования. Некоторые из таких методов включают метод конечных разностей, метод Ньютона и метод Монте-Карло.
Важно отметить, что нахождение точек разрыва функции двух переменных требует аккуратного и тщательного анализа функции, ее производных и графика. Наличие точек разрыва может указывать на особенности функции и иметь важное значение в решении различных задач.
Анализ графика функции
Для анализа графика функции необходимо провести следующие шаги:
- Построить график функции с помощью математического программного обеспечения или с использованием графического калькулятора.
- Изучить характеристики графика, такие как экстремумы, точки перегиба, асимптоты, пересечение осей координат.
- Отследить наличие разрывов графика, таких как точки разрыва первого рода (удаление, сложение, изменение знака), точки разрыва второго рода (вертикальные, скачкообразные, разрывы функции).
- Используя полученные данные, определить типы разрывов функции и их местоположение.
Анализ графика функции позволяет получить визуальное представление о ее поведении и определить возможные точки разрыва. Это полезный инструмент при изучении функций двух переменных и может помочь в проведении дальнейшего математического анализа.
| Тип разрыва | Описание | Пример |
|---|---|---|
| Точка разрыва первого рода | Функция имеет разные значения слева и справа от точки разрыва | f(x) = 1/x |
| Точка разрыва второго рода | Функция не имеет определенного значения в точке разрыва | f(x) = 1/x^2 |
Проверка границ области определения
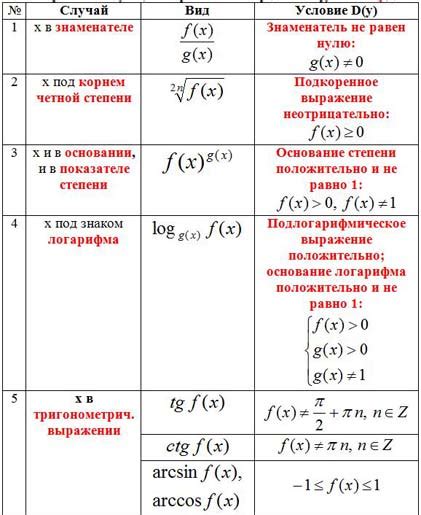
При поиске точек разрыва функции двух переменных важно внимательно проанализировать границы области определения функции. Из-за наличия различных ограничений на значения переменных могут возникать особые ситуации, в которых функция может иметь различные типы разрывов.
Для начала необходимо определить допустимые значения переменных функции. Если область определения функции является ограниченной, то необходимо проверить границы данной области. Это можно сделать путем проверки значений функции на границах области определения.
Если значения функции на границе области определения стремятся к бесконечности или имеют различные предельные значения, то это может указывать на разрыв функции. Необходимо проанализировать поведение функции вблизи границ и установить его непрерывность или разрыв.
Кроме того, важно учесть наличие точек, в которых функция может быть неопределена. Например, функции, содержащие знаки деления или квадратного корня, могут иметь точки разрыва в случае, когда знаменатель равен нулю или аргумент под корнем отрицательный.
Поиск точек разрыва внутри области определения
Для поиска точек разрыва внутри области определения функции двух переменных необходимо проанализировать её поведение в каждом из её аргументов и исследовать возможные особые случаи.
Первый шаг - определить область определения функции. Для этого нужно исследовать знаменатель функции, так как разрыв может возникнуть только в точках, где знаменатель обращается в ноль. Затем необходимо найти все такие точки и проверить их наличие в области определения функции.
После того, как область определения функции определена, можно приступить к анализу её поведения в каждом из аргументов. Для этого следует исследовать пределы функции вблизи точек разрыва и определить, как функция себя ведет при приближении к этим точкам справа и слева. Если пределы различаются, то в точке разрыва имеется разрыв I рода. Если пределы существуют, но не совпадают, то имеется разрыв II рода. Если пределы не существуют, то точка разрыва называется разрывом III рода.
Возможные особые случаи, которые могут возникнуть при поиске точек разрыва, включают:
- Наличие асимптот - горизонтальных, вертикальных или наклонных. При наличии асимптот нужно определить, как они влияют на поведение функции вблизи точек разрыва.
- Существование лимитов и пределов. Важно учесть, что некоторые разрывы могут возникнуть из-за того, что лимит или предел не существуют.
- Свойства функции в области определения. Иногда функции могут обладать определенными свойствами внутри области определения, которые также влияют на наличие разрывов.
В результате анализа всех указанных выше факторов можно найти и классифицировать все точки разрыва функции двух переменных внутри её области определения.
Использование производных для поиска разрывов

Однако, если в точке производная функции не существует, это может быть признаком разрыва функции. Существуют два основных типа разрывов: точечные разрывы и разрывы второго рода.
Точечные разрывы могут быть классифицированы в точки разрыва первого рода и устранимые разрывы. В точках разрыва первого рода, левая и правая производные в данной точке существуют, но имеют разные значения. Устранимые разрывы характеризуются тем, что функция имеет разрыв в данной точке, но его можно устранить, добавив или удалив точку.
Разрывы второго рода характеризуются тем, что в данной точке производная функции не существует ни слева, ни справа. Такие разрывы могут быть разные: разрывы руки, логарифмические разрывы, разрывы второго порядка и т.д.
Для определения разрывов функции двух переменных можно воспользоваться правилами дифференцирования. Например, если производная по одной из переменных расходится при приближении к заданной точке, это может свидетельствовать о существовании разрыва в данной точке.
Использование производных для поиска разрывов функции двух переменных является эффективным инструментом для анализа поведения функции и определения ее особенностей в заданных точках. С помощью этого метода можно выявить различные типы разрывов и оценить их характеристики.