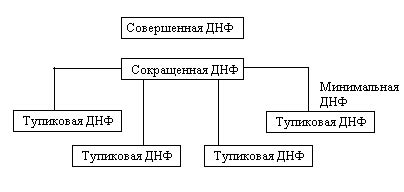
Тупиковая ДНФ (дизъюнктивная нормальная форма) - это выражение логики, которое состоит из конъюнкций литералов, причем каждый литерал может быть отрицанием переменной или самой переменной. Тупиковая ДНФ позволяет представить логическую функцию в виде совокупности множеств ее значений, которые являются истинными. Однако, часто бывает необходимость проверки, является ли данная ДНФ тупиковой. И вот здесь на помощь приходит эффективный алгоритм проверки.
Основной идеей эффективного алгоритма проверки тупиковой ДНФ является то, что каждая дизъюнкция - это неотрицаемое множество переменных, которые являются литералами. Если две дизъюнкции имеют общее множество литералов, то можно заметить, что одна дизъюнкция является подмножеством другой. Используя эту идею, можно эффективно проверить, является ли данная ДНФ тупиковой.
Возможный алгоритм проверки тупиковой ДНФ состоит из нескольких шагов. Первым шагом является построение списка дизъюнкций, представленных в виде множеств литералов. Затем, мы проверяем, есть ли две дизъюнкции с общим множеством литералов. Если такая пара дизъюнкций найдена, то одна дизъюнкция является подмножеством другой, а значит, ДНФ является тупиковой. Если таких пар не найдено, то ДНФ не является тупиковой.
Тупиковая ДНФ: что это?

Тупиковая ДНФ имеет важное значение в области автоматической проверки и анализа программного обеспечения. Она позволяет компактно и эффективно выразить набор условий, при которых выполняется определенное действие или срабатывает определенное событие.
Однако, в некоторых случаях, тупиковая ДНФ может быть неэффективной или содержать ненужные условия, которые не влияют на результат. Такие условия называются "тупиковыми". Они могут возникать при ручном или автоматическом построении ДНФ.
Для проверки наличия тупиковых условий в ДНФ существуют различные алгоритмы и методы. Они позволяют определить, является ли ДНФ тупиковой, и, если является, найти и удалить тупиковые условия. Это позволяет упростить логическую схему, сократить количество условий и улучшить производительность проверки или анализа программного обеспечения.
| Операция | Описание | Пример |
|---|---|---|
| ИЛИ | Логическое ИЛИ, результат будет истинным, если хотя бы один из аргументов истинный. | A ИЛИ B: истина, если A истина или B истина. |
| Отрицание | Логическое отрицание, инвертирует значение аргумента. | !A: истина, если A ложна. |
ДНФ: основы и применение

ДНФ состоит из набора элементарных дизъюнкций (сумм) логических переменных, которые объединены операцией "ИЛИ". Каждая элементарная дизъюнкция представляет собой конъюнкцию (произведение) литералов (переменных или их отрицаний), соединенных операцией "И".
Проверка тупиковости ДНФ - важный аспект ее использования. Тупиковая ДНФ представляет такую булеву функцию, которая равна нулю на всех возможных наборах значений переменных. Проверка тупиковости позволяет определить, существуют ли наборы переменных, на которых функция может равняться единице, что особенно полезно при анализе и оптимизации каскадных логических схем и систем.
Для эффективной проверки тупиковости ДНФ можно использовать различные алгоритмы и методы, такие как методы аналитического или алгебраического решения систем уравнений, процедуры отделения и сокращения дизъюнкций и другие. Одним из практических подходов является проверка тупиковости ДНФ путем перебора всех возможных наборов переменных и проверки значений функции на этих наборах.
Успешное применение ДНФ в различных областях, таких как программирование, математика, электроника и теория систем, подтверждает ее ценность и актуальность в современной науке и практике.
Тупиковая ДНФ: понятие и значение

Тупиковая ДНФ (дизъюнктивная нормальная форма) представляет собой одну из формальных логических систем, используемую в вычислительной технике, математике и информатике. ДНФ применяется для описания логических схем, условных выражений и булевых функций.
Тупиковая ДНФ – это особая разновидность ДНФ, в которой не существует других максимальных термов, покрывающих данную функцию. Другими словами, тупиковая ДНФ представляет собой самую простую форму записи булевой функции с неповторяющимися термами, не поддающуюся дальнейшей минимизации.
Понимание и использование тупиковой ДНФ имеет значительную важность в области доказательства корректности программного кода, конструирования схем электронных узлов и создания оптимизированных алгоритмов. Тупиковая ДНФ позволяет упростить и оптимизировать вычисление сложных булевых функций, а также вычисление логических значений, необходимых для принятия решений внутри программного кода.
Тупиковая ДНФ облегчает понимание и анализ логических условий и выражений, что способствует повышению надежности программного обеспечения и эффективности вычислений.
Методы проверки тупиковой ДНФ
Существует несколько методов эффективной проверки тупиковой ДНФ:
- Метод Квайна: данный метод предлагает последовательно применять операции смешения и подъема. Сначала применяется операция смешения, при которой проверяется, есть ли два терма, в одном из которых положение j-го литерала отличается от терма в другом, и при этом оба терма покрывают строки с 1 в j-й позиции. Если такие термы находятся, то они смешиваются и образуют новый терм. Затем осуществляется операция подъема, при которой проверяется, есть ли два терма, из которых один является подтермом другого на всех позициях, кроме одной. Если такие термы находятся, то подтерм удаляется.
- Метод Квайна-Мак-Клиски: данный метод является модификацией метода Квайна. Он заключается в применении операций смешения и подъема до тех пор, пока больше ни одна из этих операций не может быть выполнена. Этот метод позволяет более быстро проверить, является ли ДНФ тупиковой.
- Метод многократного подъема: данный метод заключается в применении операции подъема до тех пор, пока возможно поднять хотя бы один терм. Если после применения операции подъема все термы, кроме "1" (единицы), удаляются, то ДНФ является тупиковой.
Выбор метода для проверки тупиковой ДНФ зависит от её размера и структуры. В некоторых случаях могут быть эффективны и другие методы, разработанные для решения конкретных задач.
Важно выбирать подходящий метод для каждой конкретной задачи, чтобы достичь наиболее эффективного результата и сократить время выполнения проверки.
Метод отсечений
Процесс проверки тупиковой ДНФ с использованием метода отсечений состоит из следующих шагов:
- Инициализация: создаем пустое множество, которое будет хранить конъюнкции, которые нужно проверить.
- Добавление конъюнкций: добавляем все конъюнкции из тупиковой ДНФ в созданное множество конъюнкций.
- Отсечение: для каждой конъюнкции в множестве конъюнкций применяем логические правила. Если результат применения правил равен ложь, то конъюнкция является ненужной и удаляем ее из множества конъюнкций.
- Повторение: повторяем шаг 3 до тех пор, пока множество конъюнкций не останется пустым или не будет достигнут предел итераций.
- Выход: если на выходе получаем пустое множество конъюнкций, то тупиковая ДНФ является проверенной и не содержит ненужных конъюнкций.
Метод отсечений позволяет уменьшить количество конъюнкций, которые нужно проверить, и ускорить процесс проверки тупиковой ДНФ. Однако он не гарантирует полное исключение всех ненужных конъюнкций, поэтому в некоторых случаях может потребоваться дополнительная проверка.
Методы базисных векторов

В начале проверки тупиковой ДНФ, нам необходимо сгенерировать все возможные базисные векторы для заданного количества переменных. Базисный вектор - это комбинация значений переменных, при которой ДНФ обращается в истину. Для генерации базисных векторов мы могли бы использовать бинарный счетчик, в котором каждый бит счетчика представляет одну переменную.
После генерации всех базисных векторов, мы можем применить их ко всем дизъюнктам ДНФ и проверить, будут ли все дизъюнкты обращаться в ложь при заданной комбинации переменных. Если хотя бы один дизъюнкт обращается в истину для всех базисных векторов, то ДНФ является тупиковой. Если же все дизъюнкты обращаются в ложь для всех базисных векторов, то ДНФ не является тупиковой.
Преимущество метода базисных векторов заключается в его эффективности. Вместо проверки всех возможных комбинаций переменных, таких как в методе полного перебора, мы проверяем только базисные векторы. Это позволяет значительно ускорить процесс проверки и экономит вычислительные ресурсы.
Таким образом, применение метода базисных векторов является эффективным подходом для проверки тупиковой ДНФ. Он позволяет быстро определить, является ли ДНФ тупиковой, и применяется в различных областях, таких как формальная верификация и оптимизация логических функций.
Метод редукции

Для применения метода редукции необходимо выполнить следующие шаги:
- Рассмотреть все импликанты ДНФ и найти такие пары импликантов, у которых одинаковые значения на фиксированных переменных и разные значения на оставшихся переменных.
- Выбрать одну из найденных пар и объединить их, фиксируя значение переменных на которых они совпадают.
- Рекурсивно повторить шаги 1 и 2 с полученной после объединения пары импликантов ДНФ.
- Продолжать процесс, пока не будет достигнута тупиковая ДНФ, состоящая из одной импликанты.
Таким образом, метод редукции позволяет сократить количество переменных, по которым нужно проводить проверку, и тем самым упрощает процесс верификации тупиковой ДНФ.
Метод редукции основан на принципе, что если импликанты ДНФ совпадают на некоторых переменных, то их значения на оставшихся переменных могут быть любыми.
Примечание: Метод редукции не всегда приводит к полному решению задачи проверки тупиковой ДНФ, но позволяет существенно сократить количество возможных комбинаций переменных для проверки.