Корень числа - это такая математическая операция, которая позволяет найти число, при возведении которого в заданную степень получается данное число. Возведение в корень - это обратная операция к возведению в степень. Когда мы говорим "корень двух" или "корень из числа", мы имеем в виду найти такое число, которое, возведенное в квадрат, равнялось бы данному числу. Вычисление квадратного корня является одной из базовых операций в математике и имеет множество способов и формул.
Первый и самый простой способ вычисления корня числа - это использование таблицы квадратных корней. В такой таблице вы можете найти квадратные корни для предопределенного набора чисел. Найдя число, для которого в таблице есть квадратный корень, вы сможете определить его значение без калькулятора. Но таблица имеет ограниченный набор чисел, и вычисление корня для числа, которого нет в таблице, потребует дополнительных усилий.
Если вам понадобилось вычислить корень для числа, не представленного в таблице, существуют различные методы и формулы для выполнения этой операции. Например, метод деления отрезков позволяет приближенно найти корень числа, разбивая интервалы на меньшие отрезки и проверяя, где находится искомый корень. Еще одним способом является метод итераций, при котором на каждом шаге вычисления использованное число заменяется на приближенное значение, пока не будет достигнута необходимая точность.
Как вычислить корень числа?

- Методы приближенного вычисления: приближенные значения корня можно получить с помощью методов, таких как метод деления отрезка пополам, метод касательных или метод Ньютона. Эти методы основываются на итерациях и позволяют приближенно вычислить корень числа.
- Использование таблицы корней: для некоторого ограниченного набора значений можно использовать таблицу корней, чтобы быстро найти приближенное значение корня числа. Например, можно составить таблицу квадратных корней и использовать ее для вычисления корней чисел.
- Использование перебора: для небольших чисел можно использовать метод перебора, который заключается в последовательном проверке всех чисел от 1 до исходного числа. Найденное число, при возведении в квадрат, должно быть близким к исходному числу.
Разные методы вычисления корня числа могут быть эффективны в разных ситуациях. Выбор метода зависит от точности, скорости вычисления и доступности инструментов для вычисления.
Метод нахождения корня путем возведения в степень

Для того чтобы вычислить корень числа, можно возвести это число в некоторую степень и получившееся число приближенно равное корню. Затем можно последовательно улучшать приближение, изменяя значение степени.
Применение этого метода довольно просто. Сначала необходимо выбрать начальное приближение для корня. Затем нужно возвести выбранное число в некоторую степень. Если полученное значение отличается от исходного числа не более, чем на заданную погрешность, то выбранное число является приближенным значением корня. Если полученное значение больше исходного числа, то степень нужно уменьшить. Если полученное значение меньше исходного числа, то степень нужно увеличить. После каждого увеличения или уменьшения степени, необходимо снова возвести число в данную степень и сравнить результат с исходным числом. Этот процесс необходимо повторять до достижения необходимой точности.
Приведем пример. Пусть нам нужно вычислить корень из числа 27 с погрешностью не более 0.001. Начальное приближение для корня в этом случае может быть 3. Возводим число 3 в степень 3: 33 = 27. Полученное значение равно исходному числу, поэтому 3 является приближенным значением корня. Поскольку у нас есть корень, равный 3, погрешность не превышает 0.001, и мы можем остановиться.
Следует отметить, что метод нахождения корня путем возведения в степень является итерационным, поэтому может потребоваться несколько итераций, чтобы достичь необходимой точности. Однако он может быть полезным для ручного вычисления корня числа без использования калькулятора и легко реализуется с помощью простых алгоритмов.
Простой алгоритм вычисления корня числа
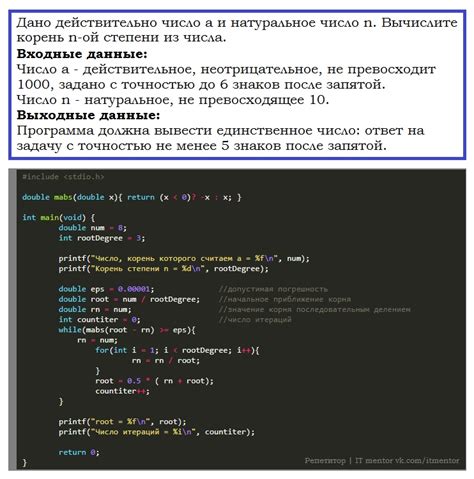
Алгоритм начинается с предположения о значении корня итерации, которое может быть выбрано произвольно. Затем происходит последовательное уточнение значения корня с помощью простых математических операций.
| Шаг | Вычисление значения |
|---|---|
| 1 | Предположить значение корня, например, 1 |
| 2 | Вычислить новое значение корня с помощью формулы: новое_значение = (старое_значение + (число / старое_значение)) / 2 |
| 3 | Повторить шаг 2 определенное количество раз или до достижения необходимой точности |
Последовательное повторение шагов 2 и 3 позволяет уточнять значение корня до достижения необходимой точности. Чем больше итераций произведено, тем более точным будет значение корня.
Этот простой алгоритм вычисления корня числа может быть реализован в различных программах и языках программирования, и он предоставляет несложный способ получения приближенного значения корня без использования калькулятора.
Использование метода Ньютона для нахождения корня
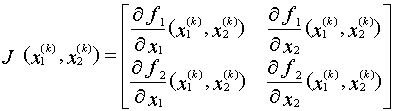
Применение метода Ньютона для нахождения корня числа происходит следующим образом:
- Выбирается начальное значение x0, которое будет использоваться в качестве первого приближения корня.
- Вычисляется значение функции f(x) в точке x0.
- Находится значение производной функции f'(x) в точке x0.
- Вычисляется следующее приближение корня по формуле: x1 = x0 - f(x0) / f'(x0).
- Шаги 2-4 повторяются до достижения заданной точности или сходимости.
Метод Ньютона сходится быстро и обычно требует меньшего количества итераций, чем другие методы приближенного нахождения корней. Однако он требует знания функции и ее производной, что может быть нетривиальной задачей в некоторых случаях.
Если правильно применить метод Ньютона, можно достичь точных результатов и вычислить корень числа без использования калькулятора. Однако стоит учитывать, что неправильное выбор начального значения x0 или слишком большое количество итераций может привести к некорректным результатам или зацикливанию, поэтому необходимо быть осторожным при использовании данного метода.
Итерационный способ расчета корня

Алгоритм итерационного способа состоит из следующих шагов:
- Выбор начального приближения корня.
- Вычисление следующего приближения корня на основе предыдущего приближения исходного числа.
- Повторение шага 2 до достижения достаточной точности вычислений.
Данный способ основан на использовании итерационной формулы:
xn+1 = (xn + a/xn)/2,
где xn - текущее значение приближения, xn+1 - следующее значение приближения, a - исходное число, для которого осуществляется расчет корня. Первое значение приближения (x0) можно выбрать произвольно.
Итерационный способ расчета корня позволяет достаточно точно приблизиться к истинному значению корня числа. Чем больше количество итераций, тем точнее будет полученный результат. Однако нужно учитывать, что вычисления могут потребовать большого количества шагов для достижения необходимой точности.
Алгоритм вычисления корня кубического числа

В математике кубическим корнем числа называется число, которое при возведении в куб равно исходному числу. Кубический корень может быть вычислен без использования калькулятора или специальных формул с помощью простого алгоритма.
Для вычисления кубического корня числа можно использовать метод подбора. Процесс заключается в итеративном уточнении значения корня.
В начале алгоритма выбирается первое приближение к корню. Затем это приближение используется для получения нового значения корня. Этот шаг повторяется до достижения требуемой точности.
Алгоритм выглядит следующим образом:
- Выберите начальное приближение к корню.
- Используйте выбранное приближение для вычисления нового значения корня.
- Повторяйте шаг 2 до тех пор, пока не достигнете требуемой точности.
Для каждого шага вычисления нового значения корня используется формула:
xn+1 = (2 * xn + a / xn2) / 3
где xn+1 – новое приближение к корню, xn – предыдущее приближение к корню, а – число, для которого вычисляется кубический корень.
Этот алгоритм позволяет вычислить приближенное значение кубического корня числа без использования специальных формул или калькулятора.
Метод деления отрезка пополам
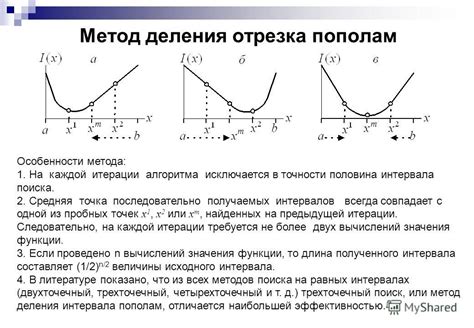
Для начала выбирается интервал [a, b], в котором находится искомый корень. Затем производится деление этого интервала пополам на отрезки [a, c] и [c, b], где c = (a + b) / 2.
Затем определяется значение функции f(c). Если f(c) равно нулю или достаточно близко к нулю, то c является корнем, в противном случае выбирается интервал, границы которого находятся с разных сторон от корня. Этот процесс повторяется до достижения желаемой точности или максимального количества итераций.
Метод деления отрезка пополам обладает простой реализацией и обеспечивает сходимость к корню. Однако, он может быть неэффективным, если искомый корень находится далеко от начального интервала.
Использование математических таблиц для нахождения корня

Для использования математической таблицы для нахождения корня необходимо следующее:
- Определить значение числа, из которого нужно извлечь корень.
- Оценить близкое значение корня путем примерного позиционирования числа на таблице.
- Искать число в таблице, ближайшее к оценке значения корня.
- Получить более точное значение корня из таблицы или применить формулы для интерполяции значения.
Использование математических таблиц для нахождения корня имеет свои преимущества и недостатки. С одной стороны, это относительно простой способ получить приближенное значение корня, особенно если доступ к инструментам вычисления ограничен. Однако, он требует умения пользоваться таблицей и может быть нестабильным для вычислений с высокой точностью.
Важно отметить, что использование математических таблиц для нахождения корня требует знания и понимания математических принципов. Правильная интерпретация и применение значений в таблице являются ключевыми для получения более точных результатов.
В любом случае, использование математической таблицы для нахождения корня может быть полезным инструментом, если нет доступа к калькулятору или другим средствам вычисления, и если точность результата не является критически важной.
Алгоритм вычисления корня числа с использованием бинарного поиска
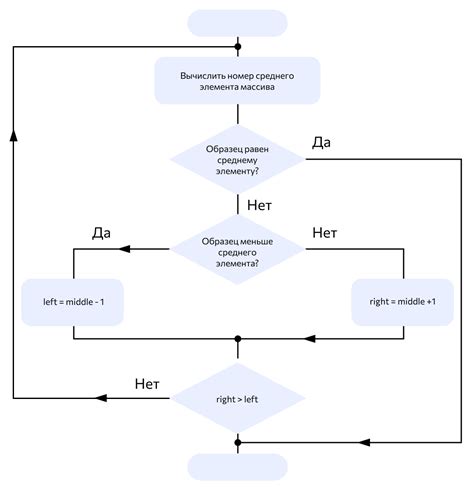
Для начала необходимо определить границы корня: нижнюю (левую) и верхнюю (правую). Их можно выбрать таким образом, чтобы искомое число находилось между ними. Например, если мы ищем корень числа n, то нижняя граница может быть равна 0, а верхняя – самому числу n.
Далее проводится итеративный процесс бинарного поиска, который включает следующие шаги:
- Находим среднее значение между нижней и верхней границей: mid = (low + high) / 2.
- Сравниваем полученное среднее значение с числом, корень которого мы ищем.
- Если среднее значение меньше числа, корень которого мы ищем, то новой нижней границей становится среднее значение, а верхняя граница остается прежней. В противном случае, новой верхней границей становится среднее значение, а нижняя граница остается прежней.
- Процесс повторяется до тех пор, пока не будет достигнута нужная точность или найден искомый корень числа. Нужную точность можно определить на основе требуемого количества знаков после запятой или заданной разницы между квадратом полученного значения и искомым числом.
Таким образом, бинарный поиск позволяет эффективно приближаться к корню числа, путем деления отрезка пополам на каждом шаге и выбора подотрезка, в котором находится искомый корень.
Данный алгоритм может быть полезен в различных сферах, таких как математика, программирование и инженерия. Он позволяет найти корень числа без необходимости использования калькулятора, что упрощает и ускоряет расчеты.
Приближенные методы нахождения корня числа

В некоторых случаях точное вычисление квадратного корня из числа может быть достаточно сложной задачей. Однако существуют приближенные методы, которые позволяют получить достаточно точный результат.
Один из таких методов - это метод Ньютона. Он основан на итерационном процессе вычисления корня числа.
Метод Ньютона заключается в следующем:
- Выбирается начальное приближение корня.
- Вычисляется следующее приближение корня путем деления числа на текущее приближение и получения среднего значения между текущим приближением и результатом деления.
- Шаг 2 повторяется до достижения требуемой точности.
Также существуют другие приближенные методы, такие как метод деления отрезка пополам и метод приближения постепенным увеличением границы интервала.
При использовании этих методов следует помнить, что точность результата зависит от выбора начального приближения и числа итераций. Чем больше итераций и более близкое начальное приближение, тем точнее будет результат. Однако слишком большое количество итераций может привести к потере точности из-за ошибок округления.
Применение калькуляторов для нахождения корня

Существует множество способов вычислить корень числа без использования калькулятора, однако в некоторых случаях возникает необходимость использовать электронные устройства для решения этой задачи. Калькуляторы облегчают вычисления и позволяют быстро получить точный результат.
Современные научные калькуляторы часто имеют встроенную функцию вычисления корня. Для этого необходимо ввести значение числа и указать степень корня. Калькулятор автоматически вычислит корень и выдаст результат с заданной точностью.
Если у вас нет научного калькулятора, можно воспользоваться обычным калькулятором с возможностью вычисления корня. Для этого необходимо сделать следующие действия:
- Вводим значение числа;
- Находим кнопку с символом корня на калькуляторе;
- Нажимаем на кнопку корня и вводим значение степени, если нужно;
- Получаем результат, который является корнем заданного числа.
Таким образом, использование калькуляторов для нахождения корня числа облегчает процесс вычисления и упрощает получение точного результата. Современные калькуляторы позволяют вычислять корни с заданной точностью, что особенно важно для научных и инженерных расчетов.