Биномиальное распределение - одно из важнейших распределений в теории вероятностей и статистике. Это дискретное распределение, которое моделирует число успехов в серии независимых и одинаково распределенных Бернуллиевских испытаний. В Python есть мощные инструменты для работы с биномиальным распределением, что позволяет анализировать и моделировать сложные вероятностные явления.
В этой статье мы предлагаем пошаговую инструкцию по использованию биномиального распределения в Python. Мы рассмотрим основные функции и методы модуля `scipy.stats`, который предоставляет широкие возможности для работы с распределениями случайных величин. Мы также приведем примеры кода и практические применения биномиального распределения.
Для начала, давайте разберемся с базовыми понятиями: вероятность успеха (или долю успехов) и число испытаний (или размер выборки). В биномиальном распределении вероятность успеха обычно обозначается символом `p`, а число испытаний - символом `n`. Используя эти параметры, мы можем вычислить вероятность получения определенного числа успехов в серии испытаний.
Биномиальное распределение в Python

Python предлагает удобные инструменты для работы с биномиальным распределением. В стандартной библиотеке Python есть модуль statistics, который содержит функции для расчета вероятности и статистических характеристик биномиального распределения.
Для использования библиотеки statistics вам понадобится установить Python на ваш компьютер и иметь предварительное представление о биномиальном распределении. Затем вы сможете использовать функции из модуля statistics для решения задач, связанных с биномиальным распределением.
К примеру, вы можете использовать функцию statistics.binom.pmf(x, n, p), чтобы вычислить вероятность получения x успехов в n независимых испытаниях с вероятностью успеха p.
Также, вы можете использовать функцию statistics.binom.cdf(x, n, p), чтобы вычислить вероятность получения не более x успехов в n независимых испытаниях с вероятностью успеха p.
Python позволяет вам легко использовать функции для работы с биномиальным распределением и проведения статистических анализов. Они предоставляют удобный способ решать задачи, связанные с биномиальным распределением, и получать точные и достоверные результаты.
Что такое биномиальное распределение?
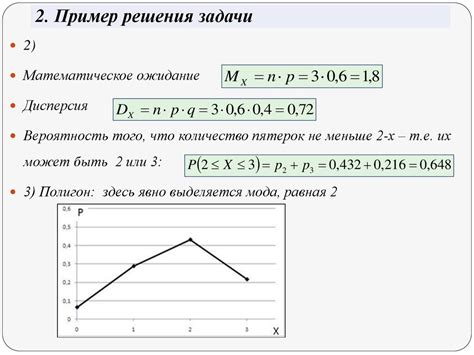
Биномиальное распределение определяется двумя параметрами: количество испытаний (n) и вероятность успеха в каждом испытании (p). Каждое испытание независимо от других и имеет одинаковую вероятность успеха.
Биномиальное распределение может быть полезным в различных областях, включая статистику, экспериментальные исследования, биологию и маркетинг. Например, можно использовать биномиальное распределение для моделирования вероятности успеха в серии испытаний, таких как бросание монеты, выборка случайных генов в популяции или конверсия веб-страницы.
Как использовать биномиальное распределение в Python?
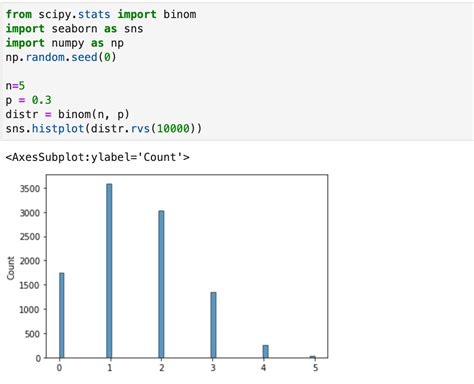
Для начала, нам потребуется импортировать необходимые модули:
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
Далее, мы можем создать объект биномиального распределения с помощью функции binom. В качестве аргументов передаем количество испытаний n и вероятность успеха p:
n = 10 # количество испытаний
p = 0.5 # вероятность успеха
dist = binom(n, p)
Мы можем использовать созданный объект для получения различных характеристик биномиального распределения. Например, чтобы получить вероятность выпадения определенного числа успехов, можем воспользоваться методом pmf (Probability Mass Function):
k = 5 # число успехов
prob = dist.pmf(k)
print("Вероятность получить", k, "успехов:", prob)
Мы также можем построить график вероятностей различных чисел успехов. Для этого используем функцию plot из библиотеки matplotlib.pyplot:
x = np.arange(0, n+1) # числа успехов
y = dist.pmf(x) # вероятности
plt.plot(x, y, 'bo', ms=8)
plt.vlines(x, 0, y, colors='b', lw=5, alpha=0.5)
plt.xlabel('Число успехов')
plt.ylabel('Вероятность')
plt.title('Биномиальное распределение')
plt.show()
На графике мы можем увидеть вероятности различного числа успехов в биномиальном распределении.
Таким образом, использование биномиального распределения в Python может быть достаточно простым и эффективным с помощью библиотеки scipy.stats. Мы можем создавать объекты биномиального распределения, вычислять вероятности и строить графики для визуализации распределения.
Примеры применения биномиального распределения в Python
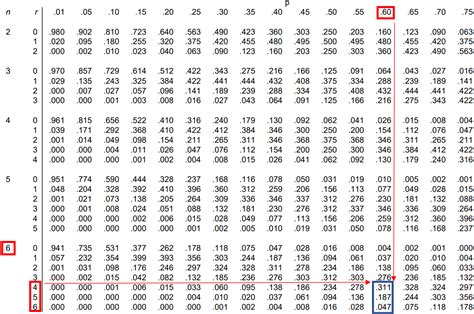
Биномиальное распределение широко применяется во множестве задач, где требуется оценить вероятность наступления события в серии независимых экспериментов. Вот несколько примеров его применения в Python:
| Пример | Описание |
|---|---|
| 1 | Оценка вероятности успеха при многократном повторении независимого эксперимента. |
| 2 | Моделирование процесса подбрасывания монеты и оценка вероятности получения определенного количества орлов или решек. |
| 3 | Анализ результатов A/B-тестирования для оценки эффективности нового метода. |
| 4 | Оценка вероятности повреждения конкретной части изделия на производстве при заданном количестве испытаний. |
| 5 | Моделирование распределения числа успехов в серии независимых испытаний для проведения статистического анализа. |
Эти примеры демонстрируют только небольшую часть возможностей биномиального распределения в Python. Оно может быть использовано в различных областях, таких как статистика, биология, экономика, маркетинг и другие. Использование Python для работы с биномиальным распределением позволяет проводить анализ данных и моделирование с высокой точностью и эффективностью.
Как оценить результаты с использованием биномиального распределения?
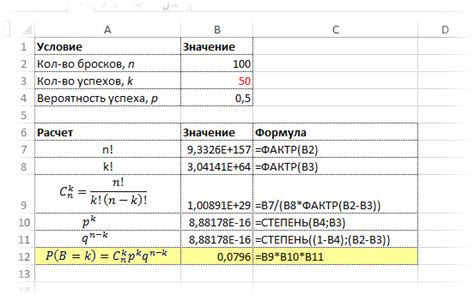
Биномиальное распределение предоставляет нам инструмент для оценки результатов в экспериментах, в которых возможны только два взаимоисключающих исхода: успех и неудача. Оно широко применяется в различных областях, таких как биология, медицина, экономика и маркетинг.
Для оценки результатов с использованием биномиального распределения необходимо знать два основных параметра: вероятность успеха (p) и число испытаний (n). Вероятность успеха представляет собой вероятность того, что исход будет положительным, а число испытаний определяет количество независимых экспериментов, которые будут проведены.
Чтобы оценить результаты, мы можем использовать функции библиотеки SciPy в Python, которые предоставляют нам возможность вычислить вероятность получения определенного количества успехов.
Например, если проводится маркетинговая кампания, и мы хотим оценить вероятность получения определенного количества кликов на рекламный баннер, мы можем использовать биномиальное распределение. Зная вероятность клика на баннер (p) и общее количество показов (n), мы можем использовать функцию binom.pmf() для оценки вероятности получения определенного количества кликов.
Биномиальное распределение также может быть полезно для оценки значимости различий между двумя группами. Например, если мы проводим эксперимент со сравнением эффективности двух новых лекарств, мы можем использовать биномиальное распределение для определения, есть ли статистически значимая разница в количестве пациентов, выздоровевших в каждой группе.
Важно отметить, что биномиальное распределение предоставляет только вероятностную оценку результатов и не гарантирует определенный исход. Однако оно является мощным инструментом для статистического анализа и оценки результатов в различных экспериментах.
Использование биномиального распределения в Python позволяет нам легко проводить анализ данных и получать результаты, которые помогут нам принять важные решения на основе статистической значимости.