Арксинус и арккосинус - это две важные тригонометрические функции, которые помогают решать различные задачи в математике, физике и инженерии. Эти функции являются обратными к синусу и косинусу соответственно и обладают рядом уникальных свойств и применений.
Арксинус, обозначаемый как arcsin(x) или sin-1(x), возвращает значение угла, чей синус равен x. Другими словами, если у нас есть синусовое значение x, мы можем использовать арксинус, чтобы найти угол, чей синус равен x. Функция арксинус определена в интервале от -π/2 до π/2 и может принимать значения от -1 до 1.
Арккосинус, обозначаемый как arccos(x) или cos-1(x), возвращает значение угла, чей косинус равен x. Также, как и арксинус, арккосинус функция определена в интервале от 0 до π и может принимать значения от -1 до 1. Арккосинус можно использовать для нахождения угла, чей косинус равен x.
Эти функции имеют множество применений в различных областях. Например, они могут быть использованы для решения треугольных задач, определения углов между векторами, анализа периодических колебаний и многого другого. Знание того, как использовать арксинус и арккосинус, может быть полезным в решении разнообразных задач, требующих работы с тригонометрическими функциями.
Арксинус и арккосинус: основные понятия
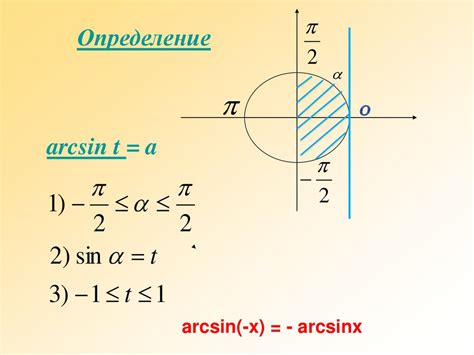
Арксинус обозначается как asin(x), где x - значение синуса, арккосинус - как acos(x), где x - значение косинуса. Область значений арксинуса ограничена от -π/2 до π/2, а область значений арккосинуса - от 0 до π.
Арксинус и арккосинус являются нелинейными функциями и могут использоваться в различных областях, таких как математика, физика, алгоритмы и т.д.
Применение арксинуса и арккосинуса в математике и физике
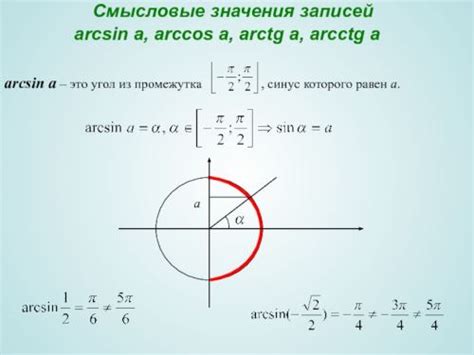
В математике, арксинус и арккосинус позволяют находить углы по заданным значениям синуса и косинуса. Например, если нам дано значение синуса угла, то с помощью арксинуса мы можем найти сам угол. Это особенно полезно при решении геометрических задач, таких как нахождение углов треугольника или определение координат точки на плоскости.
В физике, арксинус и арккосинус также широко используются. Они помогают в решении задач, связанных с гармоническими колебаниями и колебаниями в циклических процессах. Например, при изучении механических колебаний и электромагнитных волн, арксинус и арккосинус позволяют находить амплитуду колебаний, фазу и частоту.
Кроме того, арксинус и арккосинус применяются в статистике и вероятности. Они используются для преобразования вероятностей в углы и обратно, что полезно при анализе данных и построении математических моделей в различных областях науки.
В целом, арксинус и арккосинус имеют множество применений в различных областях науки и техники. Их использование позволяет решать разнообразные задачи и упрощать сложные математические расчеты. Поэтому понимание и умение применять арксинус и арккосинус являются важными навыками для успешного изучения и практического применения математики и физики.
Примеры использования арксинуса и арккосинуса

Пример 1:
Допустим, нам известно, что синус угла α равен 0,5. Чтобы найти значение угла α, используем арксинус:
α = arcsin(0,5)
Получим значение угла α, равное 30°.
Пример 2:
Предположим, нам известно, что косинус угла β равен -0,8. Чтобы найти значение угла β, используем арккосинус:
β = arccos(-0,8)
Получим значение угла β, равное 142°.
Пример 3:
Допустим, нам известно значение синуса угла γ, равное 1. Чтобы найти значение угла γ, используем арксинус:
γ = arcsin(1)
В данном случае, так как синус угла γ равен 1, угол γ будет равен 90°.
Таким образом, арксинус и арккосинус являются полезными математическими функциями, которые позволяют находить значения углов с использованием синуса и косинуса.