Бумага из ели является одним из самых популярных видов ручной бумаги благодаря своей натуральности и уникальному текстурному эффекту. Эта бумага имеет особую привлекательность и может использоваться для создания подарков, открыток, художественных работ и многого другого. Однако, процесс изготовления бумаги из ели может показаться сложным на первый взгляд. В данной статье мы предоставим вам пошаговую инструкцию о том, как сделать бумагу из ели своими руками.
Шаг 1: Сбор ели. Первым шагом в процессе создания бумаги из ели является сбор самого материала - свежих иголок, веточек и коры ели. Выберите здоровые ели с красивыми иголками, так как это будет влиять на качество бумаги. Собирайте материал в течение нескольких дней перед началом процесса изготовления бумаги, чтобы у вас было достаточно сырья.
Шаг 2: Подготовка материала. После сбора материала, отделите иголки от веток и коры, а затем разотрите их до состояния пасты. Для этого можно использовать ступку или блендер. Добавьте немного воды, чтобы получить консистенцию пасты. Затем перекладывайте полученную пасту в большую емкость и промойте ее, чтобы избавиться от лишних примесей и получить чистую целлюлозу.
Шаг 3: Процесс переработки. Для процесса переработки используйте специальные рамки для бумаги или самодельные рамки из дерева и сетки. Заносите пасту на рамку и равномерно распределите ее по всей поверхности с помощью шпателя. Затем аккуратно переворачивайте рамку так, чтобы бумага осталась на сетке. Оставьте бумагу на сетке до полного высыхания.
Продолжайте повторять шаги 2 и 3, пока не получите желаемое количество бумаги. Помните, что процесс изготовления бумаги из ели требует точности и терпения, поэтому не спешите и следуйте инструкциям. В результате вы получите красивую, натуральную бумагу из ели, которую можно использовать для различных творческих проектов.
Поступательное движение электронов в сплошных средах

Электроны – это заряженные частицы, которые обладают массой и имеют отрицательный заряд. В сплошных средах они могут свободно перемещаться под воздействием электрического поля. Поступательное движение электронов описывается законом Ома, который устанавливает пропорциональность между током и напряжением в схеме.
При поступательном движении электронов в сплошных средах они сталкиваются с атомами вещества, что вызывает их рассеяние. Такой процесс называется столкновительным рассеянием. Рассеяние электронов происходит из-за кулоновского взаимодействия электрона с положительно заряженным ядром и электронами других атомов. Вследствие столкновений, электроны изменяют свою траекторию и направление движения.
Степень рассеяния электронов в сплошной среде зависит от различных факторов, таких как концентрация примесей, температура, длина свободного пробега и энергия электронов. В некоторых случаях рассеяние электронов может быть значительным, что приводит к большому сопротивлению при прохождении тока через вещество.
Однако, в определенных условиях, электроны могут двигаться почти без рассеяния. Сферическая симметрия кристаллической решетки некоторых материалов может создать условия, при которых электроны испытывают минимальное влияние рассеяния и могут двигаться с постоянной скоростью. Это состояние называется мобильностью носителей заряда и играет важную роль в электронике.
Описание и принципы

В первую очередь необходимо собрать достаточное количество молодых еловых иголок. Рекомендуется собирать их весной или осенью, когда иголки находятся в наилучшем состоянии. Специалисты советуют выбирать иголки от здоровых елей, чтобы полученная бумага была качественной и долговечной.
Далее необходимо вымочить собранные иголки в воде, чтобы удалить с них лишние примеси и органические вещества. Это можно сделать, поместив иголки в большую емкость с водой и оставив на несколько дней.
После этого следует измельчить вымоченные иголки до состояния пасты. Для этого можно использовать блендер или специальные мельницы. Полученную массу следует разместить в большой емкости с водой и тщательно перемешать, чтобы получить равномерную смесь.
Затем с помощью сита следует отделить от полученной смеси лишние частицы и остатки. Чтобы ускорить процесс отделения, можно погрузить сито с массой в воду и аккуратно перемешивать. В результате на сите останутся только чистые волокна из еловых иголок.
Последний этап включает формовку и сушку бумаги. Для формовки можно использовать специальные формы или самодельные пресса. Полученную массу из волокон следует выложить на форму и аккуратно распределить по всей ее площади. Затем бумагу необходимо прессовать и оставить на сушку до полного высыхания.
Таким образом, изготовление бумаги из ели требует некоторых усилий, но результат стоит всех затрат. Полученная бумага будет экологически чистой, а сам процесс изготовления принесет массу удовольствия и удовлетворения от созидания чего-то своими руками.
Ферми-дираковское распределение электронов
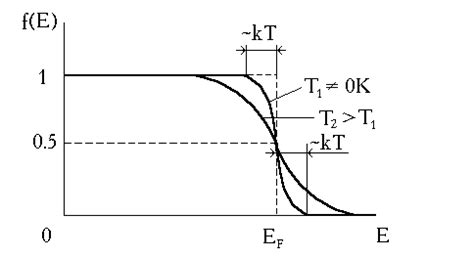
В квантовой физике существует понятие Ферми-дираковского распределения электронов, которое описывает вероятность нахождения электрона в определенном состоянии при заданной температуре. Это распределение названо в честь Инрико Ферми и Пауля Дирака, которые сделали ключевые открытия в области квантовой статистики и фермионов.
Ферми-дираковское распределение применяется для систем электронов с полуцелым спином, таких как электроны в металлах. Оно описывает, как заполняются энергетические уровни электронами, начиная с низших, при увеличении энергии. Ключевая особенность этого распределения - принцип запрета Паули, согласно которому электроны не могут находиться в одном и том же квантовом состоянии одновременно.
Ферми-дираковское распределение выражается следующей формулой:
- Каждому энергетическому состоянию соответствует определенное количество электронов.
- Вероятность нахождения электрона в состоянии с энергией E определяется распределением Ферми-Дирака:
- P(E) = 1 / (1 + exp((E - E_F) / (k_B * T)))
Это распределение позволяет определить занятые и свободные состояния электронов в системе. Уровень энергии, соответствующий энергии Ферми, разграничивает энергетические уровни на занятые (ниже) и свободные (выше).
Ферми-дираковское распределение электронов является основным инструментом для анализа электронных свойств материалов и для понимания процессов, происходящих в полупроводниках, металлах и других системах с электронами.
Дробное дифференцирование Аррениуса с распределением

Аррениусовская зависимость показывает, как скорость реакции зависит от температуры. Она формулируется следующим образом:
где k - скорость реакции, A - преэкспоненциальный множитель, Ea - активационная энергия, R - универсальная газовая постоянная, T - температура.
При использовании дробного дифференцирования Аррениусовской зависимости с распределением активационных энергий учитывается различное значение активационной энергии для каждого реакционного шага, что позволяет более точно описывать кинетику реакции. Распределение активационных энергий описывается функцией g(Ea), которая указывает, как часто встречаются различные значения активационной энергии в системе.
Математически дробное дифференцирование Аррениуса с распределением может быть записано следующим образом:
- Вычисление интеграла от преэкспоненциального множителя A гамма-функции Γ(1 - α)
- Умножение полученного значения на гамма-функцию Γ(α)
- Вычисление интеграла от распределения активационных энергий g(Ea) с показателем α
- Умножение полученного значения на скорость реакции k0 из Аррениусовской зависимости
- Произведение полученных значений из шагов 2, 3 и 4
Таким образом, дробное дифференцирование Аррениуса с распределением позволяет более точно описывать скорость химической реакции, учитывая различные значения активационной энергии в системе.
Невязки и степени свободы электрона
В теории твердого тела, невязкой называется разность между измеренным и теоретическим значением некоторой физической величины. Значение невязки может служить показателем качества модели или теории, используемой для описания данной величины.
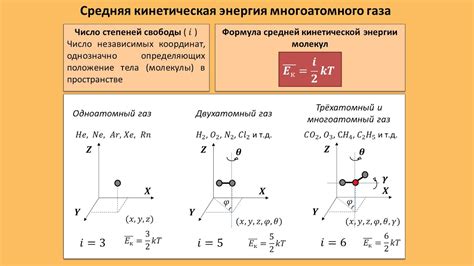
Степени свободы электрона – это способы, которыми электрон может двигаться в кристаллической решетке твердого тела. Степень свободы может быть связана с движением электрона в трехмерном пространстве, его спином или другими свойствами. Обычно степени свободы электрона изучаются при расчете его энергии и динамических свойств.
Взятые во внимание взаимодействия

При процессе изготовления бумаги из ели важно учитывать не только физические и химические свойства материалов, но и взаимодействия между ними. Различные этапы изготовления бумаги требуют внимания к основным взаимодействиям, которые происходят.
Механическое взаимодействие: Вначале, при измельчении ели, необходимо обеспечить эффективную раздробление материала для получения волокон нужной длины. Затем, взаимодействие между волокнами происходит во время формирования листа бумаги, когда волокна выстраиваются в сетку и образуют основу листа.
Химическое взаимодействие: Для получения бумаги из ели необходимо сделать волокна более податливыми и обработать их таким образом, чтобы они легче связывались друг с другом. Для этого применяются различные химические реактивы, такие как растворы щелочей и кислот, которые помогают расщепить лигнин - вещество, делающее волокна жесткими и неподатливыми.
Тепловое взаимодействие: В процессе отжига и сушки бумаги из ели происходит термическое воздействие на волокна, которое способствует их связыванию и приданию прочности. Возможное разрушение волокон при этом этапе может привести к потере качества бумаги.
Учитывая все эти взаимодействия, можно достичь наилучшего результата при изготовлении бумаги из ели. Каждое взаимодействие должно быть тщательно контролируемо и оптимизировано, чтобы получить бумагу высокого качества.
Дискретные диффузионные модели электрона в вакууме
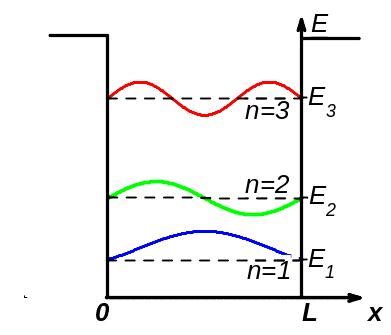
Вакуумные диффузионные модели электрона используются для изучения и описания процессов, связанных с передвижением электрона в вакууме. Они представляют собой дискретные модели, в которых электрон рассматривается как частица, перемещающаяся от одного узла сетки к другому.
В основе диффузионных моделей лежит предположение о том, что процессы диффузии электрона в вакууме можно описать с помощью случайных перемещений между соседними узлами сетки. Такой подход позволяет учесть вероятностные характеристики перемещения электрона и рассчитать его конечное положение в вакууме.
Диффузионные модели электрона обычно строятся на основе сеточной структуры, в которой каждый узел представляет собой маленький объем вакуума. Между соседними узлами существуют различные типы связей, которые определяют вероятность перемещения электрона от одного узла к другому.
| Тип связи | Вероятность |
|---|---|
| Прямая связь | Высокая |
| Диагональная связь | Средняя |
| Боковая связь | Низкая |
Когда электрон перемещается от одного узла к другому, для каждой связи определяется вероятность перемещения. Эта вероятность зависит от типа связи и может быть разной для разных узлов сетки. Таким образом, через каждую связь происходит случайный выбор направления движения электрона.
Использование дискретных диффузионных моделей электрона позволяет проводить численные расчеты и описывать сложные процессы в вакууме, такие как диффузия электронов от источника к подложке. Такие модели находят применение в различных областях науки и техники, включая полупроводниковую электронику, наноматериалы и нанотехнологии.
Ферми-дираковское распределение электронов

Согласно принципу исключения Паули, каждое энергетическое состояние может содержать только одного электрона. Ферми-дираковское распределение учитывает это ограничение и представляет собой функцию, которая показывает вероятность наличия электрона в определенном энергетическом состоянии.
Ферми-дираковское распределение имеет следующий вид:
f(E) = 1 / (exp((E - EF) / kB T) + 1),
где f(E) - вероятность наличия электрона в энергетическом состоянии E, EF - энергия Ферми (энергия электрона при абсолютном нуле), kB - постоянная Больцмана, T - температура системы.
В зависимости от значений энергии и температуры, ферми-дираковское распределение может представлять собой различные формы. При нулевой температуре все энергетические состояния ниже энергии Ферми заполняются электронами, а все состояния выше энергии Ферми остаются незанятыми.
Когда температура системы возрастает, вероятность нахождения электронов в более высокоэнергетических состояниях увеличивается, и распределение становится более плоским.
Ферми-дираковское распределение является основой для объяснения ряда явлений, таких как электрический ток в металлах и полупроводниках, электронная проводимость и многие другие свойства электронных систем.
