График функции обратно пропорциональности является одним из наиболее распространенных и интересных способов визуализации взаимосвязи между двумя переменными в математике. Такая функция описывает ситуацию, когда одна величина увеличивается, а другая уменьшается пропорционально с первой. Такой вид функции можно встретить в различных областях, от физики до экономики.
Чтобы построить график функции обратно пропорциональности, необходимо знать ее уравнение. Обычно оно имеет вид y = k/x, где y - зависимая переменная, x - независимая переменная, а k - постоянная величина. Значение k определяет наклон графика и его положение на координатной плоскости.
Для построения графика нам понадобится система координат - оси Ox и Oy. Ось Ox представляет собой горизонтальную линию, на которой откладываются значения независимой переменной x. Ось Oy - вертикальная линия, на которой откладываются значения зависимой переменной y. Начало координат обозначается точкой O.
Теперь, имея уравнение функции и систему координат, мы можем построить график путем последовательного откладывания точек на координатной плоскости. Для этого выбираем несколько значений независимой переменной x, подставляем их в уравнение и находим соответствующие значения зависимой переменной y. Затем отмечаем эти точки на графике и соединяем их линией.
Что такое обратно пропорциональные функции?

Математические обратно пропорциональные функции могут быть представлены в виде уравнения y = k/x, где x и y - две переменные, а k - постоянный коэффициент. Здесь, если значение x увеличивается, значение y уменьшается, и наоборот.
График обратно пропорциональной функции представляет собой гиперболу, которая имеет особую форму - две ветви, которые приближаются к двум осям координат.
Обратно пропорциональные функции широко используются в различных областях, таких как физика, экономика, статистика и т.д. Например, в физике обратно пропорциональные функции могут описывать законы сохранения, где одна величина увеличивается, а другая уменьшается в соответствии с законом сохранения общей энергии или стоимости.
Как определить обратно пропорциональную функцию?

Для определения обратно пропорциональной функции необходимо выполнить следующие шаги:
- Составьте таблицу значений, где одна колонка будет содержать значения одной величины, а другая колонка - значения другой величины.
- Постройте график, где оси координат представляют значения обеих величин.
- Изучите график и таблицу значений. Если значения одной величины увеличиваются, а значения другой величины уменьшаются (и наоборот), то функция обратно пропорциональная.
Если функция обратно пропорциональная, то ее можно записать в виде y = k/x, где k - постоянное число. Здесь y - значение одной величины, x - значение другой величины.
Например, если имеется величина x, зависящая от величины y обратно пропорционально, то уравнение будет выглядеть как y = (k/x), где k - постоянное число.
| x | y |
|---|---|
| 1 | 6 |
| 2 | 3 |
| 3 | 2 |
| 4 | 1.5 |
Построим график для этих значений:
| x | y | График | ||
|---|---|---|---|---|
| 1 | 6 | . | . | . |
| 2 | 3 | . | . | . |
| 3 | 2 | . | . | . |
| 4 | 1.5 | . | . | . |
Из графика видно, что значения одной величины увеличиваются, а значения другой величины уменьшаются, следовательно, функция обратно пропорциональная.
Таким образом, определить обратно пропорциональную функцию можно путем построения графика и анализа значений обеих величин. Если значения одной величины увеличиваются, а значения другой величины уменьшаются (и наоборот), то функция является обратно пропорциональной.
Как построить график обратно пропорциональной функции?

Для построения графика обратно пропорциональной функции необходимо выполнить следующие шаги:
- Выберите две переменные, между которыми существует обратная пропорция. Обозначим их как x и y.
- Составьте таблицу значений, где в столбце x будут указаны различные значения переменной x, а в столбце y будут соответствующие значения переменной y.
- Вычислите значения переменной y используя формулу обратно пропорциональной функции: y = k/x, где k - постоянная пропорциональности. Значения k можно выбрать произвольно.
- Отметьте на координатной плоскости полученные точки. Постройте график функции, соединив точки прямой линией.
- Продолжите график в обе стороны до тех пор, пока функция не достигнет оси x или y.
График обратно пропорциональной функции будет иметь вид гиперболы. Он будет проходить через точку (k, 1), где k - выбранная постоянная пропорциональности.
График обратно пропорциональной функции важен для визуализации зависимости двух величин, и может быть использован для анализа данных, принятия решений или предсказания тенденций.
Некоторые примеры обратно пропорциональных функций

Например, функция y = k/x, где k - постоянное значение, представляет собой обратно пропорциональную функцию. График этой функции будет гиперболой, которая имеет две ветви, проходящие через начало координат.
Еще одним примером может служить функция y = k/x^2, где k - постоянное значение. В этом случае график функции будет иметь форму параболы, которая открывается вниз. Чем больше значение x, тем меньше значение y, что показывает обратную пропорциональность между ними.
Если рассмотреть функцию y = k√x, где k - постоянное значение, то график будет представлять собой кривую, которая начинается в начале координат и стремительно возрастает при уменьшении значения x. Здесь также наблюдается обратная пропорциональность между переменными.
Это лишь некоторые примеры обратно пропорциональных функций и их графиков. В реальных приложениях и задачах могут быть использованы и другие типы обратно пропорциональных зависимостей, что позволяет моделировать различные ситуации и явления.
Как объяснить график обратно пропорциональной функции?

Обратно пропорциональные функции могут быть представлены уравнением вида y = k/x, где y и x - переменные, а k - постоянный коэффициент. График такой функции представляет собой гиперболу.
Чтобы легче понять, как объяснить график обратно пропорциональной функции, можно рассмотреть конкретный пример. Например, если мы рассматриваем зависимость между временем и скоростью движения, то при увеличении скорости, время, затраченное на преодоление расстояния, будет уменьшаться.
Пример:
Пусть у нас есть задача: один автомобиль движется со скоростью 60 км/ч, а второй со скоростью 80 км/ч. Необходимо определить время, которое эти автомобили затратят на преодоление одного и того же расстояния.
Использование обратно пропорциональной функции поможет нам решить эту задачу. В данном случае, мы можем записать уравнение времени в виде:
t = k/v
где t - время, k - постоянный коэффициент и v - скорость.
Подставив значения из задачи и решив уравнение, мы получим:
t1 = k/60
t2 = k/80
Таким образом, видно, что время, которое затратит автомобиль с большей скоростью, будет меньше, что подтверждает обратную пропорциональность между временем и скоростью.
На графике обратно пропорциональной функции это будет выглядеть как гипербола, где точки, представляющие разные значения переменных, будут расположены на кривой линии.
Изучение графика обратно пропорциональной функции и его объяснение помогут лучше понять и анализировать зависимости между переменными и применять их в реальных задачах.
Как использовать график обратно пропорциональной функции в анализе данных?

Для построения графика обратно пропорциональной функции необходимо определить математическую формулу этой функции, которая имеет вид y = k/x, где k - постоянная величина, а x и y - переменные.
Построение графика начинается с выбора значения переменной x, которое представляет собой независимую переменную в данной функции. Далее, используя математическую формулу, можно вычислить соответствующее значение y. Повторяя эту операцию для различных значений x, можно получить набор пар значений, представленных координатами на плоскости.
После получения набора координат, можно построить график, отображающий обратно пропорциональную зависимость между переменными x и y. Обычно график представляется с помощью системы координат, где по оси x откладываются значения переменной x, а по оси y - значения переменной y. Затем, используя полученные точки данных, соединяют их линией или графиком, чтобы наглядно продемонстрировать обратную зависимость.
График обратно пропорциональной функции может быть полезен при анализе данных, так как позволяет определить, как изменение переменной x влияет на переменную y. Кривая графика может указывать на существование обратной зависимости между переменными и помочь в изучении данной взаимосвязи. Например, при увеличении значения x, значение y будет уменьшаться, и наоборот.
Кроме того, график обратно пропорциональной функции может предоставить информацию о других характеристиках зависимости, таких как точки пересечения с осями координат (например, нулевой точки) или асимптоты. Таким образом, анализ графика может дать полное представление о данной обратной пропорциональной зависимости.
Практические рекомендации по построению графика обратно пропорциональной функции
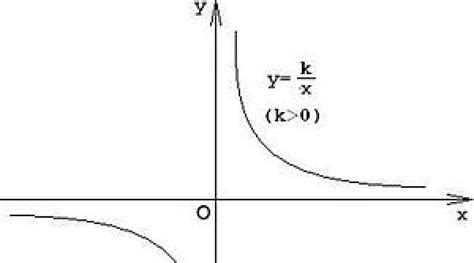
При построении графика обратно пропорциональной функции важно иметь ясное представление о свойствах такого типа функций. Обратно пропорциональная функция представляет собой математическую модель, в которой одна переменная обратно пропорциональна другой, то есть при увеличении одной переменной величина другой уменьшается и наоборот.
Для построения графика обратно пропорциональной функции, необходимо следовать следующим практическим рекомендациям:
- Определить область значений переменных: В начале работы с функцией необходимо определить область значений переменных, то есть диапазон значений, в пределах которого будут находиться значения переменных. Это поможет ограничить пространство для построения графика.
- Построить оси координат: Построение осей координат является основой для построения графика функции. Горизонтальная ось (ось абсцисс) представляет собой ось переменной, которая увеличивается слева направо. Вертикальная ось (ось ординат) представляет собой ось переменной, которая увеличивается снизу вверх.
- Выбрать несколько значений и построить точки: Выберите несколько различных значений для каждой переменной и постройте соответствующие точки на графике. Необходимо выбрать значения, которые находятся в области значений переменных, определенной на первом шаге. Построение точек позволит получить первое представление о форме графика.
- Соединить точки прямой: После построения точек на графике, соедините их прямой линией. График обратно пропорциональной функции представляет собой гиперболу, которая имеет форму кривой, приближающейся к осям координат.
- Обозначить особые точки: Если есть особые точки или значения переменных, которые имеют особое значение для функции, необходимо обозначить их на графике. Например, если есть точка пересечения с осями координат или точка экстремума.
Следуя этим практическим рекомендациям, вы сможете построить график обратно пропорциональной функции и наглядно представить зависимость между переменными. Это поможет в изучении и анализе таких функций, а также в применении их в реальных ситуациях.