Окружность – это одно из фундаментальных геометрических понятий, которое находит широкое применение в различных областях знаний и практической деятельности. Одна из важных характеристик окружности – это ее диаметр. Знание диаметра позволяет точно определить размеры окружности и проводить необходимые вычисления. В данной статье мы рассмотрим, как найти диаметр окружности по известным параметрам – хорде и углу.
Для начала, давайте определимся с понятиями. Хорда – это отрезок, соединяющий две точки на окружности. Угол – это геометрическая фигура, образованная двумя лучами с общим началом. Теперь рассмотрим, каким образом можно определить диаметр окружности по этим параметрам.
Для расчета диаметра по хорде и углу используется теорема проекций на хорду и угол, которая устанавливает зависимость между диаметром окружности и ее хордой. Согласно этой теореме, проекция хорды на диаметр окружности равна половине проекции хорды на угол, образованный этой хордой.
Что такое хорда и угол в окружности?

Угол: Угол в окружности - это угол, вершина которого находится на окружности, а стороны проходят через центр. Угол может быть как острый, так и тупой. Угол в окружности, который равен 90 градусов, называется прямым углом.
Изучение хорды и угла в окружности является важным при решении задач связанных с геометрией и геометрическими преобразованиями. Понимание этих понятий поможет вам вычислить диаметр окружности, основываясь на длине хорды и измерении угла. Зная значения хорды и угла, можно поменяться и найти другие значения, такие как радиус, длина окружности и площадь круга.
Зачем нужно знать диаметр окружности?
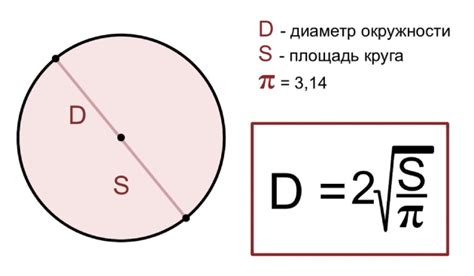
Вот несколько причин, почему знание диаметра окружности является полезным:
- Вычисление длины окружности: диаметр является основным параметром для определения длины окружности. Для удобства, длина окружности определяется через пи, равное приблизительно 3,14. Формула для вычисления длины окружности: длина = диаметр * π.
- Нахождение площади круга: диаметр также является необходимым параметром для вычисления площади круга. Формула для вычисления площади круга: площадь = π * (диаметр/2)^2.
- Определение касательной: зная диаметр окружности, можно определить касательную к окружности в заданной точке. Касательная к окружности является прямой линией, которая касается окружности только в одной точке.
- Измерение отрезков: диаметр можно использовать для измерения различных отрезков на окружности, таких как хорда или радиус. Это помогает в решении различных геометрических задач, таких как построение треугольников и секущих линий.
Зная диаметр окружности, вы сможете с легкостью решать геометрические задачи, связанные с окружностями, а также применять их в практических сферах, таких как инженерия, архитектура и дизайн.
Шаг 1: Измерьте длину хорды

Уверенно и аккуратно положите инструмент на хорду, начиная от одной точки на окружности и измерьте длину до второй точки. Запишите полученное значение в сантиметрах или дюймах.
Важно помнить: Чтобы получить точные результаты, измерение длины хорды должно быть выполнено с учетом возможных погрешностей при использовании измерительного инструмента.
Примечание: Если хорда не является прямой, а изогнутой, убедитесь в том, что вы измеряете длину самой короткой прямой линии между двумя точками на окружности.
Выбор способа измерения

Перед тем как начать измерение диаметра окружности по хорде и углу, важно определиться со способом, который будет наиболее удобным и точным для вас. Существует несколько различных способов измерения диаметра окружности, и выбор каждого способа зависит от доступных инструментов, точности, которую вы хотите достичь, и вашего уровня опыта. Вот несколько популярных способов измерить диаметр окружности:
- Измерение с помощью линейки: Самый простой и доступный способ измерения диаметра окружности - использование обычной линейки. Укажите хорду на окружности и измерьте ее длину с помощью линейки. Затем используйте формулу для вычисления диаметра.
- Измерение с помощью мерного ленты: Если хорда слишком длинная для обычной линейки, то можно использовать мерную ленту. Проведите ленту вдоль хорды окружности, проходящей через центр, и измерьте длину хорды. Затем используйте формулу для вычисления диаметра.
- Измерение с помощью штангенциркуля: Штангенциркуль - это инструмент с двумя подвижными челюстями, который используется для измерения длины и диаметра различных предметов. Расставьте челюсти штангенциркуля на хорде окружности, измерьте длину хорды и вычислите диаметр с помощью формулы.
- Измерение с помощью специализированного инструмента: Существуют специализированные инструменты, такие как спидиометр, которые могут использоваться для измерения диаметра окружности. Данные инструменты предназначены специально для этой цели и обеспечивают более точные измерения.
Важно помнить, что выбор способа измерения диаметра окружности будет зависеть от конкретных условий и требований. Если у вас возникли сомнения или вопросы, рекомендуется проконсультироваться с опытным специалистом или использовать более точный инструмент.
Приближенное измерение хорды

В некоторых случаях точное измерение длины хорды может быть затруднено, особенно если у вас нет специального инструмента или программы для измерения. Однако, можно использовать некоторые приближенные методы для определения приближенной длины хорды.
Вот несколько простых шагов, которые помогут вам приближенно измерить хорду окружности:
Установите точки начала и конца хорды. На окружности отметьте две точки, которые будут служить началом и концом вашей хорды. Обозначьте их как точки A и B соответственно.
Измерьте расстояние между точками. Используйте линейку или другой инструмент для измерения расстояния между точками A и B. Запишите это значение в сантиметрах.
Найдите оценочное значение диаметра. Используйте следующую формулу для вычисления оценочного значения диаметра окружности: диаметр = длина хорды / sin(угол между хордой и центром окружности). Угол должен быть выражен в радианах.
Полученное оценочное значение диаметра является приближенным и может содержать небольшую погрешность. Этот метод подходит для определения примерного значения диаметра, но для точных результатов рекомендуется использовать специальные инструменты или программы.
Помните, что это лишь один из способов приближенного измерения хорды окружности. Для более точных результатов всегда стоит прибегать к специализированным инструментам или методам.
Шаг 2: Найдите центральный угол
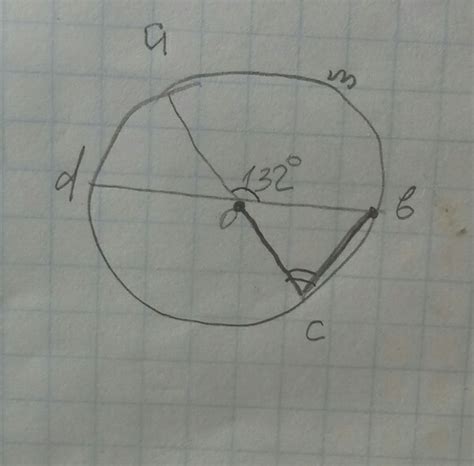
Чтобы найти диаметр окружности по хорде и углу, сначала нужно найти центральный угол. Центральный угол образуется дугой между концами хорды.
Для этого можно использовать теорему, которая гласит: "Центральный угол равен углу, образованному касательной, проведенной из одного из концов хорды, и радиусом, перпендикулярным к хорде."
Чтобы найти этот угол, вам понадобится либо транспортир, либо знание геометрии.
Если угол измеряется в градусах, необходимо использовать транспортир для измерения угла между касательной и радиусом. Если угол задан в радианах, измерять его не обязательно.
В результате, вы получите значение центрального угла, которое будет использоваться на следующем шаге для нахождения диаметра окружности.
Выбор метода поиска угла
При поиске диаметра окружности по хорде и углу необходимо выбрать подходящий метод для определения значения угла. В данном случае есть несколько возможных подходов:
1. Теорема о центральном угле.
Этот метод основан на теореме, которая гласит, что центральный угол, опирающийся на ту же хорду, равен половине величины угла, который охватывает эту хорду. Для применения данного метода необходимо найти угол, опирающийся на заданную хорду и имеющий ту же вершину, что и центр окружности. Затем найденная величина делится пополам для получения значения искомого угла.
2. Радианная мера угла.
Этот метод основан на использовании радианной меры угла, которая определяется как отношение длины дуги окружности к радиусу. В данном случае необходимо найти длину хорды, используя заданный угол и диаметр окружности. Затем найденная величина делится на половину диаметра, чтобы получить значение угла в радианах.
3. Тригонометрические функции.
Этот метод основан на использовании тригонометрических функций, таких как синус и косинус. В данном случае необходимо найти значение синуса или косинуса заданного угла и использовать его в уравнении, связывающем хорду, угол и радиус окружности. Затем решается полученное уравнение для определения значения искомого угла.
4. Использование геометрических свойств окружности.
Этот метод основан на применении геометрических свойств окружности, таких как равентсво углов при пересечении хорды и радиуса. Для применения данного метода необходимо использовать известные значения хорды и угла, а также свойства окружности, чтобы составить и решить систему уравнений для определения значения искомого угла.
Выбор метода определяется условиями поставленной задачи и имеющимися данными. Каждый метод имеет свои преимущества и недостатки, и правильный выбор метода позволит более точно определить значение искомого угла в заданной ситуации.
Применение тригонометрических функций для нахождения угла
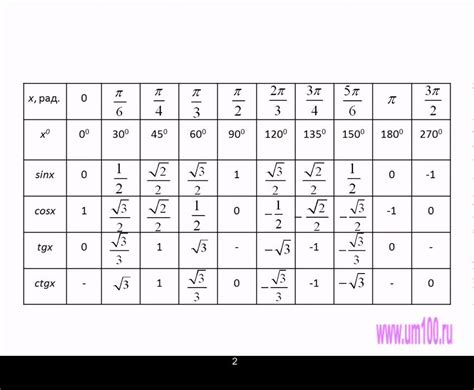
Для нахождения угла в геометрии, связанного с хордой и диаметром окружности, используются тригонометрические функции. Тригонометрические функции основаны на соотношениях между сторонами и углами в прямоугольном треугольнике.
Для нахождения угла при известном радиусе и хорде окружности, можно использовать функцию синус. Синус угла равен отношению длины противолежащего катета к длине гипотенузы прямоугольного треугольника. Применение синуса позволяет нам определить значение угла, исходя из известных величин. Формула для вычисления используемая для этого:
sin(угол) = (0.5 * хорда) / радиус
Решая эту формулу, мы можем найти значение угла.
Таким образом, применение тригонометрических функций, таких как синус, позволяет нам находить значения углов, исходя из известных величин, таких как радиус и хорда окружности.