Окружность - это одна из самых простых геометрических фигур, которая состоит из всех точек в плоскости, находящихся на одинаковом расстоянии от центра. Окружность может быть описана различными способами, в том числе указывая ее радиус, площадь или периметр.
Если у вас есть задача найти радиус окружности, зная ее площадь и периметр, то это можно сделать довольно просто и быстро, используя соответствующие формулы.
Для начала, давайте вспомним основные формулы, связанные с окружностью. Площадь окружности можно найти, используя формулу S = π * r^2, где S - площадь, π - математическая константа (приблизительно равная 3,14) и r - радиус окружности. Периметр окружности можно найти по формуле P = 2 * π * r, где P - периметр.
Итак, если у вас есть известная площадь и периметр окружности, вы можете легко найти радиус, просто подставляя значения в соответствующие формулы и решая уравнения. Например, чтобы найти радиус по известной площади и периметру, необходимо сначала выразить радиус через площадь и подставить его в формулу для периметра.
Формула для расчета радиуса окружности по площади
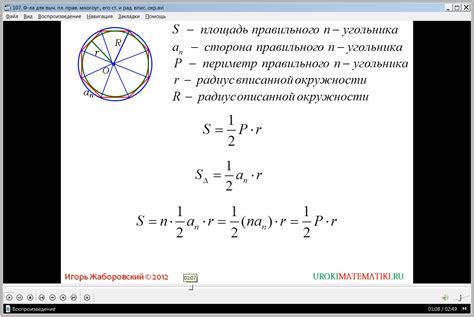
Для расчета радиуса окружности по площади можно использовать следующую формулу:
- Найти квадратный корень из площади окружности. Это позволит получить значение длины окружности.
- Разделить длину окружности на 2π (число Пи).
Таким образом, формула для расчета радиуса окружности будет выглядеть следующим образом:
Радиус = √(площадь / π)
Эта формула позволяет быстро и просто найти радиус окружности по известной площади.
Формула для расчета радиуса окружности по периметру
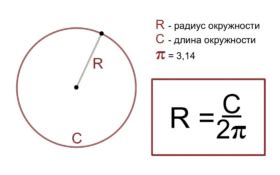
Для того чтобы найти радиус окружности по ее периметру, можно воспользоваться следующей формулой:
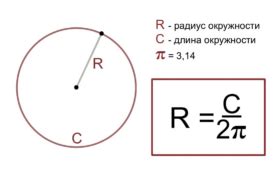
Радиус = Периметр / (2 * π)
Где:
- Радиус - это расстояние от центра окружности до ее границы;
- Периметр - это сумма длин всех сторон окружности;
- π (пи) - это математическая константа, примерное значение которой равно 3.14159.
Таким образом, чтобы найти радиус окружности по ее периметру, необходимо разделить периметр на два и затем получившееся значение поделить на π.
Например, если периметр окружности равен 20 единицам, то радиус можно найти следующим образом:
Радиус = 20 / (2 * 3.14159)
Результатом этого вычисления будет значение радиуса окружности.
Используя данную формулу, можно быстро и просто найти радиус окружности по ее периметру.
Примеры решения задачи
Рассмотрим несколько примеров решения задачи на нахождение радиуса окружности по известным площади и периметру.
Пример 1:
| Данные | Формула | Расчет |
|---|---|---|
| Площадь (S) | S = π * r^2 | Подставляем известные значения: |
| Периметр (P) | P = 2 * π * r | Подставляем известные значения: |
| S = (P^2) / (4 * π) | Подставляем известные значения: | |
| r^2 = (P^2) / (4 * π) | Решаем уравнение: | |
| r = sqrt((P^2) / (4 * π)) | Вычисляем радиус: |
Пример 2:
| Данные | Формула | Расчет |
|---|---|---|
| Площадь (S) | S = π * r^2 | Подставляем известные значения: |
| Периметр (P) | P = 2 * π * r | Подставляем известные значения: |
| S = (P^2) / (4 * π) | Подставляем известные значения: | |
| r^2 = (P^2) / (4 * π) | Решаем уравнение: | |
| r = sqrt((P^2) / (4 * π)) | Вычисляем радиус: |
Пример 3:
| Данные | Формула | Расчет |
|---|---|---|
| Площадь (S) | S = π * r^2 | Подставляем известные значения: |
| Периметр (P) | P = 2 * π * r | Подставляем известные значения: |
| S = (P^2) / (4 * π) | Подставляем известные значения: | |
| r^2 = (P^2) / (4 * π) | Решаем уравнение: | |
| r = sqrt((P^2) / (4 * π)) | Вычисляем радиус: |
Преимущества вычисления радиуса окружности по площади
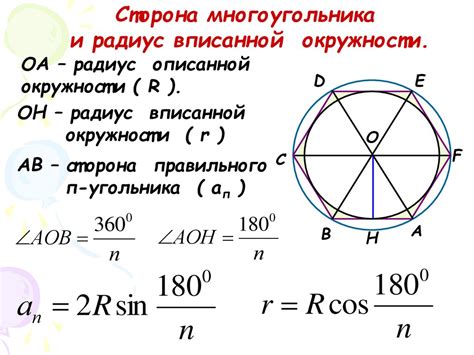
1. Простота вычислений
Вычисление радиуса окружности по площади основано на известной формуле: r = √(S / π), где r - радиус окружности, S - площадь окружности, а π - математическая константа.
Эта формула позволяет получить значение радиуса непосредственно из известной площади, без необходимости проведения дополнительных измерений или вычислений.
2. Экономия времени и усилий
Вычисление радиуса окружности по площади позволяет быстро получить геометрические параметры данной фигуры без необходимости выполнения сложных математических операций или продолжительных измерений.
Это особенно актуально в ситуациях, когда требуется оперативно определить радиус окружности, например, в инженерных и строительных задачах, при проектировании круглых объектов или при выполнении школьных заданий.
3. Универсальность применения
Метод вычисления радиуса окружности по площади применим не только для окружностей, но и для различных фигур с окружностями в качестве составной части, например, для сегментов, окружностей внутри круга или окружностей на плоскости.
Таким образом, вычисление радиуса окружности по известной площади является удобным и эффективным методом для определения геометрических параметров данной фигуры, обладающим простотой вычислений, экономией времени и универсальностью применения.
Преимущества вычисления радиуса окружности по периметру
Одним из главных преимуществ данного подхода является его простота. Для вычисления радиуса окружности по периметру не требуется решать сложные уравнения или проводить длительные математические вычисления. Зная значение периметра, можно сразу же приступить к вычислению радиуса.
Кроме того, этот метод предоставляет множество практических применений. Вычисление радиуса окружности по периметру может использоваться в различных областях, включая строительство, инженерию, архитектуру и геометрию. Например, при планировке участка или разработке проекта здания, знание радиуса окружности позволяет грамотно распределить пространство и определить оптимальные размеры конструкций.
Таким образом, вычисление радиуса окружности по периметру является надежным и удобным способом определения размеров геометрической фигуры. Этот метод обладает простотой и широким спектром практических применений, что делает его полезным инструментом при решении различных задач.