Вычисление периметра, площади и стороны – весьма полезные навыки, которые могут быть применены в повседневной жизни. Независимо от того, занимаетесь ли вы строительством, дизайном, математикой или просто хотите решить задачу, знание этих формул будет крайне полезно.
Периметр – это сумма длин всех сторон фигуры. Чтобы вычислить периметр, необходимо сложить длины всех сторон. Например, если у вас есть прямоугольник со сторонами 4 и 5, периметр будет равен 4 + 4 + 5 + 5 = 18. Просто и легко, не так ли?
Площадь – это мера площади поверхности фигуры. Для вычисления площади различных фигур существуют разные формулы. Например, для прямоугольника площадь равна произведению длины и ширины: 4 * 5 = 20. А для треугольника площадь можно вычислить по формуле: (основание * высота) / 2.
Вычисление стороны – это нахождение значения длины отдельной стороны фигуры. Это может быть полезно, когда у вас есть информация о других сторонах или других параметрах фигуры. Например, для нахождения стороны квадрата, если известна его площадь, нужно извлечь квадратный корень из площади.
В этой статье мы рассмотрели несколько примеров вычисления периметра, площади и стороны различных фигур. Надеемся, что наши полезные советы помогут вам легко и быстро решить такие задачи и применить полученные знания на практике.
Периметр, площадь и сторона: простые шаги для вычисления
Вычисление периметра, площади и стороны фигуры может показаться сложным, но на самом деле это достаточно просто. В этой статье мы рассмотрим несколько шагов, которые помогут вам с легкостью решить эти задачи.
Вычисление периметра
Периметр - это сумма всех сторон фигуры. Для вычисления периметра прямоугольника или квадрата, достаточно сложить длины всех его сторон. Например, если у прямоугольника стороны равны 4 и 6, то периметр будет равен 4 + 4 + 6 + 6 = 20.
Для вычисления периметра треугольника, сложите длины всех его сторон. Например, если длины сторон треугольника равны 5, 7 и 9, то периметр будет равен 5 + 7 + 9 = 21.
Вычисление площади
Площадь - это количество квадратных единиц, занимаемых фигурой. Для вычисления площади прямоугольника, умножьте длину его стороны на ширину. Например, если у прямоугольника длина 5 и ширина 3, то площадь будет равна 5 * 3 = 15.
Для вычисления площади круга, используйте формулу: S = π * r^2, где S - площадь, π - число Пи (приблизительно равно 3.14), r - радиус круга. Например, если радиус круга равен 2, то площадь будет равна 3.14 * 2^2 = 12.56.
Вычисление стороны
Для вычисления стороны прямоугольника или квадрата, достаточно знать его периметр. Если периметр квадрата равен 20, то каждая его сторона будет равна 20/4 = 5.
Для вычисления сторон треугольника, используйте теорему Пифагора, если известны длины двух сторон. Например, если известны длины сторон 3 и 4, то третья сторона может быть вычислена по формуле: с = sqrt(a^2 + b^2), где c - третья сторона, a и b - длины двух известных сторон. Таким образом, с = sqrt(3^2 + 4^2) ≈ 5.
Вычисление периметра, площади и стороны фигур может быть выполнено с помощью нескольких простых шагов. При необходимости, используйте формулы и теоремы, чтобы получить более точные результаты. Запомните эти простые шаги и решайте задачи по геометрии с легкостью!
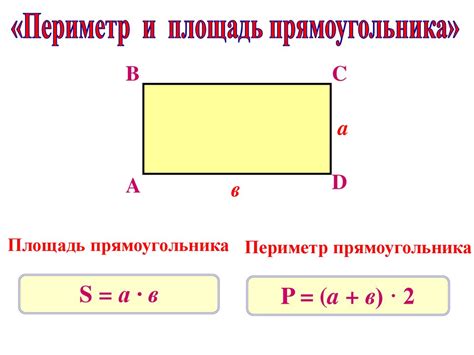
Как вычислить периметр
Для прямоугольника периметр вычисляется по формуле: P = 2(a + b), где a и b - длины сторон прямоугольника.
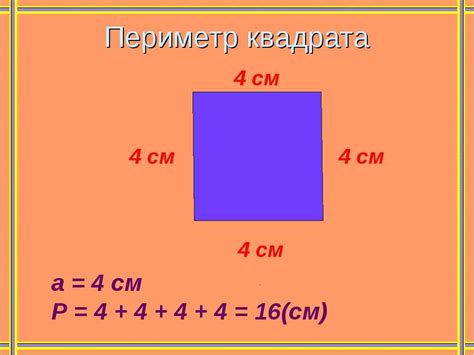
Если у вас есть квадрат, то его периметр можно найти умножив длину стороны на 4: P = 4a, где a - длина стороны квадрата.
Для треугольника, можно найти периметр, просуммировав длины всех трех сторон: P = a + b + c, где a, b и c - длины сторон треугольника.
У круга периметр называется окружностью. Периметр окружности можно найти по формуле: P = 2πr, где π - математическая константа, равная примерно 3.14159, а r - радиус окружности.
Теперь, когда вы знаете основные формулы для вычисления периметра различных фигур, вам будет легче решать задачи и находить периметр любой желаемой фигуры.
Как вычислить площадь
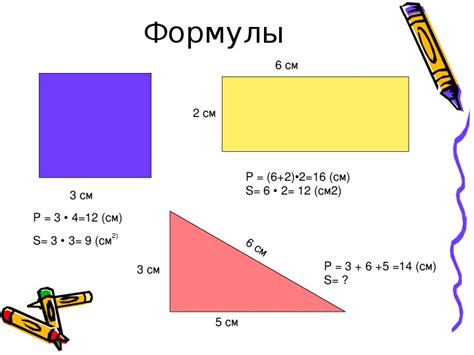
Для вычисления площади различных фигур существует ряд формул и методов. Рассмотрим некоторые из них:
- Для вычисления площади квадрата, необходимо умножить длину стороны на саму себя: S = a*a, где а – длина стороны квадрата.
- Для вычисления площади прямоугольника, необходимо умножить длину одной стороны на длину другой стороны: S = a*b, где a и b – длины сторон прямоугольника.
- Для вычисления площади треугольника, можно воспользоваться формулой Герона: S = √(p*(p-a)*(p-b)*(p-c)), где p – полупериметр треугольника, а a, b и c – длины его сторон.
Вычисление площади фигуры позволяет получить важную информацию о ее размере и форме. Это может быть полезно при проектировании, строительстве или решении геометрических задач. Необходимо выбрать правильную формулу и учесть все необходимые параметры для получения точного результата.
Используя эти простые формулы и методы, можно легко вычислить площадь различных фигур и применить полученные данные в решении конкретных задач.
Как найти сторону треугольника
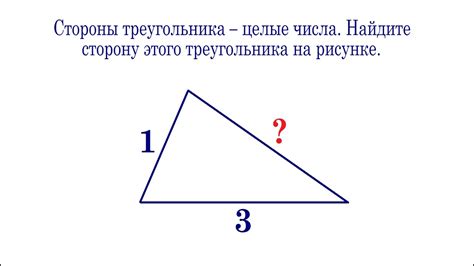
Для вычисления стороны треугольника, если известны другие стороны, можно использовать теорему Пифагора или закон синусов в зависимости от информации, которая имеется.
Если известны длины двух сторон треугольника и угол между ними, можно воспользоваться законом синусов. Формула для нахождения третьей стороны будет выглядеть следующим образом:
c = sqrt(a^2 + b^2 - 2ab*cos(C))
Где c - третья сторона треугольника, a и b - известные стороны, а C - угол между ними.
Если известны длины всех трех сторон треугольника, то для нахождения третьей стороны можно использовать теорему Пифагора. Формула будет иметь вид:
c = sqrt(a^2 + b^2)
Где c - третья сторона треугольника, a и b - известные стороны.
Теперь вы знаете, как найти сторону треугольника, используя различные математические формулы. Помните, что корректное использование данных формул требует точных измерений и углов и сторон треугольника.
Примеры вычислений

Рассмотрим несколько примеров вычисления периметра, площади и стороны различных геометрических фигур.
| Фигура | Периметр | Площадь | Известный параметр | Результат |
|---|---|---|---|---|
| Квадрат | 4 * сторона | сторона * сторона | сторона = 5 см | Периметр: 20 см Площадь: 25 см² |
| Прямоугольник | 2 * (длина + ширина) | длина * ширина | длина = 6 см, ширина = 4 см | Периметр: 20 см Площадь: 24 см² |
| Треугольник | сторона₁ + сторона₂ + сторона₃ | (основание * высота) / 2 | сторона₃ = 8 см, высота = 6 см | Периметр: 23 см Площадь: 24 см² |
| Круг | 2 * π * радиус | π * радиус² | радиус = 3 см | Периметр: 18.85 см Площадь: 28.27 см² |
Это только некоторые примеры вычислений. В каждом конкретном случае формулы могут варьироваться в зависимости от параметров, заданных для фигуры.
Полезные советы

1. Запомните основные формулы:
Для вычисления периметра и площади разных фигур существуют специальные формулы. Необходимо запомнить основные из них, чтобы в дальнейшем использовать их при решении задач. Например, для прямоугольника периметр вычисляется по формуле P = 2(a + b), где a и b - длины сторон, а площадь вычисляется по формуле S = a * b.
2. Используйте правило замены:
Если вам известны величины сторон в разных единицах измерения, и необходимо выполнить вычисления, лучше всего привести все к одной единице измерения. Например, если одна сторона прямоугольника указана в сантиметрах, а другая - в метрах, приведите все к метрам или сантиметрам, чтобы получить однородные значения.
3. Не забывайте про единицы измерения:
При вычислении площади или периметра фигур необходимо учитывать единицы измерения. Убедитесь, что единицы измерения отражены в ответе и соответствуют задаче. Например, если в задаче указано вычислить площадь прямоугольника в квадратных метрах, ответ тоже должен быть в квадратных метрах.
4. Проверяйте свои расчеты:
После выполнения вычислений не забудьте дважды проверить их. Ошибки могут привести к неверному результату, поэтому выделите время на проверку своих расчетов. Убедитесь, что вы правильно вычислили все стороны, применили правильные формулы и провели все необходимые операции.
5. Практикуйтесь в решении задач:
Чем больше вы будете практиковаться в решении задач по вычислению периметра, площади и сторон фигур, тем лучше вы разберетесь в этой теме. Решайте задачи разной сложности, изучайте новые методы вычислений и совершенствуйте свои навыки. В конечном итоге, практика приведет к совершенству!