Процентные задачи – одна из важных частей программы по математике для учеников 6 класса. Они позволяют развить навыки решения задач, а также оттачивают логическое мышление учащихся. Задачи с процентами – это не только математические расчеты, но и практическое применение этих расчетов в реальной жизни.
Чтобы успешно решать задачи с процентами, важно знать основные понятия и формулы: процент, основа, наценка, скидка и другие. Необходимо также понять, что процент – это доля от числа, она обозначает количество сотых долей от этого числа. Аргументированное решение задач, связанных с процентами, требует уверенности и ясного понимания этих понятий.
В настоящей статье мы рассмотрим несколько типовых задач с процентами, которые могут встретиться ученикам 6 класса. Мы разберем основные шаги решения задач и дадим полезные советы, которые помогут разобраться с разными вариантами формулировки заданий. Главное – не бояться ошибиться и тренироваться решать задачи на проценты, потому что практика – это ключ к успеху в изучении этого раздела математики.
Понятие процента и его применение
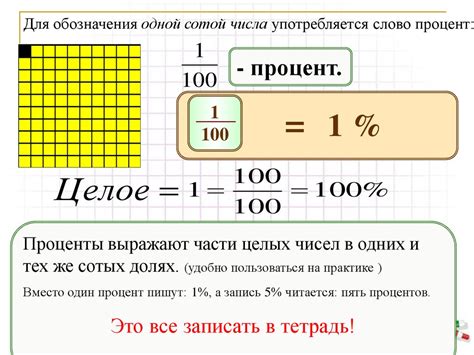
Проценты находят широкое применение в различных областях. В математике они позволяют решать задачи на нахождение процентных значений, процентных изменений, скидок, наценок и других величин.
Задачи с процентами могут быть различными. Например, для решения задачи на нахождение процентного значения нужно умножить число на процент и разделить результат на 100.
Чтобы решать задачи с процентами, необходимо знать основные формулы:
1. Процент от числа: процент = (число * процент) / 100
2. Отношение процента к числу: число = (процент * 100) / процент
3. Процентный прирост: прирост = (начальное значение * процент) / 100
Нужно помнить, что проценты могут выражаться как десятичные дроби. Например, 25% в десятичном виде будет равно 0,25.
Чтобы успешно решать задачи с процентами, необходимо разбираться в условиях задачи, применять соответствующую формулу и правильно выполнять вычисления.
Проценты – важный инструмент, используемый в жизни для решения финансовых, экономических и других задач. Изучение процентов позволяет развивать навыки анализа данных и принятия решений на основе математических расчетов.
Процент, десятичная дробь и обыкновенная дробь
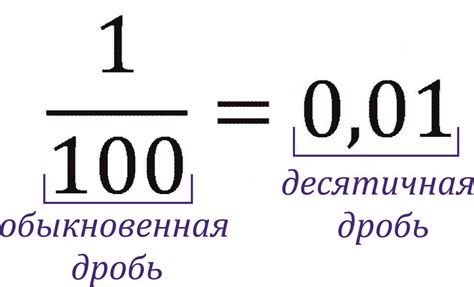
Чтобы выразить процент как десятичную дробь, необходимо делить число процентов на 100. Например, 50% = 50/100 = 0,5.
Чтобы выразить процент как обыкновенную дробь, необходимо записать число процентов в числителе и 100 в знаменателе. Например, 50% = 50/100 = 1/2.
Часто проценты используются для решения задач в математике. Например, если нужно найти 20% от числа, можно записать это как десятичную дробь (20/100 = 0,2) или как обыкновенную дробь (20/100 = 1/5). Затем надо умножить это число на изначальное число, чтобы получить результат.
Понимание процентов, десятичных дробей и обыкновенных дробей поможет решать задачи с процентами и легче разобраться в математике для 6 класса.
Проценты как способ измерить сравнительные изменения

Проценты позволяют нам легко выражать доли и изменения величин. Например, если мы хотим узнать, какой процент от всего класса составляют девочки, мы можем просто разделить количество девочек на общее количество учеников и умножить результат на 100.
Проценты также позволяют нам измерять изменения со временем или сравнивать различные значения. Мы можем выразить процентное изменение относительно исходного значения или сравнить два разных значения, используя процентные выражения.
Проценты и доли

Процент обозначается символом "%". Он равен количеству сотых частей. Например, 25% представляет собой 25 из 100 частей или 1/4.
Для решения задач, связанных с процентами, важно уметь работать с долями и пропорциями. Например, если нужно найти процент от числа, можно использовать следующую формулу:
Процент = (Доля/100) * Число
Для нахождения доли от числа можно использовать формулу:
Доля = (Процент * Число) / 100
Проценты и доли могут быть полезными при вычислении скидок или наценок, при расчете популяции или статистики и во многих других ситуациях.
Важно помнить, что проценты не всегда обозначаются числами, они также могут быть представлены в виде дробей или десятичных дробей. Например, 50% эквивалентно 1/2 или 0,5.
Понимание процентов и долей поможет ученикам расширить свои математические навыки и применять их в повседневной жизни. Умение решать задачи с процентами позволит им быть лучше подготовленными к финансовым решениям и анализу данных.
Процент как множитель и коэффициент пропорциональности
Процент можно рассматривать как множитель или коэффициент пропорциональности. Во-первых, процентные значения можно выразить в виде десятичной дроби или десятичного числа от 0 до 1. Например, 50 процентов можно записать как 0,5 или 1/2. Во-вторых, проценты могут использоваться для выражения пропорциональных отношений между двумя значениями.
| Процент | Множитель | Пропорциональность |
|---|---|---|
| 25% | 0,25 | 1:4 |
| 50% | 0,5 | 1:2 |
| 75% | 0,75 | 3:4 |
| 100% | 1 | 1:1 |
Чтобы решить задачу с процентами, нужно уметь применять соответствующую формулу или правило пропорциональности. Например, при решении задач на нахождение процента от числа нужно умножить число на соответствующий множитель (процент в виде десятичной дроби) или использовать пропорцию. А при решении задач на изменение числа на процент нужно умножить число на соответствующий коэффициент пропорциональности (процент в виде десятичного числа).
Использование процента как множителя или коэффициента пропорциональности позволяет упростить вычисления и решить задачи с процентами в математике для 6 класса. Знание основных формул и правил пропорциональности поможет ученикам справиться с задачами на эту тему и применять их в реальной жизни для решения практических задач связанных с процентами.
Расчет процента от числа
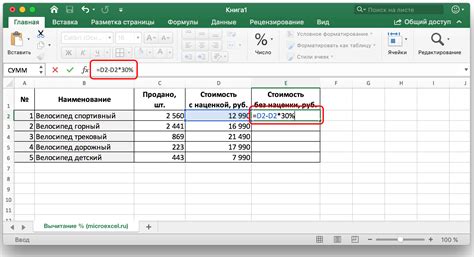
Для расчета процента от числа важно знать два значения: процент и число, от которого требуется найти процентную часть.
Для решения этой задачи можно использовать формулу:
Часть = (Число * Процент) / 100
Для начала нужно умножить число на процент, а затем результат разделить на 100.
Например, если мы хотим найти 30 процентов от числа 200, то по формуле получаем:
Часть = (200 * 30) / 100 = 60
Таким образом, 30 процентов от числа 200 равны 60.
Этот метод применим для расчета любого процента от числа. Если известно число и процент, то можно легко найти часть от числа.
Расчет числа при заданном проценте

При решении задач с процентами важно уметь вычислять число при заданном проценте. Для этого мы используем формулу:
Число = (Процент * Исходное число) / 100
Где:
- Число - искомое число, которое нужно найти;
- Процент - заданный процент от исходного числа;
- Исходное число - число, от которого нужно найти процент.
Давайте рассмотрим пример для лучшего понимания. Предположим, что в магазине проходит акция, и товар снизился на 20%. Чтобы найти новую цену товара, мы применяем формулу:
Цена товара со скидкой = (20 * Исходная цена товара) / 100
Если исходная цена товара была, например, 1000 рублей, то новая цена товара со скидкой будет:
Цена товара со скидкой = (20 * 1000) / 100 = 200 рублей
Таким образом, новая цена товара со скидкой составит 200 рублей.
Как видно из примера, чтобы найти число при заданном проценте, мы умножаем процент на исходное число и делим на 100. Результатом будет искомое число.
Эта формула поможет вам решать задачи с процентами, когда необходимо найти число при заданном проценте. Теперь вы можете использовать ее для самостоятельного решения подобных задач.
Нахождение процента от числа

Для решения задач с процентами в математике нужно уметь находить процент от числа. Это очень полезное умение, потому что позволяет решать множество задач в повседневной жизни.
Если нам нужно найти процент от числа, то мы можем воспользоваться следующей формулой:
Процент от числа = (Число * Процент) / 100
Например, если нам нужно найти 20% от числа 80, мы можем воспользоваться этой формулой:
| Число | Процент | Процент от числа |
|---|---|---|
| 80 | 20 | (80 * 20) / 100 = 16 |
Таким образом, 20% от числа 80 равно 16.
Зная эту формулу, вы сможете легко решать задачи, связанные с нахождением процентов от чисел. Это может быть полезно, например, при расчете скидки на товары или при расчете налогов.
Приложения процентов в повседневной жизни

Одним из наиболее распространенных применений процентов является вычисление скидок в магазинах. Например, если товар имеет скидку 20%, то мы можем легко рассчитать его стоимость после скидки. Применение процентов также позволяет нам сравнивать разные скидки и выбирать наиболее выгодную.
В области финансов проценты имеют огромное значение. Например, при рассмотрении кредита или ипотеки нам необходимо учитывать процентные ставки и вычислять сумму выплаты по месяцам или годам. Знание процентов также полезно при выборе депозита в банке, так как мы можем оценить, какая сумма будет накапливаться с процентами за определенный период времени.
Кроме того, проценты имеют значение при расчете налогов. Например, при расчете НДФЛ мы учитываем определенный процент с дохода и рассчитываем сумму налога. Знание процентов также полезно при расчете займов, погашении кредитов и определении процентных ставок по ним.
В повседневной жизни мы часто сталкиваемся с ситуациями, где знание процентов помогает нам принимать осознанные решения. Будь то сравнение цен на товары, выбор наиболее выгодной скидки или расчет финансовых вопросов, умение работать с процентами является необходимым навыком для любого человека.
| Применение процентов в повседневной жизни |
|---|
| - Расчет скидок в магазинах |
| - Оценка процентных ставок по кредитам и депозитам |
| - Расчет налогов |
| - Расчет займов и погашение кредитов |
Задачи с процентами на время и расстояние

Задачи с процентами на время и расстояние помогают решать практические задачи, связанные с путешествиями и временем. Они позволяют научиться работать с процентами и применять их в реальных ситуациях.
Приведем пример задачи:
| Условие задачи | Решение |
|---|---|
| Маша прошла первые 20 километров бегом со средней скоростью 10 км/ч, а оставшиеся 40 километров - на велосипеде со средней скоростью 20 км/ч. Сколько времени Маша потратила на всё путешествие? | Чтобы найти общее время, нужно посчитать время, которое Маша потратила на бег и на велосипед. Время на бег = расстояние / скорость = 20 км / 10 км/ч = 2 часа. Время на велосипед = расстояние / скорость = 40 км / 20 км/ч = 2 часа. Общее время = время на бег + время на велосипед = 2 часа + 2 часа = 4 часа. |
Таким образом, Маша потратила 4 часа на всё путешествие.
Применяя знания о процентах и простых долях, ученики смогут успешно решать подобные задачи на время и расстояние, а также применять полученные навыки в повседневной жизни.