Понимание площади фигур является важным элементом математического образования учеников начальной школы. Во время изучения геометрии, ученикам будет предложено найти площадь различных фигур, включая треугольники. Для учеников 4 класса, понимание, как найти площадь треугольника на клетчатой бумаге, может быть задачей, вызывающей затруднения.
В этой статье мы рассмотрим простой метод нахождения площади треугольника на клетчатой бумаге, который поможет ученикам лучше понять эту концепцию. Метод основан на том, что ученику нужно разделить треугольник на прямоугольники и посчитать площадь каждого прямоугольника.
Для начала, ученик должен нарисовать треугольник на клетчатой бумаге. Затем, необходимо провести горизонтальные или вертикальные линии через каждую клетку внутри треугольника. После этого, ученик будет видеть, как треугольник разбивается на множество прямоугольников, каждый из которых имеет одну сторону равной длине одной клетки, а другую - длину одной или нескольких клеток.
Суть и применение площади треугольника
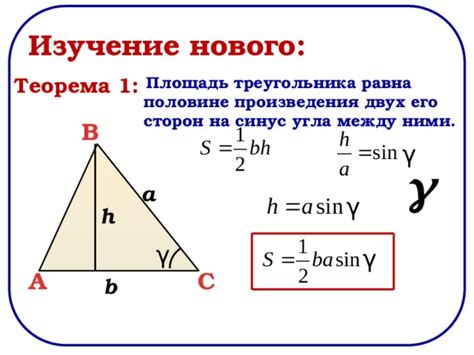
Площадь треугольника может иметь множество применений. В архитектуре, инженерии и строительстве, знание площади треугольника необходимо при проектировании и вычислении площадей фундаментов, крыш, полов и других элементов конструкций.
В ежедневной жизни площадь треугольника может быть полезной, например, при покупке ковра или обоев для комнаты, где нужно узнать площадь пола, чтобы выбрать нужное количество материала.
Так же, вычисление площади треугольника помогает развивать логическое мышление, аналитические и пространственные навыки учащихся. Последовательность действий, необходимая для нахождения площади, помогает развить навыки работать с числами, использовать формулу для нахождения ответа и применять их в решении различных задач.
Важно понимать, что площадь треугольника может быть вычислена разными способами, в зависимости от предоставленных данных. Простые методы, такие как разделение треугольника на два прямоугольника или использование формулы для расчета площади по длинам сторон и высоте, могут быть использованы для решения задач на уровне четвертого класса.
| Метод | Формула | Применение |
|---|---|---|
| Разделение на прямоугольники | Площадь = (a * h) / 2 | Простой метод для треугольников, у которых есть высота |
| По длинам сторон и высоте | Площадь = (a * h) / 2 | Применяется при известных значениях длин сторон и высоты |
Использование площади треугольника в решении задач развивает универсальные математические компетенции и способствует формированию логического мышления, необходимых не только в школе, но и в повседневной жизни.
Как измерить стороны треугольника
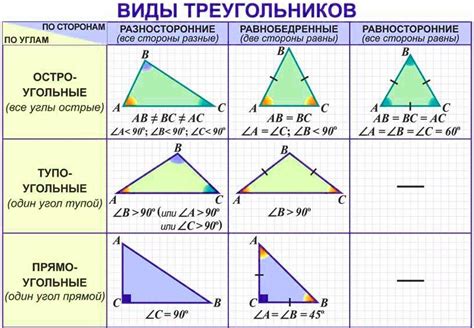
Для измерения сторон треугольника на клетчатой бумаге, понадобятся линейка и карандаш. Вот несколько шагов, которые помогут вам измерить стороны треугольника с точностью:
- Выберите одну сторону треугольника и пометьте ее начало точкой A. От этой точки с помощью линейки проведите линию вдоль стороны треугольника, чтобы указать ее направление.
- Установите ноль линейки в начале отрезка и переместите линейку вдоль стороны треугольника, чтобы измерить длину этой стороны. Отметьте конец стороны точкой B.
- Повторите шаги 1-2 для измерения двух других сторон треугольника, помечая их концы точками C и D соответственно.
Теперь у вас есть все три точки треугольника - A, B и C. Вы можете измерить каждую сторону треугольника, измеряя расстояние между соответствующими точками.
Важно помнить, что измерения должны быть точными. При измерении следует быть внимательным и аккуратным, чтобы получить правильные значения сторон треугольника.
Способы нахождения площади треугольника
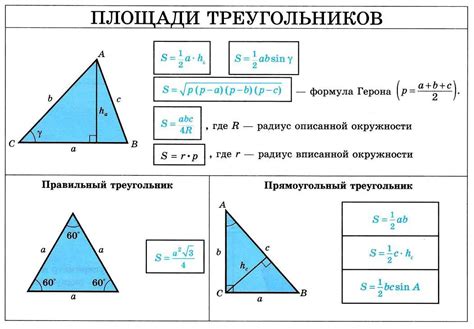
Существует несколько способов нахождения площади треугольника:
1. Формула Герона: если известны длины всех сторон треугольника, можно воспользоваться формулой Герона, которая задается следующим образом:
S = √(p * (p - a) * (p - b) * (p - c)),
где S - площадь треугольника, a, b, c - длины сторон, а p - полупериметр треугольника (p = (a + b + c) / 2).
2. Площадь по высоте: если известны длины основания и высоты треугольника, можно найти площадь с помощью следующей формулы:
S = (a * h) / 2,
где S - площадь треугольника, a - длина основания, h - высота треугольника.
3. Площадь по координатам: если известны координаты вершин треугольника на плоскости, можно воспользоваться формулой площади по координатам, которая задается следующим образом:
S = (|x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|) / 2,
где S - площадь треугольника, (x1, y1), (x2, y2), (x3, y3) - координаты вершин треугольника.
Эти способы помогут ученикам 4 класса легко находить площадь треугольника на клетчатой бумаге, используя доступные им знания и навыки.
Метод половинного произведения сторон

Для применения этого метода, нужно знать длины всех трех сторон треугольника. Первым шагом необходимо разделить все стороны на 2. Затем нужно найти половину произведения длин всех сторон треугольника. После этого можно найти высоту треугольника, проведя перпендикуляр от места, где сходятся две стороны, до третьей стороны. Далее нужно найти площадь треугольника, умножив получившуюся высоту на половину произведения сторон.
Применение метода половинного произведения сторон позволяет быстро и удобно вычислять площадь треугольника на клетчатой бумаге, не прибегая к сложным формулам и вычислениям. Этот метод особенно полезен для учеников 4 класса, которые только начинают изучение геометрии и могут использовать его для решения задач на построение и вычисление площади треугольников.
Метод треугольника с основанием на оси абсцисс
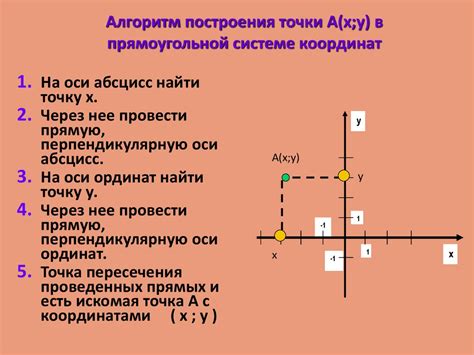
Для использования этого метода необходимо:
- Найти координаты вершин треугольника на клетчатой бумаге.
- Провести вертикальную прямую из вершины треугольника, лежащей на оси абсцисс, до основания треугольника.
- Подсчитать количество клеток, которые находятся под этой прямой.
Количество клеток, находящихся под прямой, будет являться площадью треугольника.
Пример:
- Вершины треугольника имеют координаты (1, 3), (4, 1) и (7, 3).
- Одно из оснований лежит на оси абсцисс и имеет координату (4, 1).
- Проведем вертикальную прямую из вершины (4, 1) до основания треугольника.
- Посчитаем количество клеток, находящихся под этой прямой.
- Получим площадь треугольника по найденному количеству клеток.
Используя метод треугольника с основанием на оси абсцисс, ученики 4 класса могут легко и понятно вычислить площадь треугольника на клетчатой бумаге.
Метод треугольника с основанием на оси ординат
Для вычисления площади треугольника по данному методу необходимо знать длину его основания (высоту) и ширину основания (количество клеток на оси ординат).
Процесс вычисления площади треугольника по данному методу можно разделить на следующие шаги:
- Запишите длину основания (высоту) треугольника.
- Запишите ширину основания (количество клеток на оси ординат).
- Вычислите площадь прямоугольника, образованного основанием и высотой треугольника.
- Вычтите площадь треугольника, образованного высотой треугольника и площадью прямоугольника из шага 3.
- Полученный результат – площадь треугольника на клетчатой бумаге.
Теперь вы знаете метод треугольника с основанием на оси ординат и можете использовать его для вычисления площади треугольника на клетчатой бумаге в вашей задаче.
Метод треугольника с вершиной в начале координат
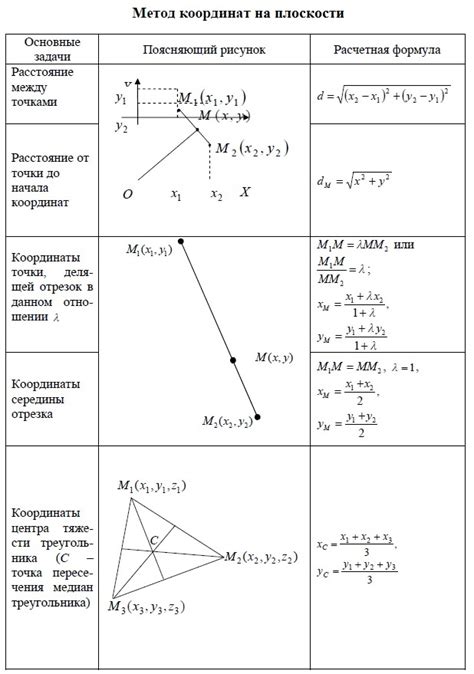
Для использования этого метода требуется следующая последовательность действий:
- Нарисуйте треугольник на клетчатой бумаге с вершиной в начале координат.
- Разбейте треугольник на прямоугольники и квадраты, используя горизонтальные и вертикальные линии сетки.
- Посчитайте площадь каждого прямоугольника или квадрата, поместив их внутрь треугольника.
- Сложите все площади прямоугольников и квадратов, чтобы получить площадь треугольника.
Важно отметить, что при разбиении треугольника на фигуры необходимо принимать во внимание только те прямоугольники и квадраты, которые полностью помещаются внутри треугольника.
Применение метода треугольника с вершиной в начале координат позволяет ученикам 4 класса легко вычислить площадь треугольника без использования сложных формул или математических операций. Этот метод развивает абстрактное мышление, логику и пространственное воображение учеников.
Объединение методов для нахождения площади
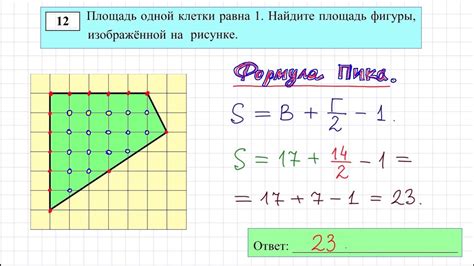
Для определения площади треугольника, можно использовать различные методы. В данной статье мы рассмотрим два из них: метод подсчета количества клеток на клетчатой бумаге и метод использования формулы площади треугольника.
- Метод подсчета клеток на клетчатой бумаге:
- Расположите треугольник на клетчатой бумаге так, чтобы одна из его сторон лежала поперек клеток.
- Подсчитайте количество полностью закрашенных клеток внутри треугольника.
- Если треугольник имеет незакрашенные клетки, отнимите количество таких клеток от общего количества закрашенных клеток.
- Площадь треугольника равна количеству закрашенных клеток.
- Измерьте длину основания треугольника и высоту, опущенную на это основание.
- Умножьте полученные значения длины основания и высоты.
- Разделите полученное значение на 2.
- Площадь треугольника равна полученному значению.
Оба метода позволяют найти площадь треугольника на клетчатой бумаге. Выбор метода зависит от предпочтений ученика и доступности необходимых инструментов. Важно помнить, что правильное выполнение всех шагов обеспечит точность результата.