Диаметр и радиус - ключевые понятия в геометрии, которые часто используются для описания размеров и форм объектов. Радиус - это половина диаметра окружности, а диаметр - самая длинная линия, проходящая через центр окружности и соединяющая две противоположные точки на ее окружности. Понимание взаимосвязи между радиусом и диаметром крайне важно при решении задач, связанных с геометрией и конструкцией различных объектов.
Но как найти диаметр через радиус без лишних сложностей? Существует простая математическая формула, которую можно использовать для расчета диаметра.
Диаметр можно выразить через радиус, используя следующую формулу:
d = 2r
Где d - диаметр, r - радиус.
Для примера, рассмотрим окружность, радиус которой равен 5 сантиметрам. Чтобы найти ее диаметр, просто умножьте значение радиуса на 2:
d = 2 * r = 2 * 5 = 10 сантиметров
Таким образом, диаметр окружности с радиусом 5 сантиметров равен 10 сантиметрам.
Простой способ нахождения диаметра через радиус
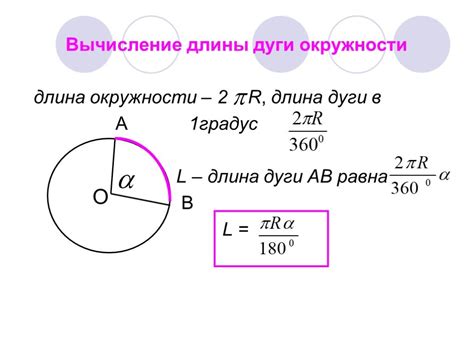
Для нахождения диаметра через радиус достаточно удвоить значение радиуса. То есть, диаметр (D) можно вычислить по следующей формуле:
D = 2 * r
где D - диаметр, r - радиус.
Данный способ нахождения диаметра через радиус очень прост и не требует дополнительных вычислений.
Пример:
Пусть задан радиус окружности r = 4 см. Для нахождения диаметра применяем формулу:
D = 2 * 4 = 8 см
Таким образом, диаметр окружности будет равен 8 см.
Пользуясь данной простой формулой, вы сможете быстро и легко вычислить диаметр окружности по заданному радиусу. Это может быть полезно в различных ситуациях, например, при решении геометрических задач или при проектировании объектов с использованием окружностей.
Формула расчета диаметра по радиусу
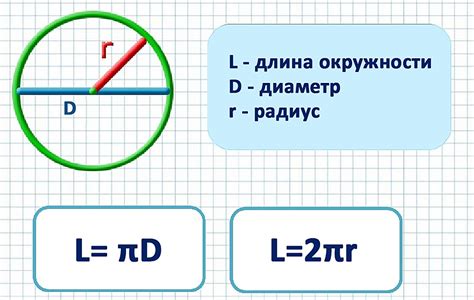
Формула для вычисления диаметра по радиусу задается выражением:
d = 2r
где d - диаметр, а r - радиус окружности.
Другими словами, чтобы найти диаметр, нужно умножить радиус на два.
Например, если радиус окружности составляет 5 см, то диаметр будет равен:
| Радиус (см) | Диаметр (см) |
|---|---|
| 5 | 10 |
Таким образом, диаметр окружности будет составлять 10 см.
Примеры расчета

Для лучшего понимания использования формулы для расчета диаметра через радиус, рассмотрим несколько примеров:
Пример 1:
Имеется окружность с радиусом 5 см. Для определения диаметра используем формулу:
Диаметр = 2 × радиус
Подставляем значение радиуса: Диаметр = 2 × 5 см = 10 см.
Таким образом, диаметр этой окружности равен 10 см.
Пример 2:
Предположим, что у нас есть окружность с радиусом 3 м. Для вычисления диаметра, применим формулу:
Диаметр = 2 × радиус
Подставляем значение радиуса: Диаметр = 2 × 3 м = 6 м.
Таким образом, диаметр этой окружности равен 6 м.
Пример 3:
Пусть у нас есть окружность с радиусом 2.5 дм. Для определения диаметра используем формулу:
Диаметр = 2 × радиус
Подставляем значение радиуса: Диаметр = 2 × 2.5 дм = 5 дм.
Таким образом, диаметр этой окружности равен 5 дм.
Используя указанные примеры, можно увидеть, как просто и быстро можно вычислить диаметр окружности, зная ее радиус.
Зачем нужно знать диаметр по радиусу?

Вот несколько примеров ситуаций, где знание диаметра по радиусу может быть полезным:
- Инженеры и архитекторы могут использовать простую формулу для вычисления диаметра, чтобы правильно разместить и распределить элементы конструкции, такие как колонны, стойки или провода.
- Техники и механики могут использовать диаметр для определения подходящего размера инструментов или запасных частей.
- При изготовлении или сборке предметов, знание диаметра может помочь точно измерить и разместить отверстия, винты или гайки, чтобы они соответствовали заданным параметрам.
- Математики и физики могут использовать диаметр при решении задач, связанных с окружностями и геометрией. Знание диаметра позволяет вычислять площадь, периметр и другие параметры фигур.
- В медицине, диаметр может быть важным параметром для измерения или оценки размера различных структур в организме пациента на рентгеновских снимках или других изображениях.
В общем, зная диаметр по радиусу, мы можем получить дополнительные данные о форме и размере объекта или структуры, что помогает в решении различных задач и принятии важных решений.
Практическое применение формулы нахождения диаметра через радиус
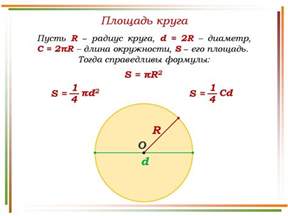
Примеры практического применения:
- Строительство: при проектировании зданий и сооружений необходимо учитывать размеры и пропорции. Например, если известен радиус колонны или столба, можно посчитать диаметр, чтобы правильно подобрать материал для опоры.
- Машиностроение: при разработке механизмов и машин важно знать размеры деталей. Зная радиус шестерни или вала, можно вычислить диаметр, что поможет выбрать подходящий инструмент для обработки или правильно спроектировать соединение.
- Техника и электроника: при разработке и монтаже различных устройств, часто требуется знать размеры компонентов. Например, если известно значение радиуса электронной пайки, можно рассчитать диаметр пайки, чтобы выбрать правильную насадку на паяльник.
- Геометрия: формула для нахождения диаметра через радиус является одной из основных в геометрии. Используя эту формулу, можно решать различные задачи, связанные с окружностями и кругами, например, находить диаметр для расчета площади или периметра.
Использование формулы для нахождения диаметра через радиус позволяет выполнять простые и быстрые расчеты, что особенно полезно в ситуациях, когда точные размеры объекта или структуры неизвестны, но имеется информация о радиусе. Открытие и применение этой формулы позволяет экономить время и ресурсы при проектировании, строительстве и производстве различных изделий и конструкций.
Полезные советы по использованию формулы нахождения диаметра по радиусу
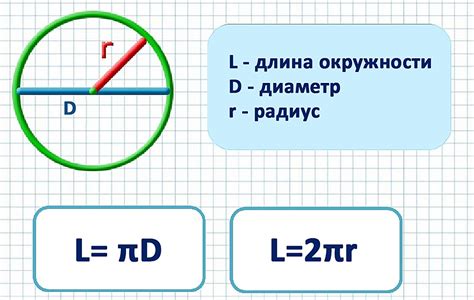
Теперь рассмотрим несколько полезных советов по использованию данной формулы:
- Вводите значения радиуса с нужной точностью. Если вы работаете с дробными числами, то старательно округляйте результаты расчетов.
- Используйте единицы измерения, соответствующие ситуации. Например, если вы работаете с длинами в сантиметрах, то и радиус и диаметр следует вычислять в сантиметрах.
- Проверяйте результаты, особенно при использовании готовых формул. Математика может быть непредсказуемой, поэтому всегда старайтесь проверять ваши расчеты, чтобы избежать ошибок.
- Не забывайте о приоритетности операций. В формуле d = 2r, сначала нужно умножить радиус на 2, а затем присвоить полученное значение диаметру.
- Применяйте данную формулу для нахождения диаметра в различных ситуациях. Например, вы можете использовать ее при расчете диаметра цилиндров, шаров, колес автомобиля и многих других предметов, которые имеют форму окружности.
Использование формулы нахождения диаметра по радиусу может быть очень полезным при решении различных задач. Надеемся, что наши советы помогут вам использовать эту формулу правильно и эффективно. Удачи в ваших расчетах!