Радиус цилиндра - один из основных параметров, определяющих его форму и размеры. Вычисление радиуса цилиндра может быть полезным при проектировании и строительстве, а также при решении различных задач в физике и математике. В данной статье мы рассмотрим простой и эффективный способ вычисления радиуса цилиндра.
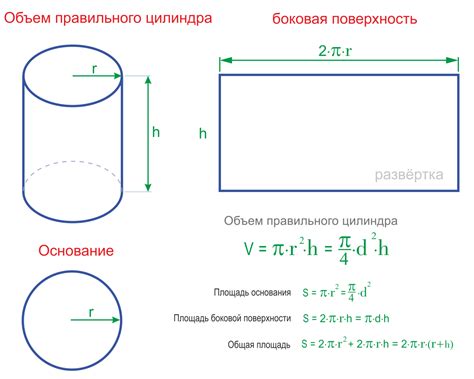
Для вычисления радиуса цилиндра необходимо знать его объем и высоту. Объем цилиндра можно вычислить по формуле V = π * R^2 * H, где V - объем, R - радиус основания цилиндра, H - высота цилиндра. Из этой формулы мы можем выразить радиус цилиндра следующим образом: R = sqrt(V / (π * H)). Таким образом, нам необходимо знать объем и высоту цилиндра для вычисления его радиуса.
Для определения объема цилиндра необходимо знать его высоту и площадь основания. Площадь основания цилиндра можно вычислить по формуле S = π * R^2, где S - площадь, R - радиус основания цилиндра. Из этой формулы мы можем выразить радиус цилиндра следующим образом: R = sqrt(S / π). Таким образом, нам необходимо знать площадь основания цилиндра и его высоту для вычисления радиуса.
Как определить радиус цилиндра шаг за шагом?
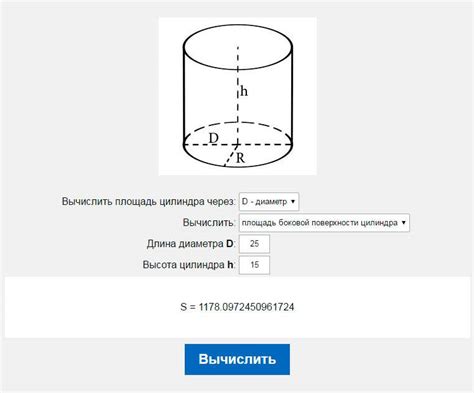
Шаг 1: Измерьте диаметр цилиндра.
Примечание: диаметр - это расстояние между двумя точками на противоположных сторонах цилиндра через его центр.
Шаг 2: Разделите диаметр на 2, чтобы получить радиус.
Примечание: радиус цилиндра - это расстояние от центра до любой точки на его боковой поверхности.
Шаг 3: Запишите полученное значение радиуса.
Таким образом, следуя этим шагам, вы можете определить радиус цилиндра шаг за шагом и использовать его для решения различных задач, связанных с цилиндром.
Измерение высоты и объема цилиндра

Для вычисления радиуса цилиндра, важно уметь правильно измерять его высоту и объем. В этом разделе мы рассмотрим основные методы измерения высоты и объема цилиндра.
Высота цилиндра – это расстояние между его двумя плоскими основаниями. Для определения высоты можно использовать рулетку или линейку. Поместите основание цилиндра на плоскую поверхность и аккуратно измерьте расстояние до верхней плоскости.
Чтобы вычислить объем цилиндра, нужно знать его высоту и радиус основания. Объем цилиндра вычисляется по формуле: V = πr²h, где V – объем, r – радиус, h – высота. Радиус основания цилиндра можно найти, используя измеренные значения.
Измерение высоты и объема цилиндра является одной из ключевых задач в геометрии. Правильное измерение поможет вам точно вычислить радиус и другие параметры цилиндра, что будет полезно при решении различных задач и заданий.
Вычисление площади основания цилиндра
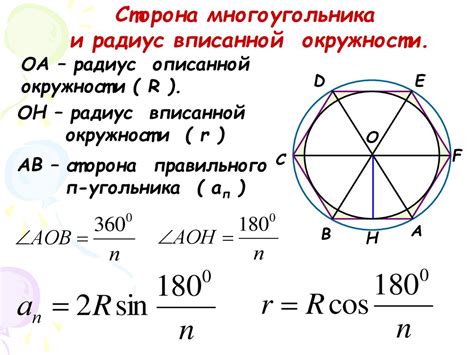
Для вычисления площади основания цилиндра необходимо знать его форму. Основание цилиндра может быть кругом или многоугольником, но в большинстве случаев используется круглое основание.
Формула для вычисления площади круга: Sосн = π * r², где Sосн - площадь основания цилиндра, а r - радиус основания.
Для использования этой формулы необходимо знать радиус, то есть расстояние от центра круга до его края. Радиус можно вычислить, зная диаметр или окружность круга.
Формула для вычисления радиуса по диаметру: r = d / 2, где r - радиус, а d - диаметр.
Формула для вычисления радиуса по окружности: r = C / (2 * π), где r - радиус, а C - окружность.
Зная радиус основания цилиндра, можно легко вычислить площадь основания, используя формулу Sосн = π * r².
Использование формулы для вычисления радиуса
Для вычисления радиуса цилиндра существует простая формула, которая позволяет рассчитать его значение на основе других известных параметров. Для этого необходимо знать высоту и объем цилиндра.
Формула для вычисления радиуса цилиндра:
r = √(V / (πh))
где r - радиус цилиндра, V - объем цилиндра, h - высота цилиндра, π - постоянное значение числа пи, равное примерно 3.14159.
Для использования формулы необходимо знать значения объема и высоты цилиндра, которые можно измерить или получить из других источников. Подставив известные значения в формулу, можно вычислить радиус цилиндра.
Например, если известны значения объема V=100 см³ и высоты h=10 см, то радиус цилиндра можно вычислить следующим образом:
r = √(100 / (π*10)) ≈ √(10 / 3.14159) ≈ √(31.83397) ≈ 5.64599
Таким образом, радиус цилиндра с объемом 100 см³ и высотой 10 см составляет примерно 5.64599 см.
Использование формулы позволяет просто и эффективно вычислять радиус цилиндра, используя известные параметры. Это особенно полезно для решения задач и практических применений, связанных с цилиндрами.
Практическое использование полученного значения радиуса

Важно отметить, что значение радиуса может быть использовано не только в математических вычислениях, но и в реальной жизни. Например, зная радиус цилиндра, мы можем определить, какой диаметр трубы необходим для подключения канализации или водопровода. Также значение радиуса может быть использовано при проектировании инженерных систем, строительстве и архитектуре.
Кроме того, зная радиус цилиндра, мы можем также определить его форму и структуру, что может быть полезно при проектировании и моделировании различных объектов. Радиус цилиндра может быть использован для создания трехмерной модели, изготовления прототипа или даже печати объекта на 3D-принтере.
Таким образом, практическое использование полученного значения радиуса цилиндра не ограничивается только математическими вычислениями, но распространяется на различные сферы нашей жизни. Знание радиуса цилиндра может быть полезным инструментом для решения задач и создания новых проектов.