При изучении геометрии седьмого класса одной из важных задач является построение вписанной окружности в треугольник. Вписанная окружность – это окружность, которая касается каждой стороны треугольника.

Построение вписанной окружности в треугольник возможно с использованием только циркуля и линейки. Для этого необходимо выполнить несколько шагов. Сначала нарисуем треугольник, затем построим биссектрисы каждого из углов, которые пересекутся в точке. Далее, с помощью циркуля проведем окружность с центром в этой точке и радиусом, равным расстоянию от центра окружности до любой стороны треугольника.

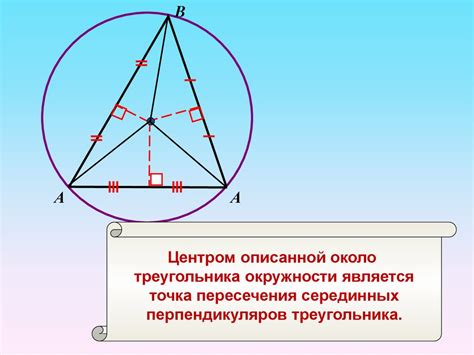
Вписанная окружность обладает рядом интересных свойств. Например, радиус этой окружности является равным отрезком, опущенным из вершины треугольника к любой из сторон. Также, если в треугольнике построить перпендикуляр к одной из его сторон, то этот перпендикуляр будет проходить через центр вписанной окружности.

Построение вписанной окружности в треугольник - это важный шаг на пути к изучению геометрии и решению различных задач с помощью циркуля и линейки. Знание этой техники позволяет не только строить геометрические фигуры, но и решать сложные задачи, связанные с треугольниками. Необходимые навыки и умения при построении вписанной окружности разовьются с практикой и усидчивым тренировочным процессом. Данная техника широко используется в различных областях, включая архитектуру, строительство, инженерное дело и другие. Поэтому она является неотъемлемой частью математического образования.

Построение вписанной окружности в треугольник седьмого класса

Для построения вписанной окружности в треугольник седьмого класса можно использовать следующий алгоритм:

1. Найдите середины сторон треугольника. Для этого можно использовать перпендикулярные биссектрисы, проходящие через середины сторон.
2. Проведите две перпендикулярные линии к найденным серединам сторон. Полученные точки пересечения будут являться центром и радиусом вписанной окружности.
3. Постройте окружность с найденным центром и радиусом.

Построение вписанной окружности позволяет решать различные задачи, связанные с треугольником, например, нахождение площади треугольника, нахождение длин сторон треугольника и его углов.

Построение вписанной окружности в треугольник является важным и интересным элементом геометрии. Этот навык будет полезен не только в школе, но и в дальнейшей жизни при решении различных задач и построении геометрических фигур.

Принцип вписанной окружности и ее свойства

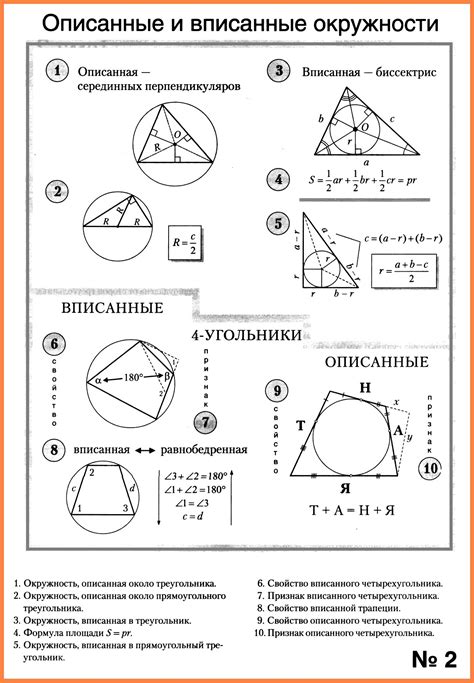
Свойства вписанной окружности:

1. Центр вписанной окружности лежит на пересечении биссектрис треугольника.
2. Расстояние от центра вписанной окружности до любой из сторон треугольника равно радиусу окружности.
3. Углы, опирающиеся на одну и ту же дугу вписанной окружности, равны.
4. Сумма углов треугольника, стоящих напротив хорды, равна 180 градусов.

Вписанная окружность имеет множество применений в геометрии и ее свойства часто используются для решения задач на построение и вычисление параметров треугольников. Поэтому понимание принципа вписанной окружности и ее свойств является важным элементом математического образования.

Инструменты и материалы для построения

Для построения вписанной окружности в треугольник вам понадобятся следующие инструменты:

1. Линейка - для измерения и построения прямых отрезков.
2. Циркуль - для построения окружности с заданным радиусом.
3. Геометрический треугольник - для проведения перпендикулярных линий и маркировки углов.
4. Карандаш и резинка - для отметок и коррекции ошибок.
5. Компас - для построения окружности с заданным центром.

Обратите внимание, что для точного построения вам также понадобится ровная и чистая поверхность, на которой вы будете работать. Убедитесь, что ваш стол или лист бумаги достаточно прочны и гладки, чтобы обеспечить точность вашего построения.

Шаги построения вписанной окружности

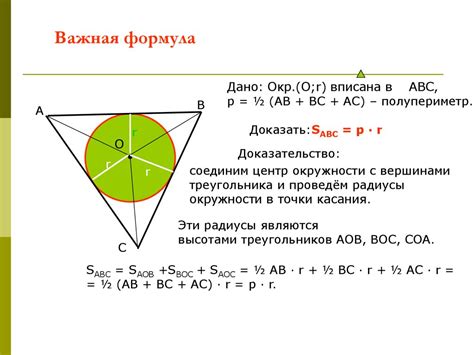
1. Возьмите рисунок треугольника и отметьте на нем середины всех сторон. Обозначьте их буквами A, B и C.
2. Соедините точки A, B и C линиями, чтобы получить медианы треугольника. Медианы - это линии, которые проходят через вершины треугольника и пересекаются в единой точке, называемой центром медиан.
3. Найдите точку пересечения медиан и обозначьте ее буквой O. Она будет являться центром вписанной окружности.
4. Измерьте расстояние от точки О до любой вершины треугольника и разделите его пополам. Обозначьте полученное расстояние буквой r.
5. Сделайте с произвольным радиусом, равным r, точку O центром и нарисуйте окружность вокруг нее.
6. Проверьте, что окружность проходит через середины всех сторон треугольника.
7. Закрашивайте треугольник и окружность, чтобы завершить построение.

Теперь вы знаете, как построить вписанную окружность в треугольник. Удачного вам рисования!

Примеры заданий на построение вписанной окружности

Для того чтобы построить вписанную окружность в треугольник, требуется выполнить следующие шаги:

Пример 1:

Построить вписанную окружность в треугольник ABC, где AB = 6 см, BC = 8 см, AC = 10 см.

Решение:

1. Найдите полупериметр треугольника: p = (AB + BC + AC) / 2 = (6 + 8 + 10) / 2 = 12 см.

2. Вычислите радиус вписанной окружности: r = sqrt((p - AB) * (p - BC) * (p - AC) / p) = sqrt((12 - 6) * (12 - 8) * (12 - 10) / 12) = 2 см.

3. Найдите координаты центра вписанной окружности: x = (AB * P1 + BC * P2 + AC * P3) / (P1 + P2 + P3) = (6 * 0 + 8 * 6 + 10 * 8) / (0 + 6 + 8) = 7 см, y = (AB * Q1 + BC * Q2 + AC * Q3) / (Q1 + Q2 + Q3) = (6 * 2 + 8 * 0 + 10 * 4) / (2 + 0 + 4) = 5 см. Здесь P1, Q1 - координаты точки A, P2, Q2 - координаты точки B, P3, Q3 - координаты точки C.

4. Нарисуйте вписанную окружность с центром в точке (7, 5) и радиусом 2 см.

Пример 2:

Построить вписанную окружность в треугольник ABC, где AB = 5 см, BC = 7 см, AC = 9 см.

Решение:

1. Найдите полупериметр треугольника: p = (AB + BC + AC) / 2 = (5 + 7 + 9) / 2 = 10 см.

2. Вычислите радиус вписанной окружности: r = sqrt((p - AB) * (p - BC) * (p - AC) / p) = sqrt((10 - 5) * (10 - 7) * (10 - 9) / 10) = 1 см.

3. Найдите координаты центра вписанной окружности: x = (AB * P1 + BC * P2 + AC * P3) / (P1 + P2 + P3) = (5 * 0 + 7 * 6 + 9 * 7) / (0 + 6 + 7) = 7 см, y = (AB * Q1 + BC * Q2 + AC * Q3) / (Q1 + Q2 + Q3) = (5 * 2 + 7 * 0 + 9 * 5) / (2 + 0 + 5) = 5 см. Здесь P1, Q1 - координаты точки A, P2, Q2 - координаты точки B, P3, Q3 - координаты точки C.

4. Нарисуйте вписанную окружность с центром в точке (7, 5) и радиусом 1 см.

Практическое применение вписанной окружности

Вписанная окружность в треугольник имеет множество практических применений, которые могут быть полезными в повседневной жизни и различных областях деятельности.

Во-первых, знание о вписанной окружности треугольника может быть полезно в строительстве. Например, при проектировании крыши треугольного здания, вписанная окружность может помочь определить расположение опор или основных точек крепления, что повысит устойчивость и прочность конструкции.

Во-вторых, вписанная окружность может использоваться в геодезии. При построении графика крутых сегментов дороги, окружность, вписанная в треугольник, может помочь рассчитать радиус поворота и определить минимальную дугу для безопасного прохождения поворота.

Кроме того, вписанная окружность имеет применение в архитектуре. При проектировании строений или монументов, вписанная окружность может помочь определить гармоничные пропорции и симметрию, что способствует созданию эстетически привлекательных объектов.

И наконец, вписанная окружность имеет значимость в математике и геометрии, так как является одной из основных характеристик треугольника. Различные свойства вписанной окружности позволяют решать разнообразные задачи и расширяют понятия о треугольниках.

В целом, знание и использование вписанной окружности в треугольнике может приносить пользу в различных сферах и деятельности, способствуя решению задач и повышению качества проектирования и строительства.