Математика - это прекрасный предмет, который изучается практически везде, начиная с младших классов школы. Все мы знаем, что формулы - это основа математики. Они помогают нам решать различные задачи и находить ответы на интересующие вопросы.
Однако, что делать, когда нужно узнать объем формулы? Этот вопрос беспокоит многих учащихся и взрослых, которые сталкиваются с математическими задачами. В этой статье мы рассмотрим несколько простых шагов, которые помогут вам справиться с этой задачей.
Первым шагом для определения объема формулы является выделение ключевых понятий и переменных в задаче или формуле. Это поможет вам понять, какие параметры необходимы для расчета объема. Например, если речь идет о геометрической фигуре, вам понадобятся известные размеры, такие как длина, ширина и высота.
Вторым шагом будет использование соответствующей формулы для расчета объема. Все формулы доступны в учебнике по математике или в интернете. Не забудьте проверить ее правильность, чтобы избежать ошибок. Примените формулу, используя значения, которые вы выделили на предыдущем шаге, и выполните необходимые вычисления.
Наконец, третьим шагом будет оценка полученного результата. Убедитесь, что ваш ответ имеет смысл с точки зрения контекста задачи. Проведите проверку, применяя полученный объем к реальным данным или сравнивая с известными результатами, если это возможно. Таким образом, вы сможете убедиться, что все выполнено правильно и вы получили искомый объем формулы.
Зачем узнавать объем формулы?

Знание объема формулы помогает во многих областях. Например, в строительстве объем формулы используется для расчета необходимого количества материалов, таких как бетон, кирпичи или плитки. В физике объем формулы необходим для определения объема жидкостей или газов, а также для расчета плотности и массы тела.
Знание объема формулы также полезно в геометрии и алгебре. Объем формулы позволяет определить размеры объектов и рассчитать их свойства. Например, объем геометрических фигур, таких как сфера, цилиндр или параллелепипед, можно выразить с помощью соответствующих формул.
Кроме того, знание объема формулы помогает развить абстрактное мышление и логическое мышление. Расчет объема формулы требует анализа и применения математических принципов, что помогает развить навыки решения проблем.
Таким образом, узнавание объема формулы является важной задачей, которая имеет применение в различных областях науки и позволяет решать практические и теоретические задачи. Это навык, который помогает развить понимание математических концепций и развить умения анализировать и решать разнообразные задачи.
Важность понимания объема формулы

Размер формулы может варьироваться от простых до сложных. Понимание объема формулы поможет вам определить, сколько времени и усилий потребуется для решения задачи. Это позволит вам более эффективно планировать свою работу и избегать неприятных сюрпризов на поздних этапах.
Кроме того, понимание объема формулы поможет вам выбрать подходящий метод решения задачи. Если формула имеет большой объем, то может потребоваться использование компьютерных программ или математического программного обеспечения для быстрого и точного решения. Если формула имеет малый объем, то, возможно, ее можно решить ручным способом.
Также, знание объема формулы поможет вам структурировать свою работу и держать все под контролем. Вы можете разбить формулу на несколько частей и решать их по одной. Это облегчит процесс решения задачи и поможет избежать ошибок.
В целом, понимание объема формулы имеет большое значение для успешного решения задач и достижения желаемых результатов. Это является неотъемлемой частью овладения математическими и научными навыками, которые пригодятся вам на протяжении всей жизни.
Простые шаги для определения объема формулы
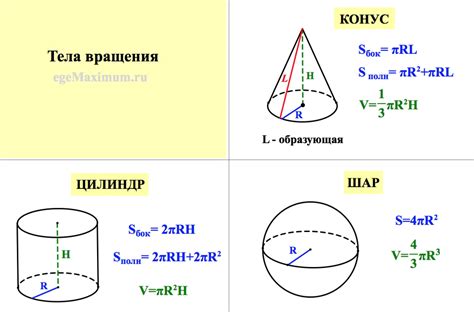
Определение объема формулы может быть полезным при проведении различных математических и физических расчетов. В данной статье рассмотрим несколько простых шагов, которые помогут вам определить объем формулы.
- Разбейте формулу на отдельные части
- Определите количество и типы переменных
- Оцените сложность каждой части
- Просуммируйте объем каждой части
- Проверьте правильность вычисления
Первый шаг состоит в разбиении формулы на отдельные части. Изучите формулу и определите, какие элементы она содержит. Разделите формулу на группы, каждая из которых будет иметь свою функцию.
После разделения формулы на части определите количество переменных, содержащихся в каждой части. Кроме того, определите типы переменных - это могут быть числа, буквы, функции и т.д.
Оцените сложность каждой части формулы. Определите, есть ли в ней операции сложения, вычитания, умножения, деления, возведения в степень или другие математические операции. Оценка сложности поможет вам понять, как много времени и усилий понадобится для вычисления формулы.
Сложите объем каждой части формулы, чтобы определить общий объем формулы. Объем можно определить, например, путем подсчета количества символов или путем оценки количества нужных операций.
В конце проверьте правильность вычисления объема формулы. Проверьте, правильно ли вы разбили формулу на части, верно ли определили количество и типы переменных и правильно ли посчитали объем каждой части. В случае ошибок повторите шаги сначала.
Следуя этим простым шагам, вы сможете определить объем формулы и использовать эту информацию для проведения необходимых математических или физических расчетов.
Определение объема формулы с помощью основных операций

Первым шагом при определении объема формулы является рассмотрение всех операций, которые входят в данное выражение. Затем следует определить, какие значения принимают операнды и какие значения имеют сама операция. Например, в случае сложения операндами являются числа, а операция возвращает сумму этих чисел.
После определения операций и их значений можно выполнять вычисления. Для этого необходимо применить операции в соответствии с их приоритетом. Например, умножение и деление выполняются перед сложением и вычитанием.
Если в формуле присутствуют скобки, то следует сначала выполнить операции внутри скобок, а затем продолжить вычисления по аналогии с предыдущим шагом.
После всех вычислений необходимо получить итоговый результат и оценить его объем. Если формула содержит большое количество операций и подвыражений, то ее объем будет значительно больше, чем у простых выражений.
Определение объема формулы с помощью основных операций является важным навыком при работе с математическими выражениями. Владение этими навыками помогает более эффективно решать задачи, связанные с математикой и наукоемкими дисциплинами.
Как определить объем формулы с использованием интеграла

Чтобы определить объем формулы с использованием интеграла, следуйте следующим шагам:
- Найдите границы интегрирования. Определите, где начинается и где заканчивается ваша формула в пространстве. На основе этих границ вы зададите пределы интегрирования.
- Выберите переменную интегрирования. Это может быть любая переменная в вашей формуле, обычно она связана с измерением длины, ширины или высоты объекта.
- Запишите формулу для вычисления объема. Определите зависимость между вашей переменной интегрирования и другими параметрами, которые определяют объем. Это может быть, например, площадь сечения объекта на определенной высоте.
- Интегрируйте формулу. Используйте определенные границы интегрирования и переменную интегрирования для расчета значения интеграла. Это даст вам объем вашей формулы.
Вычисление объема формулы с использованием интеграла является точным методом, который учитывает все особенности и форму фигуры. Этот метод может быть применен к многим различным типам формул, что делает его очень полезным инструментом для решения сложных задач.
Интересные примеры определения объема формулы

Определение объема формулы может быть интересным и запоминающимся опытом. Вот несколько примеров:
- Скалярное произведение двух векторов:
- Найти длину каждого вектора.
- Умножить эти длины.
- Найти косинус угла между векторами.
- Умножить результаты.
- Найти длину, ширину и высоту.
- Умножить эти значения.
- Найти площадь основания (площадь круга).
- Умножить площадь основания на высоту.
- Найти площадь основания (площадь круга).
- Умножить площадь основания на треть высоты.
Это лишь некоторые примеры, и существует множество других формул, которые можно определить объем. Интересные и необычные способы нахождения объема могут вызывать любопытство и помочь лучше запомнить соответствующие формулы.