Куб разности - это математическая операция, которая позволяет найти куб разницы двух чисел. Это полезное умение, которое может быть применено в различных ситуациях, например, при решении математических задач или при работе с геометрическими фигурами.
Процесс нахождения куба разности может показаться сложным, но на самом деле, он достаточно прост. Для того чтобы найти куб разности двух чисел, нужно сначала вычислить разность этих чисел, а затем возвести эту разность в куб. Это можно сделать с помощью специальной формулы.
Формула для нахождения куба разности:
(a - b)³ = a³ - 3a²b + 3ab² - b³
В этой формуле a и b - это числа, разность которых мы хотим найти. Подставив значения для a и b в формулу, мы можем найти результат.
Важно помнить, что данная формула работает только для куба разности. Для других степеней разности существуют другие формулы. Теперь, когда вы знаете, как найти куб разности, вы можете использовать это знание для решения различных математических задач и задач геометрии.
Имея разность двух чисел, как найти куб разности

Куб разности = c3
Пример:
- Пусть a = 5 и b = 3
- Выполняем операцию: c = a - b = 5 - 3 = 2
- Найдем куб разности: 23 = 2 * 2 * 2 = 8
Таким образом, куб разности чисел 5 и 3 равен 8.
Это простой способ найти куб разности двух чисел. Используя эту формулу, вы сможете легко найти куб разности любых двух чисел.
Формула для нахождения куба разности
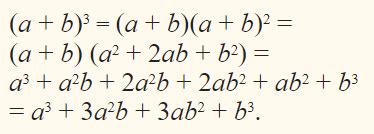
Для нахождения куба разности двух чисел, можно использовать следующую формулу:
Куб разности двух чисел a и b вычисляется как:
(a - b)³ = a³ - 3a²b + 3ab² - b³
Используя данную формулу, мы можем легко вычислить куб разности двух чисел. Просто подставьте значения чисел a и b в формулу и выполните необходимые арифметические операции.
Примеры применения нахождения куба разности в реальной жизни
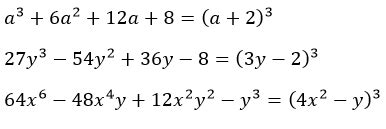
1. Физика и инженерия: Нахождение куба разности может быть полезным при решении проблем, связанных с механикой или электротехникой. Например, при расчете изменений во времени скорости или ускорения, а также при определении изменений в объеме или плотности материала с течением времени.
2. Экономика и финансы: Зная куб разности двух величин, можно определить, как изменится итоговая сумма или выгода в результате изменения этих величин. Например, при расчете увеличения прибыли от изменения цен на товары или услуги, а также при определении изменений в предложении и спросе.
3. Научные исследования: Нахождение куба разности может быть полезно при анализе и интерпретации данных в различных научных областях. Например, в биологии при изучении изменений в генетическом коде или в химии при определении изменений в концентрации вещества.
4. Криптография: Куб разности может использоваться для создания и анализа шифров. Это может быть полезно при разработке защитных механизмов и взломе кодов.
5. Математика и статистика: Нахождение куба разности может быть полезным для решения задач в математическом анализе, алгебре и статистике. Например, при изучении изменений функций, определении пространственной вариации данных или нахождении трендов и паттернов в статистических данных.
Все эти примеры демонстрируют, что нахождение куба разности имеет широкий спектр применений и может быть полезным в различных областях жизни и исследований.