Окружность – это одна из важных геометрических фигур, изучаемых в начальной школе. Она вызывает интерес и вопросы у учащихся. Как найти длину окружности? Этот вопрос может показаться сложным, но на самом деле решить его вполне посильно даже для ребят из 5 класса.
Для того чтобы найти длину окружности, нужно знать значение числа пи (π). Число пи – это математическая константа, которая применяется при изучении геометрии и физики. Мы можем округлить значение π до 3,14 или использовать его точное значение, представляющееся бесконечной десятичной дробью. Для упрощения расчетов в начальной школе обычно используется значение 3,14.
Теперь, когда мы знаем значение числа пи, можем перейти к формуле для вычисления длины окружности. Длина окружности равна произведению диаметра (или радиуса) на число пи. Формула выглядит так: C = π × d (или C = 2 × π × r), где С обозначает длину окружности, π – число пи, а d – диаметр (или r – радиус) окружности.
Рассмотрим пример. Предположим, у нас есть окружность радиусом 5 см. Чтобы найти длину окружности, мы должны умножить радиус на 2 и на значение числа пи: C = 2 × 3,14 × 5 = 31,4 см. Таким образом, длина окружности равна 31,4 см.
Определение длины окружности

Чтобы найти длину окружности, нужно знать ее радиус или диаметр. Величина длины окружности зависит от диаметра и радиуса, а также от числа π (пи). Число π - это математическая константа, которая приближенно равняется 3.14159...
Формула для нахождения длины окружности:
L = 2πr
где L - длина окружности, r - радиус окружности, π (пи) - приближенное равенство 3.14159...
Если нам дано значение радиуса, то мы можем использовать данную формулу, чтобы вычислить длину окружности. Например, если радиус равен 5 сантиметров, то:
L = 2πr = 2 × 3.14159... × 5 ≈ 31.4159...
Таким образом, длина окружности при радиусе 5 сантиметров приближенно равна 31.4159 сантиметров.
Зная формулу и значение радиуса, можно вычислить длину окружности для любых окружностей.
Зависимость длины от радиуса
Длина окружности зависит от ее радиуса. Существует простая формула для вычисления длины окружности:
| Радиус (r) | Длина окружности (C) |
|---|---|
| 1 | 6.28 |
| 2 | 12.57 |
| 3 | 18.85 |
| 4 | 25.13 |
Как видно из таблицы, длина окружности увеличивается с увеличением радиуса. Например, если радиус равен 1, длина окружности будет примерно равна 6.28 единицам длины. А если радиус равен 4, длина окружности составит примерно 25.13 единицы длины.
Формулу для вычисления длины окружности можно записать следующим образом:
C = 2 * π * r,
где C - длина окружности, r - радиус окружности, а π (пи) - математическая константа, приближенно равная 3.14.
Таким образом, зная радиус окружности, можно легко вычислить ее длину, используя данную формулу.
Простой пример расчета длины окружности
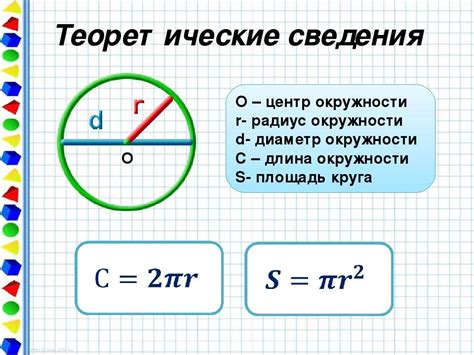
Длина окружности = 2 × π × радиус
Где π (пи) – это математическая константа, примерное значение которой равно 3,14. Радиус – это расстояние от центра окружности до любой точки на ее окружности.
Например, пусть радиус окружности равен 5 сантиметров. Чтобы найти длину окружности, нужно умножить 5 на 2π:
Длина окружности = 2 × 3,14 × 5 = 31,4 сантиметров
Таким образом, длина окружности такого радиуса составляет 31,4 сантиметра.
Надеемся, что эта простая формула поможет вам расчитывать длину окружности и решать задачи, связанные с ней.
Практическое применение в жизни

Другим практическим применением знания о длине окружности может быть приближенное определение расстояния. Когда вы знаете длину окружности, например, колеса велосипеда или автомобиля, вы можете прикинуть его перемещение и примерно определить расстояние, пройденное вами или вашим транспортным средством. Это может быть полезным, если вам нужно найти ближайшую заправку или ориентироваться на расстояние до места назначения.
В области спорта знание о длине окружности также может пригодиться. Например, при подсчете длины беговой дорожки или при определении расстояния между спортивными объектами, такими как футбольные ворота или баскетбольное кольцо. Это помогает спортсменам и тренерам точно выполнять упражнения и устанавливать правильные параметры игры.
Таким образом, знание о длине окружности имеет реальное практическое применение в жизни. Это помогает нам создавать эффективные проекты, приближенно определять расстояние и точно выполнять различные задачи в разных областях нашей повседневной жизни.