Одной из часто встречающихся задач в математике является поиск линейной функции по заданному графику. Это важное умение, которое позволяет предсказывать значения функции при различных аргументах и строить аналитическую модель для дальнейшего анализа данных. Но как же найти эту функцию без лишних усилий?
Для начала, необходимо вспомнить, что линейная функция представляет собой прямую линию на графике. Она имеет вид y = kx + b, где k - наклон прямой, а b - точка пересечения с осью ординат. Чтобы найти эти значения, нужно определить две точки на графике и вычислить соответствующие им значения x и y.
Наиболее простой способ найти две точки на графике - это выбрать две очевидные точки, через которые проходит прямая. Например, можно выбрать начало координат (0, 0) и точку с наибольшим или наименьшим значением y. Затем вычисляем соответствующие значения x и y для этих точек. Теперь мы имеем две точки и можем найти наклон прямой, а затем точку пересечения с осью ординат, подставив значения x и y в уравнение функции.
Определение линейной функции
Коэффициент наклона k отвечает за то, насколько быстро прямая растет или убывает. Если k положительный, то прямая будет возрастать слева направо, а если k отрицательный, то прямая будет убывать слева направо.
Коэффициент смещения b задает точку пересечения прямой с осью y. Если b положительный, то прямая будет пересекать ось y выше начала координат, а если b отрицательный, то прямая будет пересекать ось y ниже начала координат.
Определение линейной функции позволяет нам легко и быстро находить ее график, используя данные о значениях k и b. Это полезно, например, при анализе экономических и финансовых данных, моделировании процессов в физике или программировании.
Знакомство с графиком

График линейной функции представляет собой прямую линию, которая проходит через две точки. Для построения графика линейной функции необходимо знать как минимум две точки на этой прямой.
На графике линейной функции ось x обозначает входные значения, а ось y – выходные значения. Также на графике можно найти такие характеристики как наклон и смещение прямой.
Знакомство с графиком является первым шагом в поиске линейной функции по графику. Постройте график, изучите его форму и свойства, чтобы легко и быстро найти линейную функцию по графику.
Определение углового коэффициента
Угловой коэффициент обозначается символом "k" и вычисляется следующим образом:
k = (y2 - y1) / (x2 - x1)
где (x1, y1) и (x2, y2) - координаты двух точек на графике линейной функции.
Зная угловой коэффициент, можно определить наклон прямой. Если угловой коэффициент положительный, то прямая имеет положительный наклон (т.е. идет вверх отлево направо). Если угловой коэффициент отрицательный, то прямая имеет отрицательный наклон (т.е. идет вниз отлево направо).
Кроме того, если угловой коэффициент равен нулю, то прямая горизонтальна (параллельна оси абсцисс), а если он равен бесконечности, то прямая вертикальна (параллельна оси ординат).
Таким образом, угловой коэффициент помогает определить основные характеристики линейной функции и позволяет найти линейную функцию по ее графику легко и быстро.
Поиск точки пересечения с осью ординат
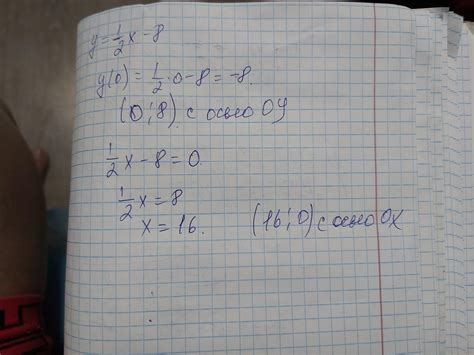
Чтобы найти точку пересечения с осью ординат для линейной функции, необходимо найти значение ординаты, при котором абсцисса равна нулю. Другими словами, для точки пересечения с осью ординат справедливо, что значение абсциссы равно нулю.
Для поиска точки пересечения с осью ординат у линейной функции, заданной уравнением y = kx + b, необходимо подставить вместо x значение 0 и решить уравнение по переменной y. Полученное значение y и будет ординатой точки пересечения с осью ординат.
Для наглядного представления найденной точки пересечения с осью ординат можно построить график функции и отметить на нем полученные координаты.
Приведем пример нахождения точки пересечения с осью ординат для функции y = 2x + 3:
| x | y |
| 0 | 3 |
Таким образом, точка пересечения с осью ординат для функции y = 2x + 3 имеет координаты (0, 3).
Определение уравнения прямой

Для определения уравнения прямой по ее графику важно иметь минимум две точки на этой прямой. Зная координаты этих точек, можно рассчитать коэффициент наклона m и свободный член b.
Для определения коэффициента наклона следует вычислить разность значений y и разделить ее на разность соответствующих значений x. То есть m = (y2 - y1) / (x2 - x1).
Для определения свободного члена b следует выбрать любую точку на прямой и подставить ее координаты и значение m в уравнение прямой. Например, если мы выбрали точку (x1, y1), то уравнение прямой примет вид y1 = m * x1 + b, откуда можно выразить b как b = y1 - m * x1.
Итак, для определения уравнения прямой по графику необходимо найти коэффициент наклона m и свободный член b, используя данные о точках на этой прямой. После этого можно записать уравнение прямой y = mx + b, где m и b являются найденными значениями.
Проверка результатов
После того, как вы нашли линейную функцию по графику, важно проверить правильность полученных результатов. Это поможет убедиться, что выбранная функция действительно описывает заданный график и даёт корректные значения для всех точек.
Первый шаг в проверке результатов - вычисление значений функции для нескольких точек на графике. Для этого выберите несколько произвольных значений для переменной x и подставьте их в вашу найденную функцию. Затем сравните полученные значения с соответствующими точками на графике. Если значения совпадают, это говорит о том, что функция правильно описывает график.
Однако, для полной уверенности в правильности результатов, необходимо также проверить свойства линейной функции. Например, убедитесь, что для функции y = kx + b коэффициент k соответствует наклону графика, а коэффициент b определяет точку пересечения графика с осью y. Если эти свойства не выполняются, это может говорить о том, что найденная функция не является линейной или не соответствует заданному графику.
Другим способом проверки результатов является построение обратного графика. Для этого необходимо выбрать несколько точек на графике и определить их координаты. Затем подставьте эти значения в формулу найденной функции и сравните результаты с соответствующими значениями переменной x. Если значения совпадают, это подтверждает правильность выбранной функции.
Важно помнить, что при проверке результатов необходимо учитывать возможные погрешности и ограничения метода. Например, если график имеет много точек, близких по координатам, или имеет "шум", то результаты могут быть неточными. В таких случаях рекомендуется использовать метод наименьших квадратов для поиска наилучшей линейной функции, а затем проводить дополнительные проверки для уточнения результатов.
Использование программных инструментов

Для нахождения линейной функции по заданному графику существуют различные программные инструменты, которые сделают эту задачу легкой и быстрой. Воспользовавшись ими, вы сможете точно определить уравнение нужной линейной функции.
Одним из таких инструментов является программное обеспечение для математического моделирования, например, MatLab или Wolfram Mathematica. С их помощью можно построить график заданных точек и затем аппроксимировать его линейной функцией. Эти программы предоставляют широкие возможности для работы с графиками и математическими моделями, и их использование позволит без труда найти нужную линейную функцию.
Еще одним полезным инструментом являются онлайн-калькуляторы, специально разработанные для решения таких задач. С их помощью можно загрузить график, выбрать точки, к которым нужно построить линейную функцию, и получить результат в виде уравнения этой функции. Это удобное и быстрое решение, особенно если вам нужно найти линейную функцию только один раз или не хотите устанавливать дополнительное программное обеспечение.
Также стоит упомянуть о возможностях таблиц и электронных таблиц. Если у вас уже есть набор данных, можно загрузить его в таблицу и использовать встроенные функции для аппроксимации графика. Например, Excel позволяет построить график и получить уравнение линейной функции, опираясь на заданные точки.
Все эти программные инструменты обладают удобным и интуитивно понятным интерфейсом, что делает процесс поиска линейной функции по графику доступным для всех пользователей, даже без глубоких знаний в математике.
Таким образом, с использованием программных инструментов можно произвести точную аппроксимацию линейной функции по заданному графику, что сделает этот процесс легким и быстрым. Выберите подходящее программное обеспечение для ваших нужд и начните работать с графиками прямо сейчас!
Примеры решения

Для наглядности рассмотрим несколько примеров, как можно найти линейную функцию по графику.
| Пример | График | Решение |
|---|---|---|
| Пример 1 |  | Из графика видно, что функция проходит через точку (2, 4). Также, мы можем обратить внимание, что при увеличении значения x на 1, значение y увеличивается на 2. Значит, угловой коэффициент равен 2. Функция будет иметь вид y = 2x + b. Чтобы найти свободный член b, можем использовать точку (2, 4). Подставим ее в уравнение: 4 = 2 * 2 + b. Решая данное уравнение, получаем b = 0. Таким образом, линейная функция по данному графику будет иметь вид y = 2x. |
| Пример 2 |  | Из графика видно, что функция проходит через точку (1, 3) и имеет угловой коэффициент -1/2. Значит, функция будет иметь вид y = -1/2x + b. Чтобы найти свободный член b, можем использовать точку (1, 3). Подставим ее в уравнение: 3 = -1/2 * 1 + b. Решая данное уравнение, получаем b = 5/2 = 2.5. Таким образом, линейная функция по данному графику будет иметь вид y = -1/2x + 2.5. |
| Пример 3 |  | Из графика видно, что функция проходит через точку (0, -1). Заметим, что значение y увеличивается на 3 при увеличении значения x на 1. Значит, угловой коэффициент равен 3. Функция будет иметь вид y = 3x + b. Чтобы найти свободный член b, можем использовать точку (0, -1). Подставим ее в уравнение: -1 = 3 * 0 + b. Решая данное уравнение, получаем b = -1. Таким образом, линейная функция по данному графику будет иметь вид y = 3x - 1. |
Практическое применение

Навык быстрого и точного нахождения линейной функции по графику представляет большую практическую пользу в различных сферах деятельности. Вот несколько примеров, где этот навык может быть полезен.
Финансы и экономика: При анализе финансовых данных и экономических показателей может потребоваться определить зависимость между двумя переменными. Нахождение линейной функции по графику поможет установить связь и предсказать будущие значения.
Инженерия: В инженерии часто возникает необходимость оценить взаимосвязь между различными параметрами. Линейная функция позволяет определить эту зависимость и применить ее для решения различных задач.
Социология и маркетинг: Исследователи и маркетологи часто используют линейные функции для измерения и предсказания влияния различных факторов на поведение и предпочтения аудитории. Нахождение линейной функции по графику позволяет провести точный анализ и принять обоснованные решения.
Образование: Учебные программы по математике часто включают изучение линейных функций. Навык быстрого и точного нахождения линейной функции по графику помогает ученикам лучше понимать материал, решать задачи и успешно справляться с экзаменами.
Во всех этих ситуациях навык нахождения линейной функции по графику будет полезным для анализа данных, создания моделей и принятия обоснованных решений.
Советы и рекомендации

1. Анализируйте экстремумы графика:
Обратите внимание на точки, в которых график функции достигает максимального или минимального значения. Если график имеет только один экстремум, это может означать, что функция является прямой линией. В этом случае, чтобы найти угловой коэффициент, можно использовать любые две пары координат этих экстремумов.
2. Используйте формулу для нахождения углового коэффициента:
Угловой коэффициент линейной функции может быть найден с помощью формулы m = (y2 - y1) / (x2 - x1), где m - угловой коэффициент, а (x1, y1) и (x2, y2) - координаты двух точек на графике. Зная угловой коэффициент, мы можем записать линейную функцию в виде уравнения y = mx + b, где b - точка пересечения графика с осью y.
3. Проверяйте полученное уравнение, используя другие точки:
Если у вас есть доступ к нескольким дополнительным точкам на графике, проверьте, что полученное уравнение линейной функции работает для них. Подставьте координаты точек в уравнение и убедитесь, что обе части равны друг другу.
4. Используйте инструменты и онлайн-ресурсы:
Если у вас возникли трудности при нахождении линейной функции по графику, можно воспользоваться специальными онлайн-ресурсами и инструментами. Некоторые ресурсы позволяют построить график и автоматически найти соответствующую линейную функцию.
5. Постоянно тренируйтесь:
Нахождение линейной функции по графику требует практики и опыта. Чем больше задач вы решаете, тем легче будет вам справиться с этой задачей. Постоянно тренируйтесь на реальных или вымышленных графиках, чтобы стать более опытным в нахождении линейной функции.