Абсциссой точки перегиба функции является значение аргумента, при котором изменяется выпуклость кривой графика функции. Точку перегиба можно определить с помощью вычисления второй производной функции и ее равенства нулю.

Для поиска абсциссы точки перегиба следует выполнить следующие шаги:

1. Найти первую производную функции. Для этого необходимо применить правила дифференцирования для данной функции.

2. Найти вторую производную. Для этого нужно продифференцировать первую производную, полученную на предыдущем шаге.

3. Приравнять вторую производную нулю и решить получившееся уравнение относительно аргумента функции.

4. Найти значения функции в точке перегиба, подставив полученную абсциссу в исходную функцию.

Таким образом, выполнение указанных шагов позволит найти абсциссу точки перегиба функции. Знание этой характеристики позволяет более точно исследовать поведение графика функции и определить особенности ее изменения.

Как найти абсциссу точки перегиба функции?

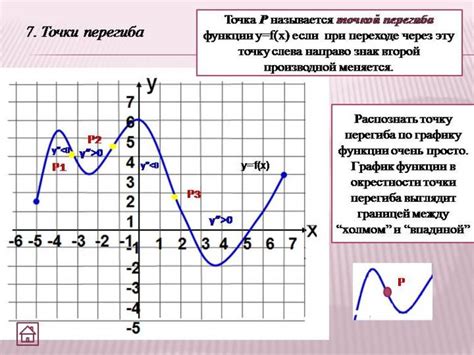
Для определения абсциссы точки перегиба функции нужно выполнить несколько шагов. Вот некоторые из них:

1. Найдите вторую производную функции. Для этого возьмите первую производную функции и продифференцируйте ее снова.
2. Решите уравнение, полученное приравнивании второй производной к нулю. Обратите внимание, что это уравнение может иметь несколько корней.
3. Подставьте найденные значения аргумента в первую производную функции и определите знаки производной в окрестности этих точек. Используйте метод интервалов для определения поведения функции.
4. Из анализа знаков производной определите, какое поведение функции соответствует каждому корню. Если функция меняет свой характер поведения с выпуклой на вогнутую или наоборот, то это абсцисса точки перегиба.

Итак, найдя абсциссы точек перегиба, вы сможете лучше понять поведение функции и использовать эту информацию для решения различных задач.

Поиск абсциссы точки перегиба

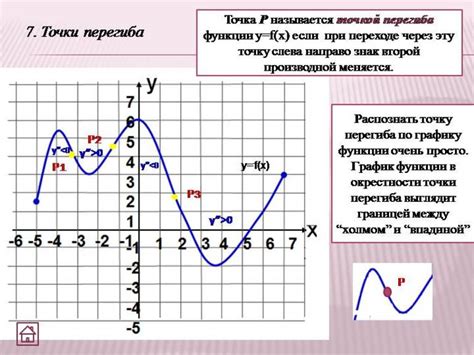
Для нахождения абсциссы точки перегиба можно использовать производные функции. Первая производная позволяет определить, где функция меняет свой характер (выпуклость или вогнутость), а вторая производная дает информацию о том, в какой точке происходит эта смена.

Алгоритм поиска абсциссы точки перегиба включает следующие шаги:

1. Найдите первую производную функции.
2. Проведите анализ знаков первой производной, чтобы определить интервалы, на которых функция возрастает или убывает.
3. Найдите вторую производную функции.
4. Проанализируйте знаки второй производной на каждом из интервалов из пункта 2. Если знак второй производной меняется с плюса на минус или наоборот, то в этой точке происходит смена выпуклости или вогнутости кривой.
5. Вычислите абсциссы точек перегиба, найдя значения x, при которых производная равна нулю или не существует.

Используя данный алгоритм и проведя анализ знаков производных, можно найти абсциссы точек перегиба функции.