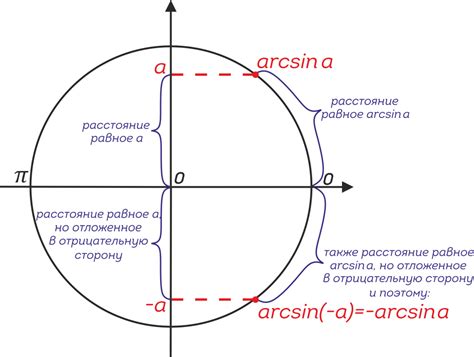
Арксинус - это обратная функция к синусу. В математике для обозначения арксинуса используется обозначение sin-1 или asin. Арксинус позволяет нам найти угол, значение синуса которого равно данному числу. Если синус угла равен x, то арксинус x будет равен этому углу. То есть, арксинус принимает значение x и возвращает угол, синус которого равен x.
Одним из способов нахождения арксинуса через синус является использование тригонометрического идентичности. Тригонометрическая идентичность гласит, что арксинус от синуса угла равен самому углу:
asin(sin(a)) = a
При этом значение арксинуса может варьироваться в диапазоне от -π/2 до π/2 радиан или от -90° до 90° градусов, так как синус угла может иметь значения от -1 до 1.
Рассмотрим пример. Пусть нам нужно найти арксинус синуса 0.5:
asin(sin(0.5)) = 0.5
Таким образом, арксинус от синуса угла 0.5 равен самому углу 0.5. Это можно проверить с помощью калькулятора или специальной программы для вычисления тригонометрических функций.
Синус и арксинус: основные понятия
Значение синуса может варьироваться от -1 до 1, где -1 соответствует треугольнику, у которого противолежащая сторона равна его гипотенузе, а 1 - треугольнику, у которого противолежащая сторона равна 0.
Арксинус - это обратная функция к синусу. Он позволяет найти угол, который имеет данный синус. В математической нотации арксинус обозначается как arcsin или sin-1.
Значение арксинуса также находится в диапазоне от -1 до 1, но выражается в радианах. Отличием арксинуса от синуса является то, что арксинус не является периодической функцией и имеет область определения от -1 до 1. Возвращает арксинус значения синуса в диапазоне от -π/2 до π/2.
Формула для нахождения арксинус через синус

arcsin(x) = sin-1(x)
Здесь x - значение синуса, которое мы хотим найти. В математическом обозначении арксинус обычно обозначается так: arcsin(x) или sin-1(x).
Для использования этой формулы необходимо знать значение синуса, чтобы найти соответствующий угол.
Например, если нам известно, что sin(x) = 0.5, мы можем использовать формулу арксинуса, чтобы найти угол:
arcsin(0.5) = sin-1(0.5)
Затем, используя таблицу значений синуса или калькулятор, мы находим угол, при котором sin(x) = 0.5:
arcsin(0.5) = 30°
Таким образом, arcsin(0.5) = 30°.
Формула для нахождения арксинуса через синус очень полезна при решении различных задач, связанных с геометрией, физикой и другими науками.
Как найти арксинус через синус: шаги и примеры

Для того чтобы найти арксинус через синус, следуйте этим шагам:
- Убедитесь, что значение синуса находится в диапазоне от -1 до 1. Если значение синуса выходит за этот диапазон, то арксинус не определен.
- Используя таблицу значений или калькулятор, найдите арксинус для заданного значения синуса. Обычно значения арксинуса выражают в градусах или радианах.
Вот пример:
Пусть у нас есть значение синуса равное 0.5. Мы хотим найти соответствующий угол.
Шаг 1: Проверим, что значение синуса находится в диапазоне от -1 до 1. 0.5 находится в этом диапазоне, поэтому мы можем продолжать.
Шаг 2: Используя таблицу или калькулятор, найдем арксинус для значения 0.5. В данном случае, арксинус равен 30 градусам или π/6 радиан.
Таким образом, угол, синус которого равен 0.5, равен 30 градусам или π/6 радиан.
Применение арксинуса в задачах и уравнениях

Применение арксинуса может быть полезно в решении различных задач и уравнений. Например, если нам известно значение синуса некоторого угла, мы можем найти этот угол, используя арксинус.
Для примера рассмотрим уравнение sin(x) = 0.5. Мы хотим найти все значения x, удовлетворяющие этому уравнению. Для этого мы применяем арксинус к обеим сторонам уравнения:
arcsin(sin(x)) = arcsin(0.5)
Поскольку арксинус и синус являются обратными функциями, они сокращаются, и уравнение становится:
x = arcsin(0.5)
Таким образом, мы получили, что x равно арксинусу от 0.5. Мы можем использовать тригонометрические таблицы или калькуляторы, чтобы найти значение арксинуса от 0.5, которое составляет около 30 градусов.
Также арксинус может быть полезен в задачах на построение треугольников. Например, если нам известны значения двух сторон треугольника и угол между ними, мы можем использовать синусный закон для нахождения третьей стороны.
В общем, применение арксинуса в задачах и уравнениях позволяет нам находить значения углов и сторон в треугольниках, а также решать уравнения, связанные с тригонометрическими функциями.
Ограничения и особенности использования арксинуса
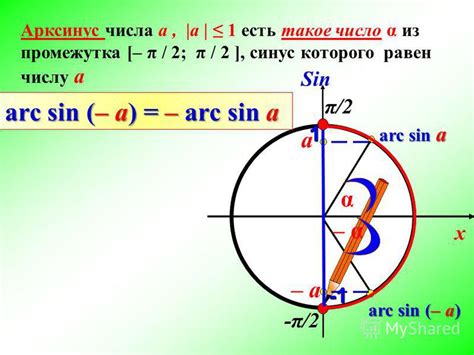
- Диапазон значений арксинуса ограничен от -π/2 до π/2.
- Арксинус сопоставляет углу его синус, поэтому разные углы с одинаковым синусом могут иметь разные значения арксинуса.
- Арксинус может быть выражен в радианах или градусах, поэтому необходимо учитывать используемую систему измерений.
- Арксинус является нестрого возрастающей функцией, то есть с увеличением значения синуса, значение арксинуса также увеличивается.
- Функция арксинус является неограниченной и имеет бесконечное количество значений.
- Использование арксинуса требует осторожности при работе с комплексными числами, так как арксинус может принимать комплексные значения.
- При использовании арксинуса необходимо учитывать неоднозначность значения, так как синус - периодическая функция с периодом 2π.
Все эти особенности и ограничения должны быть учтены при решении уравнений или задач, в которых встречается арксинус.
Интересные факты о арксинусе и синусе
1. Результат арксинуса всегда выражается в радианах.
2. Значение арксинуса лежит в диапазоне от -π/2 до π/2.
3. Значение синуса для арксинуса может быть от -1 до 1.
4. Арксинус является нелинейной функцией, то есть, график функции не является прямой линией.
5. Арксинус является частью группы тригонометрических функций, включающей также синус, косинус и тангенс.
6. Функция арксинуса широко применяется в геометрии, физике и инженерии для нахождения углов и решения тригонометрических задач.
7. Арксинус также часто используется в компьютерной графике для создания плавных анимаций и эффектов.
8. Синус - это основная тригонометрическая функция, которая описывает соотношение между стороной прямоугольного треугольника и его гипотенузой.
9. Значение синуса может быть от -1 до 1.
10. График функции синуса представляет собой периодическую кривую, которая повторяется каждые 360 градусов или 2π радиан.
Сравнение арксинуса с другими тригонометрическими функциями

Помимо арксинуса, в тригонометрии существуют и другие обратные тригонометрические функции, такие как арккосинус (acos), арктангенс (atan) и арккотангенс (acot). Все эти функции имеют свои особенности и использование в зависимости от конкретных задач.
Арксинус отличается от других обратных тригонометрических функций тем, что он применяется для нахождения угла, когда известно значение синуса. Он обозначается как arcsin или sin-1. Арксинус возвращает значение угла в радианах в пределах от -π/2 до π/2.
| Функция | Обозначение | Область значений |
|---|---|---|
| Арксинус | arcsin(x) или sin-1(x) | -π/2 ≤ x ≤ π/2 |
| Арккосинус | acos(x) или cos-1(x) | 0 ≤ x ≤ π |
| Арктангенс | atan(x) или tan-1(x) | -π/2 |
| Арккотангенс | acot(x) или cot-1(x) | 0 |
Важно заметить, что значения аргументов и области определения обратных тригонометрических функций могут меняться в зависимости от выбранной системы измерения углов (радианы или градусы), поэтому необходимо учитывать этот факт при использовании данных функций в практических расчетах.
Ссылки и дополнительные источники

Если вам интересна эта тема и вы хотите узнать больше о нахождении арксинуса через синус, рекомендуем вам обратиться к следующим источникам:
| Арксинус на Википедии | В статье на Википедии вы найдете более подробное описание арксинуса и его свойств. |
| Математика 24 - статья про арксинус | На сайте "Математика 24" вы найдете замечательную статью, объясняющую, что такое арксинус и как им пользоваться. |
| Математический портал "Математика онлайн" - арксинус | Математический портал "Математика онлайн" также предлагает понятное объяснение арксинуса и его использования. |
Эти ресурсы помогут вам повысить вашу математическую эрудицию и лучше понять арксинус как функцию синуса.