Биссектриса прямоугольного треугольника – это линия, которая делит угол треугольника на два равных угла. Нахождение биссектрисы очень полезно в различных задачах геометрии и тригонометрии. Чтобы найти биссектрису прямоугольного треугольника, необходимо применить некоторые формулы и использовать определенные шаги.
Для начала, найдите длины всех сторон треугольника. Затем используйте известные формулы для нахождения полупериметра треугольника и его площади. После этого можно приступить к вычислению биссектрисы.
Формула для нахождения биссектрисы прямоугольного треугольника имеет вид: биссектриса = (2 * √(a * b * p * (p - c))) / (a + b), где a и b – длины катетов треугольника, c – длина гипотенузы, а p – полупериметр.
Теперь, когда у вас есть формула и все необходимые значения, просто подставьте их в уравнение и выполните все необходимые вычисления. Результатом будет длина биссектрисы прямоугольного треугольника. Следуя этой формуле и шагам руководства, вы сможете легко и точно найти биссектрису любого заданного прямоугольного треугольника.
Что такое биссектриса треугольника
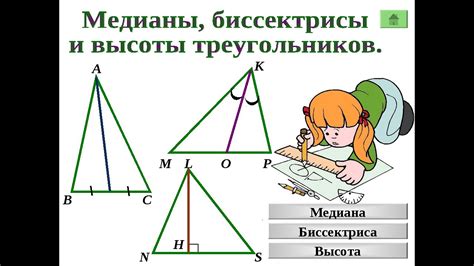
Биссектриса треугольника является важным элементом, который позволяет нам решать различные геометрические задачи и находить недостающие значения в треугольнике. Например, зная длину биссектрисы и одного из углов треугольника, можно вычислить длины сторон треугольника и другие углы. Также, биссектриса треугольника используется для построения вписанной окружности и для определения высоты треугольника.
Для нахождения биссектрисы одного из углов треугольника мы можем использовать формулу, которая основана на теореме синусов и длинах сторон треугольника. Зная длины двух сторон треугольника и величину одного из углов, можно вычислить длину биссектрисы. Формула для вычисления биссектрисы треугольника может быть применена к различным типам треугольников, включая прямоугольные треугольники.
Изучение биссектрисы треугольника помогает углубить понимание геометрии и найти решение для различных математических задач. Знание основных свойств и формул, связанных с биссектрисой, позволяет нам более глубоко анализировать треугольники и применять их свойства в практических задачах и конструкциях.
Свойства биссектрисы прямоугольного треугольника
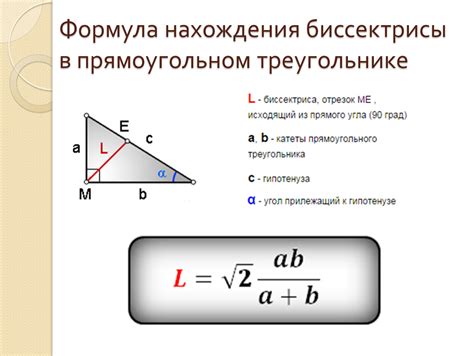
Свойства биссектрисы прямоугольного треугольника:
- Биссектриса является внутренней биссектрисой прямого угла треугольника, поскольку делит прямой угол равно на две части.
- Биссектриса является угловым биссектором, так как делит один из острых углов на две равные части.
- Биссектриса перпендикулярна противоположной стороне, что означает, что угол между биссектрисой и противоположной стороной равен 90 градусам.
Знание свойств биссектрисы прямоугольного треугольника позволяет использовать биссектрису для решения задачи, например, для нахождения середины гипотенузы или отношения сторон треугольника.
Расчет и использование биссектрисы прямоугольного треугольника помогают в решении различных геометрических задач и нахождении дополнительных свойств этого треугольника.
Формула для вычисления биссектрисы прямоугольного треугольника
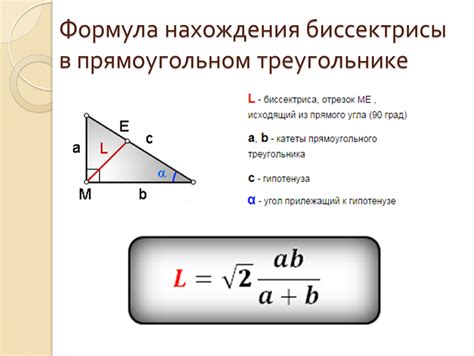
Пусть у нас есть прямоугольный треугольник с катетами a и b, и гипотенузой c. Формула для вычисления биссектрисы треугольника выглядит следующим образом:
| Формула | Пример | |
|---|---|---|
| b1 = (2 * a * b) / (a + b + c) | Если a = 3, b = 4, и c = 5, тогда b1 = (2 * 3 * 4) / (3 + 4 + 5) = 24 / 12 = 2 |
Таким образом, для нашего примера, длина биссектрисы прямоугольного треугольника равна 2.
Используя данную формулу, вы можете легко вычислить длину биссектрисы прямоугольного треугольника, зная значения катетов и гипотенузы треугольника.
Как найти биссектрису прямоугольного треугольника по длинам его сторон
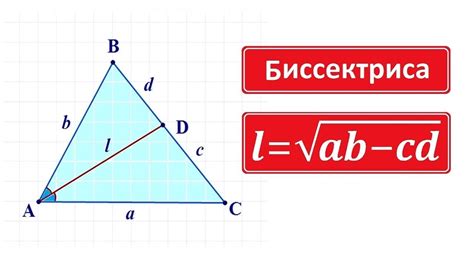
Биссектриса = √ [(a*b*(a+b)) / (a^2 + b^2 + 2ab)], где a и b - длины катетов прямоугольного треугольника.
Давайте рассмотрим пример. Пусть у нас есть прямоугольный треугольник со сторонами a = 3 и b = 4. Чтобы найти биссектрису, подставим значения в формулу:
| Формула | Расчет |
|---|---|
| Биссектриса = √ [(a*b*(a+b)) / (a^2 + b^2 + 2ab)] | Биссектриса = √ [(3*4*(3+4)) / (3^2 + 4^2 + 2*3*4)] |
| Биссектриса = √ [84 / 49] | |
| Биссектриса = √ 1.7143 | |
| Биссектриса ≈ 1.309 |
Таким образом, биссектриса прямоугольного треугольника со сторонами a = 3 и b = 4 примерно равна 1.309 единицам длины.
Используя данную формулу, вы можете легко найти биссектрису любого прямоугольного треугольника, если известны длины его сторон.
Как построить биссектрису прямоугольного треугольника
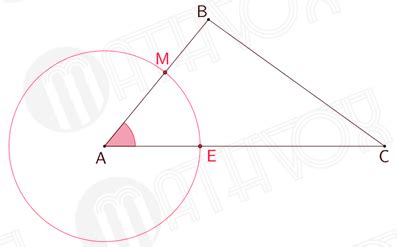
Чтобы построить биссектрису прямоугольного треугольника, выполните следующие шаги:
- Возьмите треугольник ABC, где угол B является прямым углом.
- Из точки B проведите прямую линию, проходящую через середину стороны AC (обозначим эту точку как D) и пересекающую противоположную сторону AB в точке E. Это будет биссектриса угла B.
- Измерьте равные расстояния от точки D до точек A и C и отметьте эти точки (обозначим их как F и G соответственно).
- Проведите прямые линии, соединяющие точки F и E, а также точки G и E. Эти линии будут пересекаться в точке H, которая является вершиной биссектрисы угла B.
Теперь вы построили биссектрису прямоугольного треугольника. Эта линия разделит угол B на две равные части. Используйте эту информацию при решении геометрических задач или для выполнения других задач, связанных с прямоугольными треугольниками.
Примеры решения задач с поиском биссектрисы прямоугольного треугольника
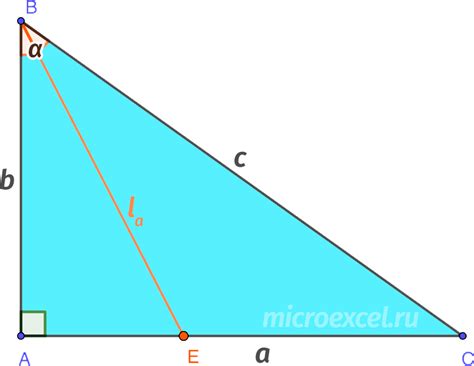
Чтобы найти биссектрису прямоугольного треугольника, мы можем использовать формулу, которая основана на свойствах треугольников. Рассмотрим несколько примеров решения задач с поиском биссектрисы:
| Пример | Условия | Решение |
|---|---|---|
| Пример 1 | Дан прямоугольный треугольник ABC, где AB = 3, AC = 4, BC = 5. | Сначала находим полупериметр треугольника по формуле: P = (AB + AC + BC) / 2 = (3 + 4 + 5) / 2 = 6.5. Затем находим площадь треугольника по формуле Герона: S = sqrt(P * (P - AB) * (P - AC) * (P - BC)) = sqrt(6.5 * (6.5 - 3) * (6.5 - 4) * (6.5 - 5)) = 6. Далее находим высоту треугольника, проведенную к гипотенузе по формуле: h = 2 * S / BC = 2 * 6 / 5 = 2.4. |
| Пример 2 | Дан прямоугольный треугольник DEF, где DE = 12, DF = 5, EF = 13. | Аналогично предыдущему примеру: Находим полупериметр P = (DE + DF + EF) / 2 = (12 + 5 + 13) / 2 = 15. Находим площадь S = sqrt(P * (P - DE) * (P - DF) * (P - EF)) = sqrt(15 * (15 - 12) * (15 - 5) * (15 - 13)) = 60. Находим высоту треугольника h = 2 * S / EF = 2 * 60 / 13 = 9.23. |
Приведенные примеры демонстрируют этапы решения задачи по поиску биссектрисы прямоугольного треугольника, используя соответствующие формулы. Во всех случаях необходимо вычислить полупериметр, площадь, высоту треугольника и найти длину биссектрисы с использованием заданных сторон треугольника. Округлите ответы до нужного числа знаков после запятой, если это необходимо.
Практическое применение биссектрисы прямоугольного треугольника
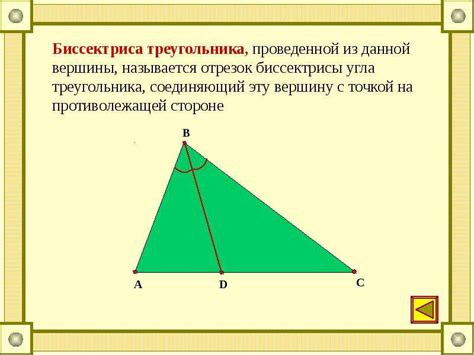
1. Определение центра вписанной окружности: Биссектрисы прямых углов прямоугольного треугольника пересекаются в центре окружности, вписанной в данный треугольник. Этот центр также является точкой пересечения биссектрисы угла, образованного сторонами треугольника и прямым углом. Нахождение центра вписанной окружности может быть полезно для решения геометрических задач.
2. Разделение сторон треугольника: Биссектриса гипотенузы прямоугольного треугольника делит эту сторону на две части в пропорции с длинами прилегающих к ней катетов. Это свойство можно использовать, чтобы разделить сторону треугольника на известные пропорции, что может быть полезно при конструировании или нахождении неизвестных значений.
3. Вычисление площадей: Биссектриса прямого угла прямоугольного треугольника может быть использована для вычисления площади треугольника, зная длины всех его сторон. Это может быть полезно при решении задач, связанных с площадями и нахождением неизвестных значений.
Знание о практическом применении биссектрисы прямоугольного треугольника может быть полезно как в школьном математическом образовании, так и в реальной жизни при решении геометрических задач и конструкций.