Прямоугольный треугольник – это треугольник, у которого один из углов равен 90 градусам. При решении задач по геометрии часто требуется найти различные характеристики треугольника, включая его биссектрисы. Биссектриса – это прямая, которая делит угол пополам. Если найти биссектрису прямоугольного треугольника из прямого угла, то можно решить множество задач, связанных с этим треугольником.
Чтобы найти биссектрису прямоугольного треугольника, необходимо знать его стороны и углы. Используя свойства прямоугольного треугольника, можно с легкостью получить уравнения для нахождения биссектрис. В основе этих уравнений лежат теоремы о перпендикулярных (по условию прямой в нашем случае) и равных углах.
Процесс нахождения биссектрисы прямоугольного треугольника из прямого угла состоит из нескольких шагов. Сначала находим длины сторон треугольника, а затем используем эти данные для нахождения углов. Затем применяется теорема о равных углах и формула биссектрисы для получения искомой прямой. Чтобы получить более точные результаты, рекомендуется использовать дополнительные формулы и свойства прямоугольных треугольников.
Определение биссектрисы прямоугольного треугольника
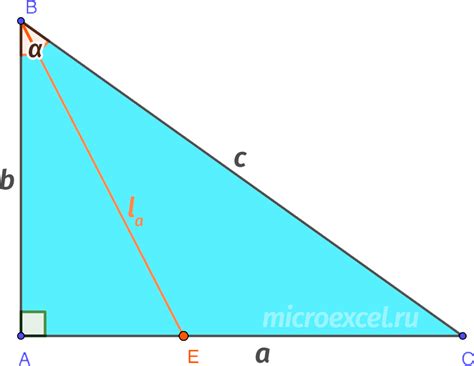
Чтобы найти биссектрису прямоугольного треугольника, следуйте этим шагам:
- Найдите длину гипотенузы прямоугольного треугольника.
- Разделите длину гипотенузы на 2.
- Из точки, где биссектриса пересекается с гипотенузой, проведите перпендикуляр к гипотенузе.
Таким образом, биссектриса будет проходить через вершину прямого угла и делить его на два равных угла.
Для лучшего понимания процесса определения биссектрисы прямоугольного треугольника, рассмотрим таблицу с примером:
| Сторона | Длина |
|---|---|
| Катет A | 5 |
| Катет B | 12 |
| Гипотенуза C | 13 |
| Биссектриса | 6.5 |
В данном примере, гипотенуза C имеет длину 13. Половина этой длины равна 6.5. Биссектриса пересекает гипотенузу в точке с координатой (6.5, 0). От этой точки проводится перпендикуляр к гипотенузе, который является биссектрисой прямого угла треугольника.
Определение биссектрисы
Чтобы найти биссектрису прямоугольного треугольника из прямого угла, можно воспользоваться следующей формулой:
Биссектриса = (a * c) / (a + b)
Где:
- a - это катет прямоугольного треугольника, смежный с прямым углом
- b - это другой катет прямоугольного треугольника
- c - это гипотенуза прямоугольного треугольника
Таким образом, зная значения сторон треугольника, можно вычислить биссектрису прямого угла.
Формула для вычисления биссектрисы

Для нахождения биссектрисы прямого угла прямоугольного треугольника можно использовать следующую формулу:
биссектриса = (a * c) / (a + c)
где:
- а - катет треугольника, смежный с искомой биссектрисой;
- c - гипотенуза треугольника.
Данная формула основана на свойствах прямоугольных треугольников и тригонометрических соотношениях. Она позволяет находить длину биссектрисы прямого угла треугольника без необходимости использования сложных тригонометрических функций.
Полученное значение биссектрисы можно использовать для решения различных задач, связанных с треугольниками, например, для вычисления площади треугольника или нахождения углов треугольника.
Формула Пифагора

Формула выглядит следующим образом:
c² = a² + b²
где c - длина гипотенузы, а a и b - длины катетов.
Исходя из формулы Пифагора, можно легко найти биссектрису прямоугольного треугольника из прямого угла. Биссектриса проходит из вершины прямого угла через середину гипотенузы и делит ее на две равные части.
Способы нахождения биссектрисы треугольника

Существует несколько способов определения биссектрисы треугольника:
- Геометрический метод: для нахождения биссектрисы из прямого угла прямоугольного треугольника нужно провести луч, который делит этот угол пополам и пересекает противоположную сторону в точке. Эта точка становится вершиной биссектрисы, а луч сам является ей.
- Тригонометрический метод: для треугольника ABC с прямым углом в точке C можно найти биссектрису из прямого угла, используя тангенс. Если угол A равен α, угол B равен β, а и b – длины сторон, инцидентных прямому углу, то биссектриса будет равна (а * tan(β/2)) / (tan(α/2) + tan(β/2)).
- Использование высот треугольника: еще один способ для нахождения биссектрисы треугольника – это использовать свойства высоты (перпендикуляр, проведенный из вершины прямого угла к гипотенузе) и половинного периметра треугольника. Перпендикуляр можно разделить на две части, используя соотношение длин сторон прямоугольного треугольника.
Это лишь несколько способов нахождения биссектрисы треугольника, и в зависимости от конкретных условий задачи может применяться другой метод. Важно точно определить задачу и выбрать соответствующий способ нахождения биссектрисы, чтобы получить нужный результат.
Использование угловых точек
Чтобы использовать угловые точки, необходимо знать, что биссектриса прямоугольного треугольника из прямого угла делит этот угол на два равных угла. Используя эту информацию, мы можем построить специальные точки, из которых мы проведем биссектрису.
Первой угловой точкой будет середина гипотенузы. Для ее нахождения, мы должны разделить гипотенузу пополам.
Вторая угловая точка будет являться основанием перпендикуляра, проведенного из вершины прямого угла на гипотенузу.
После нахождения этих двух точек, мы можем провести линию между ними, которая будет являться биссектрисой прямого угла. Для этого необходимо использовать линейку или другой инструмент для проведения линий.
Использование угловых точек позволяет легко и точно находить биссектрисы прямоугольных треугольников из прямых углов. Этот метод может быть полезен для решения геометрических задач и построения треугольников с заданными параметрами.
Пример расчета биссектрисы прямоугольного треугольника
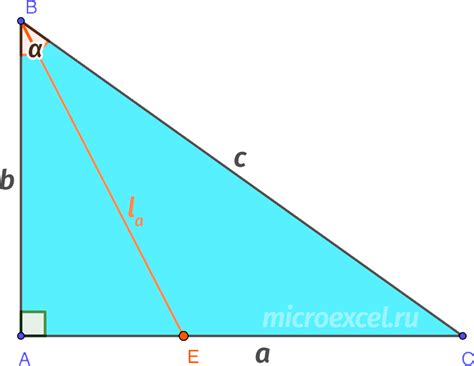
Для нахождения биссектрисы прямоугольного треугольника из прямого угла можно воспользоваться следующей формулой:
| Величина | Формула |
|---|---|
| Биссектриса прямого угла (b) | b = a * (c / (a + c)) |
где:
- a - длина катета, прилегающего к прямому углу
- c - длина гипотенузы
Давайте рассмотрим пример:
| Величина | Значение |
|---|---|
| Длина катета прилегающего к прямому углу (a) | 5 |
| Длина гипотенузы (c) | 13 |
Подставим значения в формулу:
b = 5 * (13 / (5 + 13))
(Исходные значения длин катета и гипотенузы взяты для примера, вы можете использовать свои значения)
Выполним вычисления:
b = 5 * (13 / 18)
b ≈ 3.611
Таким образом, биссектриса прямого угла прямоугольного треугольника, где длина катета прилегающего к прямому углу составляет 5, а длина гипотенузы равна 13, приближенно равна 3.611.
Пример с известными катетами

Рассмотрим пример, в котором известны значения катетов прямоугольного треугольника. Предположим, что один катет равен 4 см, а другой катет равен 3 см.
Для нахождения биссектрисы прямого угла треугольника воспользуемся формулой, которая гласит:
| Биссектриса прямого угла = (катет1 * катет2) / сумма катетов |
Подставляя в формулу известные значения, получаем:
| Биссектриса прямого угла = (4 см * 3 см) / (4 см + 3 см) = 12 см / 7 см ≈ 1.71 см |
Таким образом, в заданном примере биссектриса прямого угла прямоугольного треугольника равна примерно 1.71 см.
Практическое применение биссектрисы в геометрии

Одним из основных применений биссектрисы является определение точки пересечения этой биссектрисы с противоположной стороной треугольника. Эта точка называется центром вписанной окружности и часто используется для решения задач, связанных с треугольниками.
| Применение | Описание |
|---|---|
| Расчет площади треугольника | Биссектриса позволяет разбить треугольник на два равных меньших треугольника, что упрощает расчет площади с использованием формулы S = (1/2) * a * b * sin(C), где a и b - длины сторон, C - угол между этими сторонами. |
| Определение высоты треугольника | Биссектриса позволяет найти высоту треугольника, которая является перпендикулярной биссектрисе и проходит через вершину треугольника. Высота используется для расчета площади треугольника. |
| Нахождение биссектрисы прямоугольного треугольника | Биссектриса прямого угла делит противоположную катету пополам и является перпендикулярной гипотенузе. |
| Решение задачи на построение треугольника | Задачи по построению треугольника можно решить с использованием биссектрисы и других сторон и углов треугольника. |
Это лишь несколько примеров применения биссектрисы в геометрии. Важно понять, что биссектриса является мощным инструментом, который помогает в решении разнообразных задач и обнаружении свойств треугольников.
Построение биссектрисы треугольника
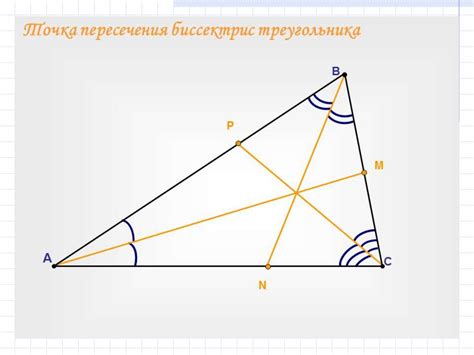
Для построения биссектрисы прямоугольного треугольника нам понадобится линейка и компас. Процедура построения следующая:
- Возьмите линейку и проведите отрезок, чтобы он пересекался с двумя сторонами треугольника. Этот отрезок будет основанием биссектрисы.
- Определите середину отрезка, используя компас, и пометьте ее.
- С помощью линейки и компаса постройте перпендикуляр к основанию биссектрисы, проходящий через пометку середины отрезка.
- Отметьте точку, в которой перпендикуляр пересекается с прямым углом треугольника.
- Проведите линию в соединяющую точку пересечения с прямым углом и вершину прямого угла треугольника. Эта линия будет являться биссектрисой треугольника.
Итак, зная процедуру построения биссектрисы треугольника, мы можем легко определить ее и в прямоугольном треугольнике из прямого угла. Это может быть полезно при решении задач и нахождении дополнительных углов треугольника.
Для построения достаточно нанести сегмент перпендикуляра, равный половине гипотенузы, на гипотенузу из ее середины. Точка пересечения с прямым углом будет определять конечную точку биссектрисы.
Таким образом, зная длину гипотенузы и используя простые геометрические принципы, можно найти биссектрису прямого угла в прямоугольном треугольнике.
Важно: Биссектриса, исходящая из прямого угла, является основой для нахождения других биссектрис треугольника. Таким образом, понимание этого принципа может быть полезно при решении более сложных задач геометрии.