Биссектриса равнобедренного треугольника – это отрезок, проходящий из вершины угла и делящий противоположную сторону на две равные части. Биссектриса является важной геометрической конструкцией, она не только делит сторону, но и делает угол между другими двумя сторонами равным.
Для того чтобы найти биссектрису равнобедренного треугольника, нужно знать его угол и длину равных сторон. Существует специальная формула для вычисления длины биссектрисы. Для этого делим произведение длин равных сторон на сумму длин равных сторон и получаем длину биссектрисы. Формула выглядит следующим образом:
Длина биссектрисы = (2 * √(a^2 - (b^2 / 4))) / (a + b)
Где a - длина равных сторон, b - длина противоположной стороны. Пользуясь этой формулой и зная длину сторон треугольника, можно легко вычислить длину биссектрисы.
Давайте рассмотрим пример. Предположим, у нас есть равнобедренный треугольник со сторонами длиной 8 см и противоположной стороной длиной 6 см. Чтобы найти длину биссектрисы, подставим значения в формулу:
Длина биссектрисы = (2 * √((8^2) - ((6^2) / 4))) / (8 + 6)
После выполнения всех вычислений получим:
Длина биссектрисы ≈ 4.82 см
Таким образом, длина биссектрисы равнобедренного треугольника с заданными сторонами составляет приблизительно 4.82 см.
Что такое биссектриса треугольника
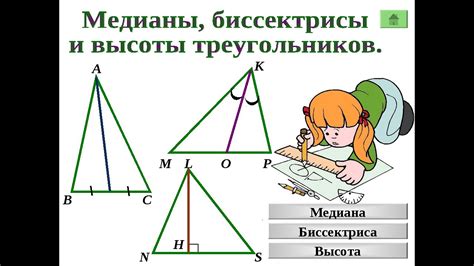
В равнобедренном треугольнике биссектриса делит основание треугольника на две равные отрезки. Основание равнобедренного треугольника - это сторона, противолежащая вершине, которая имеет двойную меру угла при этой вершине. Таким образом, биссектриса равнобедренного треугольника является высотой и медианой одновременно.
Для вычисления биссектрисы равнобедренного треугольника используется следующая формула:
Биссектриса = 2 / (2 + √(2)), где √ обозначает квадратный корень.
Найдем значение биссектрисы на примере равнобедренного треугольника ABC:
- Измерим длину основания треугольника AB и получим значение a.
- Вычислим биссектрису треугольника по формуле: Биссектриса = 2 / (2 + √(2)).
- Подставим значение a в формулу и получим конечный результат.
Формула для нахождения биссектрисы равнобедренного треугольника
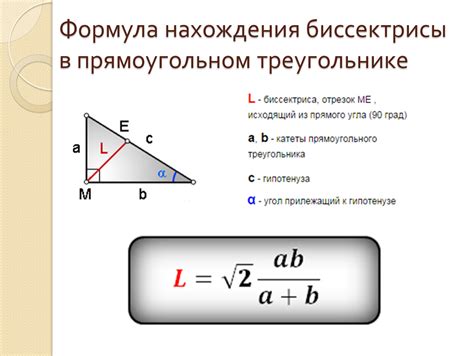
Для нахождения длины биссектрисы равнобедренного треугольника с известными длинами сторон можно использовать следующую формулу:
Длина биссектрисы = 2 * √(a * b * p * (p - c)) / (a + b),
где a и b - длины равных сторон, c - длина третьей стороны, а p - полупериметр треугольника.
Зная длины двух равных сторон и третьей стороны, вы можете подставить их в формулу и вычислить длину биссектрисы равнобедренного треугольника.
Пример:
Пусть в равнобедренном треугольнике известны длины равных сторон a = 4 см и третьей стороны c = 6 см. Найдем длину биссектрисы.
Сначала найдем полупериметр треугольника p:
p = (2a + c) / 2 = (2 * 4 + 6) / 2 = 14 / 2 = 7 см.
Теперь используем формулу:
Длина биссектрисы = 2 * √(4 * 6 * 7 * (7 - 6)) / (4 + 6) = 2 * √(168) / 10 ≈ 2 * 12.96 / 10 ≈ 1.73 см.
Таким образом, длина биссектрисы равнобедренного треугольника с равными сторонами 4 см и третьей стороной 6 см составляет около 1.73 см.
Пример решения задачи

Для начала, мы знаем, что биссектриса угла делит его на два равных угла. Так как треугольник ABC равнобедренный, у нас есть две равные стороны AB и AC, а значит, у нас есть два равных угла: угол ABC и угол ACB.
Мы можем найти биссектрису, используя формулу: BD = (2 * AB * AC * cos(A/2)) / (AB + AC), где AB и AC – длины сторон треугольника, а A – мера угла BAC.
Например, пусть AB = 8 и AC = 6, и угол BAC равен 60 градусам.
Подставим значения в формулу:
BD = (2 * 8 * 6 * cos(60/2)) / (8 + 6)
BD = (96 * cos(30)) / 14
Заметим, что cos(30) равен √3/2.
BD = (96 * √3/2) / 14
BD = (48√3) / 14
BD ≈ 6,77
Таким образом, биссектриса угла BAC (BD) в заданном равнобедренном треугольнике равна приблизительно 6,77.
Свойства биссектрисы равнобедренного треугольника
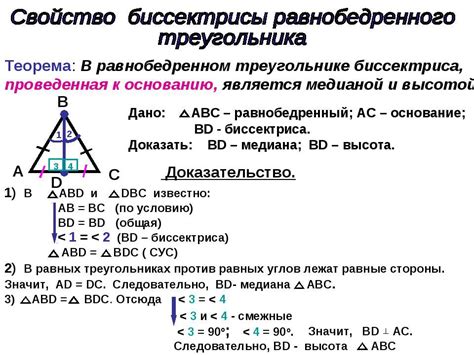
Свойства биссектрисы равнобедренного треугольника:
- Равные углы: Биссектриса делит угол треугольника на два равных угла, что делает ее очень полезным инструментом при нахождении углов равнобедренного треугольника.
- Свойства делящего отрезка: Биссектриса делит противоположную сторону треугольника на две части, пропорциональные смежным сторонам этого угла. Это значит, что отношение длины смежных сторон к длине противоположной стороны будет одинаковым.
- Высота и медиана: Биссектриса равнобедренного треугольника также является его высотой и медианой. Это означает, что она перпендикулярна основанию треугольника и делит его на две равные части.
- Центр вписанной окружности: Биссектриса равнобедренного треугольника является радиусом вписанной окружности, а точка их пересечения - центром этой окружности. Эта окружность проходит через вершины треугольника и касается всех его сторон.
Зная свойства биссектрисы равнобедренного треугольника, можно использовать их для нахождения углов и длин сторон. Это полезный инструмент для решения задач и построения треугольников.
Задачи с биссектрисами равнобедренных треугольников
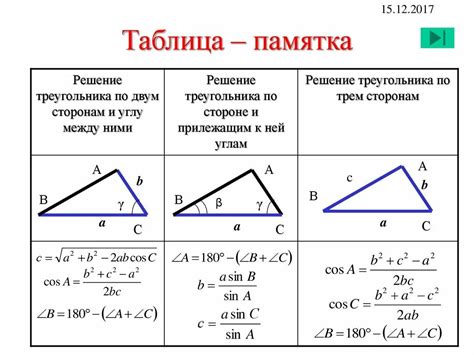
Ниже приведены некоторые типичные задачи, в которых используются биссектрисы равнобедренных треугольников:
| № | Задача | Решение |
|---|---|---|
| 1 | Найти длину биссектрисы | Используя формулу для длины биссектрисы равнобедренного треугольника: l = (2 * a * b * cos(α/2)) / (a + b), где l - длина биссектрисы, a и b - стороны треугольника, α - угол при основании, можно вычислить длину биссектрисы. |
| 2 | Найти площадь треугольника | Воспользовавшись формулой площади равнобедренного треугольника: S = (b * h) / 2, где S - площадь треугольника, b - длина основания, h - высота, можно вычислить площадь треугольника. |
| 3 | Найти угол при основании | Используя теорему косинусов для равнобедренного треугольника: a^2 = b^2 + b^2 - 2 * b * b * cos(α), где a и b - стороны треугольника, α - угол при основании, можно найти угол при основании. |
Это только несколько примеров задач, связанных с биссектрисами равнобедренных треугольников. Используя этих немного формулы и принципы, можно решать разнообразные геометрические задачи, связанные с равнобедренными треугольниками.