Равнобедренный треугольник - это треугольник, у которого две стороны равны между собой. Изучение свойств равнобедренных треугольников является важной частью геометрии, и одной из таких свойств является то, что биссектриса треугольника делит его угол на два равных угла.
Биссектриса - это линия, которая делит угол на два равных угла. В равнобедренном треугольнике каждый из двух оснований делит вершину (угол) на два равных угла. Для того чтобы найти биссектрису равнобедренного треугольника, необходимо знать длину одной из его сторон.
Существует несколько способов нахождения биссектрисы равнобедренного треугольника по стороне. Один из самых простых способов - использование теоремы синусов. Для этого необходимо найти длину биссектрисы с помощью формулы, в которую входят длина стороны треугольника и синус половины угла при основании треугольника.
Как найти биссектрису равнобедренного треугольника?

Биссектрисой равнобедренного треугольника называется отрезок, который делит угол на два равных по величине угла.
Для того чтобы найти биссектрису равнобедренного треугольника по стороне, нужно выполнить следующие шаги:
- Измерьте длину одной из сторон треугольника, которая является равной. Обозначим эту длину как a.
- Постройте перпендикуляр к стороне треугольника, проходящий через середину этой стороны.
- Измерьте длину построенного перпендикуляра и обозначим ее как b.
- Биссектриса будет равна половине разности длин стороны треугольника и построенного перпендикуляра: b/2 = (a-b)/2.
Теперь вы знаете, как найти биссектрису равнобедренного треугольника по стороне.
Математическое определение биссектрисы
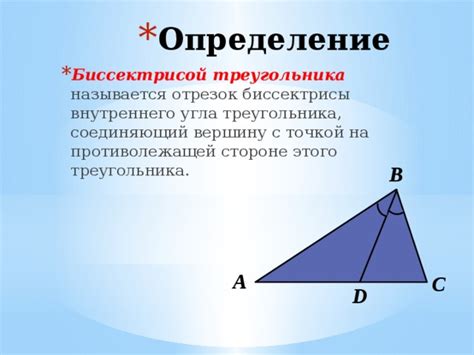
Для нахождения биссектрисы равнобедренного треугольника по стороне, нужно разделить эту сторону пополам и провести прямую через середину стороны и вершину треугольника. Узнать точку пересечения биссектрисы и основания треугольника поможет теорема о касательных, которая гласит, что биссектриса делит основание треугольника пропорционально отношению длины другой стороны к длине основания.
Математическое определение биссектрисы позволяет находить ее без использования специальных инструментов, а величина угла между биссектрисой и стороной равняется половине величины угла при вершине треугольника.
Алгоритм нахождения биссектрисы по стороне
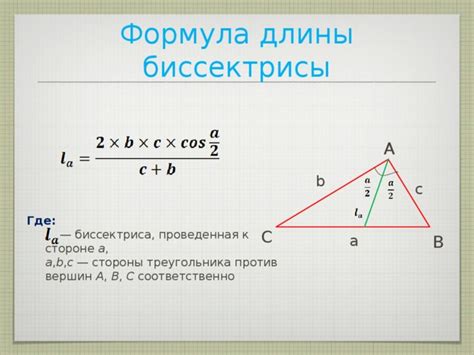
- Найдите половину длины стороны равнобедренного треугольника, для которой нужно найти биссектрису. Пусть это значение будет равно a.
- Используя теорему Пифагора, найдите длину основания треугольника. Для этого возьмите корень квадратный из разности квадрата половины стороны и квадрата радиуса вписанной окружности. Пусть это значение будет равно c.
- Основание треугольника - это одна из сторон, от которой нужно найти биссектрису. Разделите длину основания на 2, чтобы найти половину основания. Пусть это значение будет равно b.
- Косинус половины угла, через который проходит биссектриса, можно найти по формуле cos(угол/2) = b / c.
- Найденное значение косинуса половины угла используйте для вычисления самого угла с помощью функции arccos. Не забудьте перевести результат из радиан в градусы, если это требуется.
Теперь у вас есть значение угла и одна из его сторон. Используя эту информацию, вы можете построить биссектрису равнобедренного треугольника. Кроме того, с помощью этого алгоритма можно найти биссектрисы других типов треугольников, если известны соответствующие значения.