На уроках математики в 6 классе, ученики изучают различные аспекты десятичных дробей, включая нахождение их частей от заданного числа. На первый взгляд, задачи по нахождению части числа могут показаться сложными, но на самом деле существуют несколько простых способов решения таких задач.
Один из самых простых способов нахождения части числа - использование процентов. Предположим, что нужно найти 30% от числа 150. Для этого достаточно умножить число на процент и разделить результат на 100. В нашем примере, 30% от 150 будет равно (150 * 30) / 100 = 45.
Еще одним способом нахождения части числа является использование десятичных дробей. Для этого нужно просто разделить число на 100 и умножить результат на нужное количество процентов. Например, если нужно найти 40% от числа 250, то сначала нужно разделить 250 на 100, получив 2.5, а затем умножить результат на 40: 2.5 * 40 = 100.
Таким образом, нахождение части числа не является сложной задачей, если использовать соответствующие математические методы. Использование процентов и десятичных дробей позволяет легко и быстро рассчитывать нужные части чисел, что пригодится в реальной жизни и в дальнейшем обучении математике.
Основы десятичных дробей

Основной компонент десятичной дроби - это десятичная точка, которая разделяет целую и дробную части числа. Например, в числе 3.14, 3 - целая часть, а 14 - дробная часть.
Для расчета десятичной дроби в 6 классе используются различные методы, например, метод сокращения дробей или метод записи части числа в виде обыкновенной дроби.
Десятичные дроби имеют определенную последовательность цифр после десятичной точки. Например, число 0.25 имеет две цифры после точки. Эти цифры называются знаками десятичной дроби.
Как и обычные числа, десятичные дроби могут быть сравниваемыми, складываемыми, вычитаемыми и умножаемыми. Для этих операций используются определенные правила и алгоритмы, которые помогают упростить вычисления с десятичными дробями.
Понимание основ десятичных дробей является важным для понимания более сложных математических концепций и для успешного применения их в реальной жизни.
Расчет десятичной дроби путем деления

Процесс деления начинается с записи числа, которое нужно разделить, над чертой дроби. Затем над чертой записывается число, на которое нужно поделить, а под чертой – результат деления и остаток.
Для примера, давайте найдем десятичную дробь 2/5.
- Записываем 2 над чертой.
- Записываем 5 под чертой.
- Делим: 2 ÷ 5 = 0,4.
- Записываем 0,4 под чертой.
Таким образом, десятичная дробь 2/5 равна 0,4.
Когда нужно найти часть от числа, которое уже является десятичной дробью, процесс деления продолжается в том же формате. Например, чтобы найти часть от числа 0,6, мы можем разделить его на 10:
- Записываем 0,6 над чертой.
- Записываем 10 под чертой.
- Делим: 0,6 ÷ 10 = 0,06.
- Записываем 0,06 под чертой.
Таким образом, часть от числа 0,6 равна 0,06.
Используя этот метод деления, можно легко найти десятичные дроби и части от чисел, что может быть полезно при решении различных задач и в повседневной жизни.
Расчет десятичной дроби путем умножения

Для того чтобы найти часть от числа в виде десятичной дроби, нужно умножить число на десятичную дробь, которая представляет собой желаемую часть в десятичном виде.
Рассмотрим пример. Предположим, что нам нужно найти треть от числа 6.
| Шаг | Действие | Результат |
|---|---|---|
| 1 | Умножить число на десятичную дробь | 6 * 1/3 = 2 |
Таким образом, треть от числа 6 равна 2. Полученное значение соответствует десятичной дроби 0.66666...
Помните, что при умножении числа на десятичную дробь, можно получить точное десятичное значение только при условии, что десятичная дробь имеет конечное число цифр после запятой. Если число цифр после запятой бесконечно, то результат будет приближенным числом, и для получения точного значения могут потребоваться дополнительные шаги.
Расчет десятичной дроби путем сложения

В данном разделе мы рассмотрим способ расчета десятичной дроби путем сложения. Этот способ основан на разложении десятичной дроби на сумму десятичных дробей с единичными знаменателями.
При расчете десятичной дроби путем сложения необходимо следовать следующим шагам:
- Разложить исходное число на сумму десятичных дробей, где каждая дробь имеет знаменатель, равный 10, 100, 1000 и т. д., в зависимости от количества знаков после запятой.
- Выполнить сложение полученных дробей, при необходимости дополнив их нулями до одинакового количества знаков после запятой.
- Полученную сумму десятичных дробей привести к наименьшему знаменателю (в данном случае 10, так как исходное число было десятичной дробью).
- Упростить полученную дробь (при необходимости).
Например, для расчета части числа 3/5 методом сложения:
- Разложим число 3/5 на сумму десятичных дробей: 0.6 = 0.5 + 0.1.
- Сложим полученные дроби: 0.5 + 0.1 = 0.6.
- Приведем сумму к наименьшему знаменателю: 0.6 = 6/10.
- Упростим полученную дробь: 6/10 = 3/5.
Таким образом, часть числа 3/5, равная 0.6, можно получить путем сложения десятичных дробей с единичными знаменателями.
Расчет десятичной дроби путем вычитания
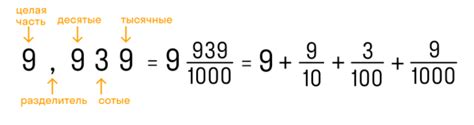
Для расчета десятичной дроби, необходимо выполнить следующие действия:
- Запишите число, от которого нужно найти часть, в десятичном виде. Например, если нужно найти часть числа 6, мы запишем его как 6,0.
- Запишите число, часть от которого нужно найти, также в десятичном виде. Например, если нужно найти две трети от числа 6, мы запишем его как 0,6666 (приближенно).
- Вычитайте второе число из первого, записывая результат каждого шага в таблицу. Начинайте с разряда равного единице, затем переходите к десяткам, сотым, тысячным и так далее.
- Продолжайте вычитать, пока не получите достаточно точный результат или не превысите заданную точность вычисления.
Например, если нужно найти две трети от числа 6, можно провести следующие вычисления:
| Шаг | Цифра разряда | Результат |
|---|---|---|
| 1 | 0,6666 | 6,0 - 0,6666 = 5,3334 |
| 2 | 0,0666 | 5,3334 - 0,0666 = 5,2668 |
| 3 | 0,0066 | 5,2668 - 0,0066 = 5,2602 |
Таким образом, две трети от числа 6 равны приближенно 5,2602.
Округление десятичных дробей
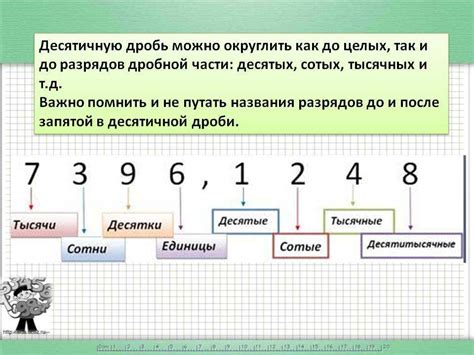
Существуют различные правила округления десятичных дробей, которые определяют, как число будет округлено. Наиболее распространенными являются следующие правила:
| Правило округления | Пример |
|---|---|
| Округление до ближайшего целого числа | Округление числа 5,6 даст 6, а числа 5,4 даст 5 |
| Округление до наименьшего целого числа (в меньшую сторону) | Округление числа 5,6 даст 5, а числа 5,4 даст 5 |
| Округление до наибольшего целого числа (в большую сторону) | Округление числа 5,6 даст 6, а числа 5,4 даст 6 |
| Округление до наибольшего целого числа (в большую сторону) | Округление числа 5,6 даст 6, а числа 5,4 даст 6 |
Выбор метода округления зависит от конкретной ситуации и требуемой точности результата. В некоторых случаях округление может привести к искажению данных, поэтому важно внимательно подходить к его применению.
Округление десятичных дробей широко используется в различных областях, включая экономику, финансы, статистику и программирование. Понимание правил округления поможет улучшить точность и надежность расчетов с использованием десятичных чисел.
Понятие и применение процента в десятичной форме

Для перевода процента в его десятичную форму необходимо разделить значение процента на 100. Например, если у нас есть процентное значение 25%, то его десятичная форма будет равна 0.25.
Процент в десятичной форме находит свое применение в различных математических операциях и задачах. Например, при умножении числа на процент, мы можем использовать его десятичную форму для более удобных расчетов. Кроме того, процент в десятичной форме может быть использован при решении задач на увеличение или уменьшение числа на определенный процент.
Также, процент в десятичной форме может быть полезен при сравнении или анализе различных данных. Например, при сравнении ставок процента по различным банковским вкладам, мы можем использовать десятичную форму для более точного и удобного сравнения.
Важно помнить, что процент в десятичной форме всегда находится в пределах от 0 до 1. Например, 50% в десятичной форме будет равно 0.5.
Использование процента в десятичной форме позволяет более точно и легко работать с долями и частями чисел в математических расчетах и задачах, что делает его важным инструментом для понимания и решения различных математических задач.
Практические примеры по расчету десятичных дробей

- Пример 1: Найдите 1/4 от числа 24.
- Пример 2: Найдите 3/5 от числа 35.
- Пример 3: Найдите 2/3 от числа 18.
Чтобы найти 1/4 от числа 24, нужно разделить 24 на 4: 24 ÷ 4 = 6. Таким образом, 1/4 от числа 24 равно 6.
Для нахождения 3/5 от числа 35 нужно умножить 35 на 3/5: 35 × 3/5 = 21. Таким образом, 3/5 от числа 35 равно 21.
Для нахождения 2/3 от числа 18 нужно умножить 18 на 2/3: 18 × 2/3 = 12. Таким образом, 2/3 от числа 18 равно 12.
Это всего лишь несколько примеров использования десятичных дробей для вычисления частей числа. Создание большего числа примеров позволит вам закрепить эти навыки и улучшить свое понимание дробей.