Для того чтобы рассчитать частоту, необходимо знать формулу, которая лежит в основе данной процедуры. Формула для вычисления частоты также позволяет определить относительную и накопленную частоту для каждого значения, что может быть полезным при сравнении различных выборок.
Приведем пример: допустим, у нас есть выборка, содержащая данные о предпочтениях людей в выборе книг. В этой выборке есть 100 человек, и мы хотим узнать, какие книги пользуются наибольшей популярностью. Для этого мы рассчитываем частоту каждой книги – сколько раз она упоминается в общей выборке из 100 человек.
Изучение частоты в статистике

Для определения частоты можно использовать различные методы, включая сбор и учет данных, построение таблиц и графиков. Частота может быть представлена числами или относительными значениями, которые показывают, сколько раз определенное значение встречается в наборе данных.
Изучение частоты позволяет выявить различные характеристики данных, такие как мода (наиболее часто встречающееся значение), медиана (значение, которое делит набор данных пополам), и среднее значение (сумма всех значений, деленная на их количество). Анализ частоты также может помочь определить выбросы или аномалии в данных.
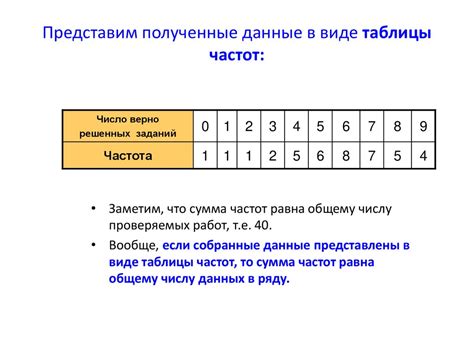
Частота может быть представлена в виде таблицы или графика. Таблица частот показывает количество раз, которое каждое значение встречается в наборе данных. График частоты позволяет визуализировать распределение данных и увидеть, какие значения встречаются чаще или реже.
Что такое частота и как она вычисляется?

Для вычисления частоты необходимо привести данные к удобному виду и подсчитать количество встречающихся значений или событий. Результат представляет собой количество, которое далее можно использовать для анализа данных и построения графиков.
Формула для вычисления частоты проста:
Частота = количество встречающихся значений / общее количество значений
Например, представим, что у нас есть выборка студентов с указанием их возраста:
18, 20, 22, 20, 19, 20, 21, 22, 18, 20
Чтобы вычислить частоту возрастов, сначала подсчитаем количество встречающихся значений:
Для возраста 18: 2
Для возраста 19: 1
Для возраста 20: 4
Для возраста 21: 1
Для возраста 22: 2
Теперь, используя формулу, мы можем вычислить частоту каждого возраста:
Частота 18 = 2 / 10 = 0.2 или 20%
Частота 19 = 1 / 10 = 0.1 или 10%
Частота 20 = 4 / 10 = 0.4 или 40%
Частота 21 = 1 / 10 = 0.1 или 10%
Частота 22 = 2 / 10 = 0.2 или 20%
Таким образом, мы определили частоту каждого возраста и можем использовать эту информацию для анализа данных и построения графиков, например, столбчатой диаграммы.
Вычисление частоты позволяет более полно представить статистическую информацию о данных и выявить закономерности и тенденции.
Примеры использования частоты в статистике
1. Исследование рынка:
При исследовании рынка частота может быть использована для определения доли рынка, занимаемой конкретным продуктом или брендом. Например, путем анализа частоты покупок или предпочтений потребителей, можно определить, какую долю рынка занимает определенный продукт или бренд.
2. Медицинские исследования:
В медицинских исследованиях частоту можно использовать для определения распространенности определенного заболевания или состояния. Например, путем анализа частоты появления определенных симптомов или диагнозов, можно определить, насколько часто встречается это заболевание в популяции.
3. Социологические исследования:
4. Финансовый анализ:
В финансовом анализе частоту можно использовать для анализа доходов или расходов компании. Например, путем анализа частоты появления определенных видов расходов или продаж, можно определить, какие элементы влияют на финансовое состояние предприятия.
Все эти примеры демонстрируют, как использование частоты может помочь в анализе и понимании различных ситуаций и явлений в статистическом анализе.