Описанная окружность - это окружность, которая проходит через вершины треугольника. Она является одной из основных геометрических фигур, которые рассматриваются в теории треугольников.
Равнобедренный треугольник - это треугольник, у которого две стороны равны друг другу. В таком треугольнике углы при основании также равны.
В данной статье мы рассмотрим алгоритм поиска центра описанной окружности равнобедренного треугольника. Зная длину стороны и основание треугольника, мы сможем точно определить ее местоположение на плоскости.
Итак, чтобы найти центр описанной окружности равнобедренного треугольника, нам понадобится вычислить координаты трех точек: вершины треугольника и его основания. Для этого можно воспользоваться формулами и свойствами равнобедренного треугольника, а также знаниями о координатной плоскости.
Описание проблемы

Равнобедренный треугольник имеет две равные стороны и два равных угла. Чтобы найти центр описанной окружности такого треугольника, используем два угла, базирующихся на равных сторонах.
Сначала проведем биссектрисы углов этого треугольника. Биссектриса - это линия, которая делит угол пополам.
Затем определим пересечение этих двух биссектрис - это и будет центр описанной окружности нашего равнобедренного треугольника.
Для наглядности и лучшего понимания процесса, представим себе, что у нас есть равнобедренный треугольник ABC с основанием AB и боковыми сторонами BC и AC. Мы хотим найти центр описанной окружности этого треугольника.
| Центр описанной окружности равнобедренного треугольника ABC |
A | | | |\ | \ | \ | \ | \ | \ | \ B-------C |
Что такое описанная окружность равнобедренного треугольника?
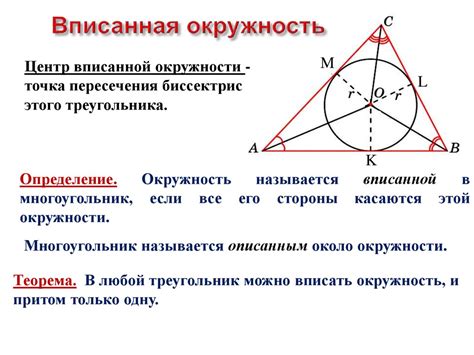
Равнобедренный треугольник имеет две равные стороны и соответствующие равные углы у основания. Описанная окружность равнобедренного треугольника имеет особое значение, так как она является важным геометрическим свойством и может использоваться для решения различных задач.
Центр описанной окружности равнобедренного треугольника лежит на перпендикулярной биссектрисе угла между равными сторонами треугольника. Эта биссектриса делит основание треугольника на две равные части и перпендикулярна ему. Центр окружности является серединой дуги основания, которая не включает вершину треугольника.
Описанная окружность равнобедренного треугольника имеет множество свойств и применений. Например, она может использоваться для нахождения биссектрисы угла или для определения достаточности условия равнобедренности треугольника. Кроме того, описанная окружность является важной составляющей различных геометрических конструкций и доказательств.
Нахождение центра описанной окружности
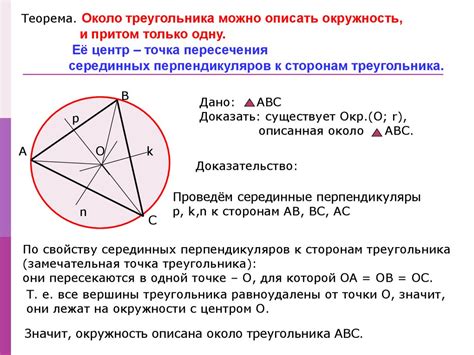
Центр описанной окружности равнобедренного треугольника может быть найден с помощью нескольких методов:
1. Использование перпендикуляра к основанию
Для нахождения центра описанной окружности равнобедренного треугольника можно построить перпендикуляр к одной из сторон, проходящий через середину основания треугольника. Точка пересечения этого перпендикуляра с высотой, проведенной из вершины до основания, будет являться центром описанной окружности.
2. Равенство угловых мер
Другим способом нахождения центра описанной окружности является проверка равенства угловых мер двух углов треугольника, образованных стороной, содержащей высоту. Если эти углы равны, то точка пересечения высоты и серединной перпендикуляра, проведенного к стороне, будет центром окружности.
3. Использование радиуса и середины стороны
Третий способ заключается в построении окружности с радиусом, равным половине длины стороны треугольника, и центром в середине этой стороны. Точка пересечения этой окружности с высотой, проведенной из вершины до основания, будет центром описанной окружности.
С использованием одного из этих методов можно найти центр описанной окружности равнобедренного треугольника. Этот центр является важным понятием при изучении геометрии и может быть использован для решения различных задач и доказательств.
Метод 1: Определение центра с помощью перпендикуляров

| 1. | Проведите биссектрисы двух углов треугольника, которые прилегают к основанию. |
| 2. | На пересечении биссектрис найдите точку O - центр окружности. |
Таким образом, нахождение центра описанной окружности равнобедренного треугольника с помощью перпендикуляров является простым и эффективным методом.
Метод 2: Определение центра с помощью середин сторон
Существует второй метод определения центра описанной окружности равнобедренного треугольника с помощью середин сторон.
Для этого нужно найти середину каждой стороны треугольника. Середина стороны – это точка, которая делит сторону пополам.
Затем, соединяем середины двух сторон равнобедренного треугольника. Получаем отрезок, который является диаметром описанной окружности.
Центр описанной окружности находится на пересечении двух середин сторон треугольника.
Применим этот метод на примере:
Пусть у нас имеется равнобедренный треугольник ABC, где AB = AC.
Найдем середины сторон AB и AC, обозначим их как M и N соответственно.
Теперь соединим точки M и N. Получим отрезок MN, который является диаметром описанной окружности.
Проведем перпендикуляр к отрезку MN из середины стороны AB. Пусть перпендикуляр пересекается с отрезком MN в точке O. Тогда точка O является центром описанной окружности равнобедренного треугольника ABC.
Таким образом, второй метод позволяет определить центр описанной окружности равнобедренного треугольника с помощью середин сторон.
Примеры решений
Приведем несколько примеров решения задачи о нахождении центра описанной окружности равнобедренного треугольника.
| Пример 1 | Пример 2 |
|---|---|
Дано: равнобедренный треугольник ABC с основанием AB и боковой стороной AC. Решение: 1. Найдем середину основания треугольника M. 2. Найдем середину боковой стороны треугольника N. 3. Проведем прямую, проходящую через точки M и N. 4. Центр описанной окружности равнобедренного треугольника находится на пересечении этой прямой и высоты треугольника. | Дано: равнобедренный треугольник XYZ с основанием YZ и боковой стороной YX. Решение: 1. Найдем середину основания треугольника P. 2. Найдем середину боковой стороны треугольника Q. 3. Проведем прямую, проходящую через точки P и Q. 4. Центр описанной окружности равнобедренного треугольника находится на пересечении этой прямой и высоты треугольника. |
Таким образом, центр описанной окружности равнобедренного треугольника можно найти с помощью проведения прямой через середины основания и боковой стороны треугольника. Пересечение этой прямой с высотой треугольника дает искомую точку - центр окружности.
Пример 1: Равнобедренный треугольник с заданными координатами
Предположим, у нас имеются заданные координаты вершин равнобедренного треугольника. Для нахождения центра описанной окружности нам необходимо выполнить следующие шаги:
1. Найдем середину основания треугольника. Для этого можно использовать формулу нахождения средней точки между двуми точками:
x = (x1 + x2) / 2 y = (y1 + y2) / 2Где (x1, y1) и (x2, y2) - координаты вершин основания треугольника.
2. Найдем длину боковой стороны треугольника. Для этого можно использовать формулу нахождения расстояния между двумя точками:
a = √((x2 - x1)^2 + (y2 - y1)^2)Где (x1, y1) и (x2, y2) - координаты вершин основания треугольника.
3. Найдем высоту треугольника. Для равнобедренного треугольника, высота будет перпендикулярна основанию и проходить через его середину. Зная длину боковой стороны (a) и координаты середины основания (x, y), мы можем найти координаты вершины треугольника:
x3 = x y3 = y + a * (sqrt(3) / 2)4. Найдем центр описанной окружности, который будет находиться на пересечении медиан треугольника. Медианы треугольника - это отрезки, соединяющие вершины треугольника с серединой противоположной стороны. Найдем середины оставшихся двух сторон треугольника:
x4 = (x2 + x3) / 2 y4 = (y2 + y3) / 2 x5 = (x1 + x3) / 2 y5 = (y1 + y3) / 25. Используя полученные координаты вершин треугольника, мы можем найти координаты центра описанной окружности как точку пересечения медиан треугольника. Для этого можно использовать следующую формулу:
x_center = ((y5 - y4) * x + (x4 - x5) * x1 + (y4 * x5 - y5 * x4)) / ((y5 - y4) + (y4 - y5)) y_center = ((y4 - y5) * y + (x5 - x4) * y1 + (x4 * y5 - x5 * y4)) / ((x5 - x4) + (x4 - x5))Теперь мы можем использовать найденные значения для дальнейших вычислений или визуализации равнобедренного треугольника и его описанной окружности.