Центральный угол – одно из основных понятий геометрии, которое широко используется при изучении свойств окружностей. Этот угол образуется двумя радиусами, проведенными к концам дуги окружности. Знание центрального угла позволяет определить много полезных параметров и свойств окружности.
Если известен радиус окружности, найти ее центральный угол – нетрудная задача. Для этого необходимо знать, как узнать длину дуги окружности с известным радиусом. Дуга строится на основе центрального угла, измеряемого в радианах или в градусах. Зная радиус окружности и длину дуги, можно вычислить значение центрального угла с помощью специальной формулы.
В этой статье мы рассмотрим подробное руководство по нахождению центрального угла окружности с известным радиусом. Это будет полезно для тех, кто интересуется геометрией и хочет более глубоко разобраться в свойствах окружностей.
Изучите определение и свойства центрального угла
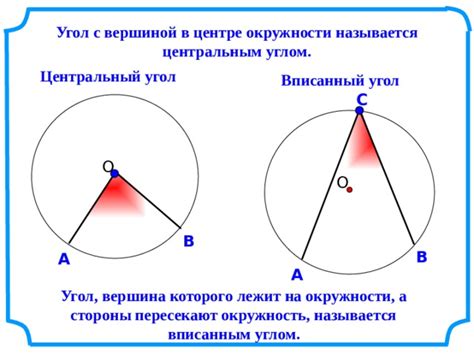
Основные свойства центрального угла:
1. Мера центрального угла равна длине дуги, заключенной между сторонами угла, разделенной радиусом окружности.
2. Все центральные углы, опирающиеся на одну и ту же дугу, равны между собой.
3. Центральный угол, опирающийся на дугу длиной в половину окружности (180 градусов или π радиан), называется прямым углом.
4. Сумма мер двух центральных углов, опирающихся на пересекающиеся дуги, равна 360 градусов или 2π радианам.
Изучение определения и свойств центрального угла поможет вам лучше понять его значение и его роль в геометрии окружностей. Выполняя задачи, связанные с центральными углами, вы сможете находить нужные измерения и совершать точные расчеты в соответствии с заданными условиями.
Определите значение радиуса окружности
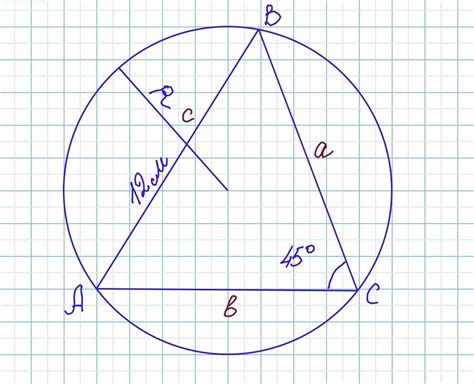
Если вам известны значения хотя бы одной её характеристики, можно определить радиус окружности. Характеристиками окружности могут быть её диаметр, длина окружности, площадь или центральный угол.
Если известен диаметр окружности, можно найти радиус, разделив его значение на 2.
Для определения радиуса по длине окружности необходимо длину разделить на 2π (пи), так как длина окружности равна произведению радиуса на 2π.
Если известна площадь окружности, радиус можно найти, взяв квадратный корень из отношения площади к π (пи).
Также радиус окружности можно найти, если известно значение центрального угла. Для этого необходимо узнать долю от 360°, соответствующую данному центральному углу, и умножить радиус на эту долю.
Приведённая таблица содержит формулы и примеры для вычисления радиуса окружности по различным характеристикам:
| Характеристика окружности | Формула | Пример |
|---|---|---|
| Диаметр | Радиус = Диаметр / 2 | Диаметр = 10 Радиус = 10 / 2 = 5 |
| Длина окружности | Радиус = Длина / (2π) | Длина = 20π Радиус = 20π / (2π) = 10 |
| Площадь | Радиус = √(Площадь / π) | Площадь = 25π Радиус = √(25π / π) = √25 = 5 |
| Центральный угол | Радиус = Радиус * (Угол / 360°) | Радиус = 8 Угол = 45° Радиус = 8 * (45 / 360) = 8 * 0.125 = 1 |
Сформулируйте задачу на поиск центрального угла

Для решения задачи по поиску центрального угла необходимо знать радиус окружности и понимать, как определить величину угла с использованием этой информации. При решении данной задачи помогут знания о геометрии окружностей и их свойствах.
Задача на поиск центрального угла может включать следующие элементы:
- Известный радиус окружности.
- Углы между радиусами, которые необходимо найти.
- Координаты точек на окружности, между которыми требуется найти угол.
- Дополнительные условия, такие как сектор окружности, определенный центральным углом, или условия совместности углов.
В зависимости от поставленной задачи, можно использовать различные методы для нахождения центрального угла. Например, можно использовать теорему о центральном угле или свойства треугольников, образуемых радиусами и стороной окружности.
Решение задачи на поиск центрального угла позволяет определить величину угла между заданными точками на окружности или углы между различными радиусами. Это может быть полезно при решении задач, связанных с геометрией, физикой, а также в других областях, где применяются знания о геометрии окружностей.
Примените формулу для расчета центрального угла

Для вычисления центрального угла окружности с известным радиусом существует специальная формула. Эта формула позволяет определить величину угла, который соответствует дуге окружности, если известен радиус окружности.
Формула для расчета центрального угла выглядит следующим образом:
Центральный угол = (Дуга / Радиус) * 180 / π
Где:
- Центральный угол - величина угла, выраженная в градусах;
- Дуга - длина дуги окружности, для которой требуется найти центральный угол;
- Радиус - радиус окружности;
- π - математическая константа, равная приблизительно 3.14159.
Используя эту формулу, вы можете легко рассчитать центральный угол окружности, зная значение дуги и радиуса. Это может быть полезно, например, при построении диаграмм или графиков, где требуется отобразить определенную часть окружности.
Выполните расчет центрального угла путем деления длины дуги на радиус
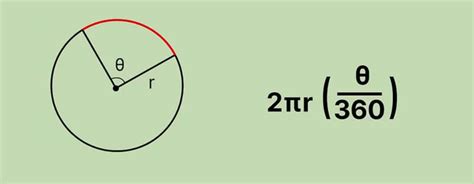
Чтобы найти центральный угол окружности с известным радиусом, вам необходимо выполнить простой расчет. Предположим, что у вас есть окружность с радиусом R и дугой, длина которой равна L.
В данном случае центральный угол может быть найден путем деления длины дуги на радиус:
Центральный угол = Длина дуги / Радиус
Для выполнения этого расчета следуйте следующим шагам:
- Определите длину дуги окружности, которую вы хотите измерить. Вы можете использовать формулу для расчета длины дуги окружности:
- Выразите центральный угол в радианах. Это можно сделать с помощью формулы:
- Подставьте известные значения в формулу и выполните расчет.
Длина дуги = Центральный угол (в радианах) * Радиус
Центральный угол (в радианах) = Длина дуги / Радиус
Расчет центрального угла путем деления длины дуги на радиус дает вам точное значение угла. Этот метод часто используется для измерения и построения окружностей в геометрии и инженерии.
Запишите полученное значение центрального угла
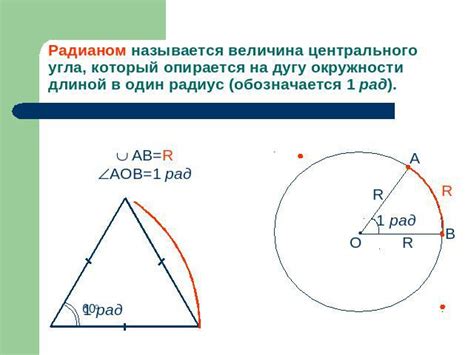
Полученное значение центрального угла окружности с известным радиусом можно запомнить для дальнейшего использования в вычислениях. Оно представляет собой значение угла в радианах, обозначаемое греческой буквой "фи" (φ).
Пример:
Если радиус окружности равен 5 сантиметрам, то центральный угол будет вычислен следующим образом:
φ = (длина дуги / радиус) = (5см / 5см) = 1 радиан
Таким образом, полученное значение центрального угла равно 1 радиану.
Запомните это значение, чтобы использовать его в дальнейших вычислениях или анализе задач, связанных с окружностями.
Приведите примеры решения задачи по нахождению центрального угла
Для нахождения центрального угла окружности с известным радиусом можно использовать формулу:
Центральный угол = (Длина дуги / Длина окружности) * 360
Приведем пример:
Пусть у нас есть окружность с радиусом 5 см. Нам нужно найти центральный угол для дуги длиной 10 см.
Сначала найдем длину окружности:
Длина окружности = 2 * π * радиус
Длина окружности = 2 * 3.14 * 5 см
Длина окружности = 31.4 см
Теперь, чтобы найти центральный угол, используем формулу:
Центральный угол = (10 см / 31.4 см) * 360
Центральный угол ≈ 114.65 градусов
Таким образом, для данного примера центральный угол окружности с радиусом 5 см при длине дуги 10 см равен примерно 114.65 градусам.