Центральный угол – это угол, вершина которого находится в центре окружности, а стороны проходят через две точки на окружности.
Центральные углы играют важную роль в геометрии и имеют множество применений. Они помогают в вычислении длин дуг и длин радиусов, а также в определении доли окружности, на которую проецируется данный угол.
Для того чтобы найти центральный угол, необходимо измерить его в градусах или радианах. Градусная мера центрального угла определяется как отношение его дуги к длине окружности, умноженное на 360. Радианная мера центрального угла вычисляется как отношение его дуги к радиусу окружности.
Примечание: Центральный угол всегда равен половине соответствующего междуцентрального угла.
Теперь, когда вы знаете, как найти центральный угол и его меру, вы можете использовать эти знания для решения различных задач в геометрии и математике. Успехов в изучении и применении центральных углов!
Определение центрального угла
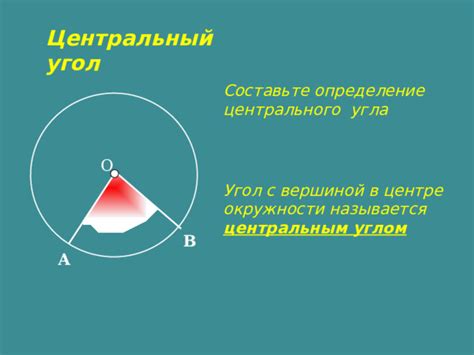
Для определения центрального угла необходимо знать длину дуги, ограничивающей этот угол, а также радиус окружности. Формула для вычисления центрального угла выглядит следующим образом:
| Формула: | угол = длина дуги / радиус окружности |
В данной формуле угол измеряется в радианах. Если требуется выразить угол в градусах, его значение необходимо умножить на 180 и поделить на число Пи (π).
Определение центрального угла является важной задачей в геометрии и находит применение в различных областях, таких как строительство, архитектура, компьютерная графика и другие.
Правила нахождения центрального угла
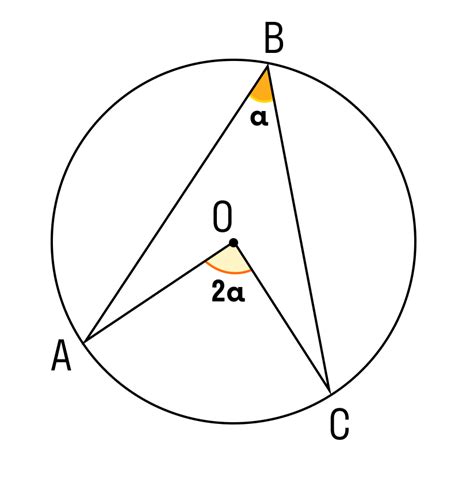
Для определения центрального угла необходимо знать его вершину (центр окружности) и две точки на окружности, через которые проходят стороны угла.
Правила нахождения центрального угла следующие:
| Пункт | Действие |
|---|---|
| 1 | Прокладывание линии из центра окружности к одной из точек на окружности, через которые проходит сторона угла. |
| 2 | Прокладывание линии из центра окружности к другой точке на окружности, через которую проходит другая сторона угла. |
| 3 | Измерение угла между прокладываемыми линиями. |
| 4 | Получение значения угла и его использование в дальнейших расчетах или задачах. |
Зная правила нахождения центрального угла, можно легко определить его величину и использовать эту информацию для решения задач различной сложности.
Применение центрального угла
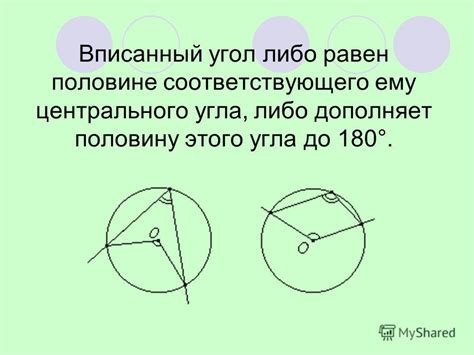
Центральный угол имеет широкое применение в геометрии и решении различных задач.
Одним из основных применений центрального угла является вычисление длины дуги окружности. Для этого необходимо знать величину центрального угла и радиус окружности. С помощью соответствующей формулы можно вычислить длину дуги и использовать ее в задачах, связанных с окружностями.
Центральный угол также применяется при решении задач на нахождение площади сектора окружности, которая представляет собой часть площади всей окружности, ограниченную двумя радиусами и дугой окружности. Формула для вычисления площади сектора включает в себя величину центрального угла и площадь всей окружности.
Другим применением центрального угла является нахождение дополнительного угла. Дополнительный угол к центральному углу на одной дуге окружности имеет размер, равный разности 360 градусов и угла на дуге. Это свойство можно использовать при решении геометрических задач, связанных с определением дополнительного угла.
Таким образом, центральный угол является важным понятием в геометрии и находит применение в решении различных задач, связанных с окружностями.
Примеры центральных углов в ежедневной жизни
Центральные углы встречаются в различных ситуациях на протяжении нашего обычного дня. Вот несколько примеров, где можно встретить центральные углы и применить знания о них:
1. Секундомер
У секундомера есть маленькая стрелка, которая движется вокруг диска с делениями. Когда стрелка совершает полный оборот и возвращается в исходное положение, она описывает центральный угол в 360 градусов.
2. Рулетка
Рулетка - это инструмент для измерения расстояний. При ее использовании можно увидеть, что полный оборот стрелки на рулетке составляет 360 градусов, что является центральным углом.
3. Календарь
На календаре мы видим разметку вокруг циферблата, которая описывает центральный угол. Когда стрелка указывает на определенную дату, эта разметка показывает угол, который она образует с нулевым положением.
4. Бумажное круговоротное меню
Во многих ресторанах и кафе используются круговоротные меню, которые позволяют выбрать блюда, поворачивая стрелку. Эта стрелка описывает центральный угол и помогает нам сделать выбор.
Знание о центральных углах может быть полезно во многих сферах нашей жизни. Используйте эти примеры, чтобы лучше понять и применить это понятие в практике.