Центроид - это особая точка, которая является средним положением всех точек фигуры, взвешенных по массе. Нахождение центроида сложной фигуры может быть непростой задачей, особенно когда форма фигуры нестандартная или имеет сложную геометрию. Однако, с помощью определенных методов и формул, вы сможете рассчитать центроид любой фигуры точно и эффективно.
Для начала, вам необходимо разбить сложную геометрическую фигуру на простые части, такие как треугольники, прямоугольники или круги. Затем, для каждой простой части, вы можете использовать известные формулы для нахождения центра масс. Например, для треугольника центр масс находится на пересечении медиан, а для круга - в его центре.
После того, как вы найдете центры масс для каждой простой части, вы можете рассчитать общий центроид сложной фигуры, используя формулу средневзвешенного. При этом, каждый центр масс умножается на массу соответствующей простой части, а затем суммируется и делится на общую массу.
Что такое центроид и почему он важен

Центроид важен, потому что он позволяет определить центральную точку фигуры и использовать ее во многих практических приложениях. Например, центроид можно использовать для нахождения центра тяжести фигуры, определения равновесных условий или расчета силы трения. Также центроид может быть использован для устранения неравномерной нагрузки или балансировки фигуры.
Для вычисления центроида сложной фигуры, нужно знать координаты всех ее точек. Затем необходимо выполнить определенные вычисления, чтобы получить средние значения координат x и y. Это можно сделать с использованием формулы для вычисления арифметического среднего каждой координаты.
Центроид является мощным инструментом для анализа и расчета различных параметров сложных фигур. Поэтому понимание того, что такое центроид и как его найти, является важным в широком спектре научных и практических областей.
Метод вычисления координат центроида
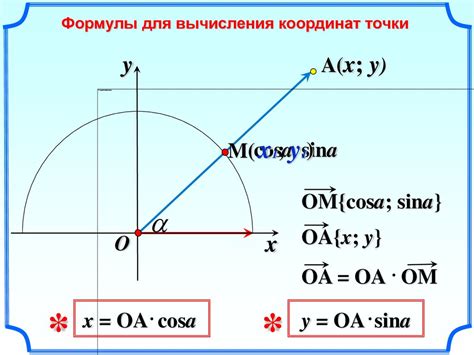
Центроид сложной фигуры может быть найден с помощью метода разделения площади на маленькие элементы и вычисления их геометрических характеристик. Этот метод основан на принципе, что площадь центроида всегда равна сумме площадей отдельных элементов, умноженных на их соответствующие координаты.
Для начала, фигура должна быть разбита на маленькие элементы, такие как треугольники, прямоугольники или квадраты. Каждый элемент должен иметь известные координаты вершин и площадь.
После этого, для каждого элемента вычисляются его координаты центра масс, используя формулу:
x = (x1 + x2 + x3) / 3
y = (y1 + y2 + y3) / 3
где (x1, y1), (x2, y2) и (x3, y3) - координаты вершин элемента.
Затем, площадь каждого элемента умножается на его соответствующие координаты центра масс, и эти значения суммируются. Общая площадь всех элементов также вычисляется и используется для нормализации координат центра масс, чтобы получить итоговые координаты центроида.
Окончательные координаты центроида вычисляются следующим образом:
x = sum(площадь * xцм) / общая площадь
y = sum(площадь * yцм) / общая площадь
где sum(площадь * xцм) и sum(площадь * yцм) - сумма площадей, умноженных на соответствующие координаты центра масс каждого элемента, а общая площадь - сумма площадей всех элементов.
Таким образом, метод вычисления координат центроида позволяет найти точку, которая является центром масс или "средним" положением всей сложной фигуры. Эта точка может быть полезна при анализе и моделировании различных систем.
Шаги для нахождения центроида
Начните с определения геометрической формы и размеров сложной фигуры. Убедитесь, что вы имеете все необходимые измерения, такие как длина, ширина и высота.
1. Разбейте фигуру на более простые геометрические формы, такие как прямоугольники, круги или треугольники. Это позволит вам легче вычислить центроид каждой отдельной части.
2. Постройте таблицу, где каждому участку фигуры будет соответствовать строка. В первом столбце укажите тип фигуры (например, прямоугольник или круг), во втором - его размеры.
| Тип фигуры | Размеры |
|---|---|
| Прямоугольник | Длина: 10, Ширина: 5, Высота: 3 |
| Круг | Радиус: 8 |
3. Для каждой фигуры вычислите ее площадь и координаты центра масс.
4. После того, как вы вычислите площади и координаты центров масс для каждой фигуры, объедините их, чтобы найти общий центроид сложной фигуры.
5. Проверьте свои вычисления, используя геометрическую формулу для центроида. Убедитесь, что координаты, полученные вами, правильно соответствуют формуле.
6. Проверьте результаты, используя графические программы или специальные онлайн-калькуляторы. Это поможет убедиться в правильности вычислений и найти возможные ошибки.
Следуя этим шагам, вы сможете успешно найти центроид сложной фигуры и использовать его для решения различных геометрических задач.
Пример 1: Нахождение центроида треугольника

Для нахождения центроида треугольника нужно узнать координаты вершин. Допустим, у нас есть треугольник с вершинами A(x1, y1), B(x2, y2) и C(x3, y3).
Шаг 1: Найти сумму координат X вершин треугольника и разделить ее на количество вершин, чтобы найти среднее значение координаты X центроида.
Шаг 2: Найти сумму координат Y вершин треугольника и разделить ее на количество вершин, чтобы найти среднее значение координаты Y центроида.
Шаг 3: Построить таблицу, где в первом столбце будут записаны координаты X вершин, а во втором столбце - координаты Y вершин.
| Вершина | X | Y |
|---|---|---|
| A | x1 | y1 |
| B | x2 | y2 |
| C | x3 | y3 |
Шаг 4: Вычислить среднее значение координаты X центроида и записать его в таблицу.
Шаг 5: Вычислить среднее значение координаты Y центроида и записать его в таблицу.
Таким образом, мы можем вычислить координаты центроида треугольника.
Пример 2: Нахождение центроида многоугольника
Для нахождения центроида многоугольника необходимо сначала найти сумму координат всех вершин многоугольника по оси X и по оси Y. Затем, найденные суммы нужно разделить на количество вершин многоугольника.
Возьмем в качестве примера многоугольник со следующими координатами вершин:
(2, 1), (4, 3), (6, 1), (4, -1)
Найдем суммы координат:
Сумма координат по оси X: 2 + 4 + 6 + 4 = 16
Сумма координат по оси Y: 1 + 3 + 1 + (-1) = 4
Теперь найдем центроид, разделив суммы координат на количество вершин, то есть на 4:
Координата центроида по оси X: 16 / 4 = 4
Координата центроида по оси Y: 4 / 4 = 1
Таким образом, центроид многоугольника с указанными координатами вершин будет находиться в точке (4, 1).
Этот метод можно применять для многоугольников любой формы и размера. Он позволяет найти точку, которая является центром тяжести фигуры и равномерно распределяет ее массу.