Расчет процентов от числа является одной из основных арифметических операций, которая находит применение во многих сферах жизни. Знание этой формулы позволяет рассчитать, например, скидки и наценки, процентную ставку, прибыльность инвестиций и многое другое.
Основной формулой для нахождения числа по процентам является уравнение, которое позволяет расчитать отношение процента к числу. Для этого необходимо умножить число на долю процента, выраженную в десятичных долях. Рассчитывая процентную ставку, необходимо разделить полученное значение на 100.
Например, если нам известно, что 20% от числа равно 40, мы можем использовать формулу и прийти к решению. Подставив значения в уравнение, мы получим: число = 40 / (20 / 100) = 40 / 0.20 = 200. Таким образом, число равно 200.
Проценты и числа: основные понятия

Число, к которому применяется процент, называется основой. Основа может быть любым числом, а процент - это отношение между основой и некоторым числом, выраженное в сотых долях.
Для вычисления числа по процентам используется простая формула:
| Формула | Описание |
|---|---|
| число = основа * (процент / 100) | Вычисляет число по процентам. |
Например, чтобы найти 15% от числа 200, нужно умножить 200 на (15 / 100), что равно 30. Таким образом, 15% от числа 200 равно 30.
Проценты могут использоваться для различных целей, например, для вычисления скидки, налога, прибыли и других значений. Они также помогают сравнивать числа и оценивать изменения величин.
Знание основных понятий и формул позволяет более эффективно работать с процентами и числами, а также решать различные задачи, связанные с вычислением процентов.
Что такое проценты? Что такое числа?

Процент представляет собой долю или часть числа, выраженную в сотых долях. Он обозначается знаком % и часто используется для описания отношения или изменения одной величины к другой. Например, если мы говорим о процентах, мы говорим о том, сколько частей от всего имеется или занимает какая-то величина. Проценты могут быть положительными или отрицательными числами.
Число, с другой стороны, это абстрактная математическая концепция, которая используется для представления количества или значения. Оно может быть представлено цифрами и используется для измерения и сравнения различных величин. Числа могут быть целыми или десятичными, положительными или отрицательными.
Проценты и числа взаимосвязаны и часто используются вместе для решения различных задач и вычислений. Например, проценты могут использоваться для вычисления скидок, налогов, процентного прироста или убытка и многого другого.
- Проценты представляют собой долю или часть числа, выраженную в сотых долях.
- Число – абстрактная математическая концепция, используемая для представления количества или значения.
- Проценты и числа взаимосвязаны и часто используются вместе для решения различных задач и вычислений.
Как найти число по процентам

Чтобы найти число по процентам, нужно умножить изначальное число на процентное соотношение и разделить на 100.
Формула для расчета:
Искомое число = Изначальное число * Процентное соотношение / 100
Например:
- Допустим, у нас есть число 200 и мы хотим найти 20% от него.
- Умножаем 200 на 20: 200 * 20 = 4000.
- Делим полученное значение на 100: 4000 / 100 = 40.
- Итак, 20% от числа 200 равно 40.
Таким образом, найти число по процентам достаточно просто, если знать формулу и следовать указанным шагам.
Что такое формула для нахождения числа по процентам?
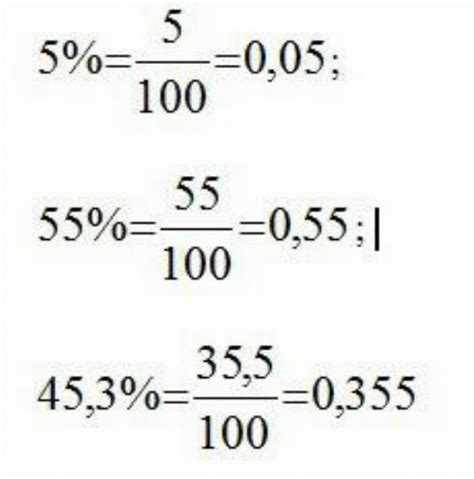
В основе формулы лежит понятие процента, который представляет собой долю от целого числа. Данный процент можно выразить в виде десятичной дроби или разделительной дроби.
Формула для нахождения числа по процентам имеет следующий вид:
Число = (Процент / 100) * Значение
Где:
- Число - искомое значение числа;
- Процент - значение процента;
- Значение - число, от которого берется процент.
Эта формула позволяет легко и быстро вычислить число по заданному проценту. Например, если нужно найти 20% от числа 100, то применяя данную формулу можно получить результат:
Число = (20 / 100) * 100 = 20
Таким образом, 20% от числа 100 равно 20.
Формула для нахождения числа по процентам является важным инструментом в финансовой сфере, торговле и других сферах деятельности, где необходимо расчетное значение числа на основе заданного процента.
Примеры расчетов чисел по процентам
Рассмотрим несколько примеров, чтобы понять, как использовать формулу для нахождения числа по процентам.
Пример 1:
Допустим, у вас есть число 150 и вы хотите найти 25% от этого числа. Для этого применяем формулу:
число * (процент / 100) = результат
Подставляем значения:
150 * (25 / 100) = 37.5
Ответ: 37.5. Таким образом, 25% от числа 150 равно 37.5.
Пример 2:
Допустим, у вас есть число 200 и вы хотите найти 70% от этого числа. Используем формулу:
число * (процент / 100) = результат
Подставляем значения:
200 * (70 / 100) = 140
Ответ: 140. Таким образом, 70% от числа 200 равно 140.
Пример 3:
Предположим, у вас есть число 80 и вы хотите найти 15% от этого числа. Применяем формулу:
число * (процент / 100) = результат
Подставляем значения:
80 * (15 / 100) = 12
Ответ: 12. Таким образом, 15% от числа 80 равно 12.
Используя эти примеры, вы можете легко рассчитывать проценты от чисел, применяя соответствующую формулу. Запомните ее и используйте в своих расчетах!
Проценты и числа: практическое применение

Проценты могут быть использованы при расчете скидок и наценок в торговле. Например, при покупке товара со скидкой в 30%, нужно умножить его стоимость на 0,7 (100% - 30% = 70%). А если требуется установить наценку, например, в 20%, нужно умножить стоимость товара на 1,2 (100% + 20% = 120%).
Также проценты часто используются при расчете процентного соотношения. Например, при анализе результатов опроса, можно вычислить, какой процент опрошенных дали тот или иной ответ. Это помогает понять, насколько распространено то или иное мнение среди опрошенных.
В финансовой сфере проценты играют особую роль. Они используются при расчете процентных ставок по кредитам и вкладам, при определении процентной составляющей выплат по ипотеке и другим финансовым операциям.
Расчет процентов также применяется в математических задачах. Например, при решении задач на увеличение или уменьшение числа на определенный процент, нужно умножить число на 1 плюс (или минус) процентное отношение. Эта формула может быть использована для решения задач различной сложности.
В образовательной сфере проценты используются при оценке успеваемости студентов и определении процента правильных ответов при тестировании.
Таким образом, проценты и числа тесно связаны в различных сферах деятельности. Понимание процентов и умение работать с ними позволяет легко выполнять расчеты, делать анализ данных и принимать различные финансовые решения.
Применение расчетов чисел по процентам в финансах

Применение расчетов чисел по процентам в финансах может быть очень разнообразным. Например, при планировании инвестиций в акции или облигации, нужно учитывать процентный доход или доходность по инструменту, чтобы рассчитать ожидаемую прибыль.
Другой пример - кредитование. Чтобы определить стоимость кредита, необходимо знать процентную ставку, которую будет взимать банк. С помощью расчетов по процентам можно определить ежемесячные платежи и суммарную стоимость кредита.
Также расчеты по процентам важны для определения инфляции и роста цен на товары. Например, с помощью процентных расчетов можно определить, на сколько увеличится стоимость продуктов питания в следующем году, если инфляция составит определенный процент.
В целом, знание и умение применять расчеты чисел по процентам является фундаментальным для финансового анализа и планирования. Они позволяют принимать взвешенные финансовые решения и учитывать влияние процентов на финансовые параметры и результаты деятельности.
Другие примеры использования расчета чисел по процентам

Расчет чисел по процентам очень полезен во многих ситуациях и может быть применен в различных областях.
Например, в банковской сфере расчет чисел по процентам может использоваться для определения ежемесячного платежа по кредиту или расчета процентной ставки на вкладе. Если известны сумма кредита, срок и процентная ставка, можно легко вычислить размер ежемесячного платежа. А если известна сумма вклада и процентная ставка, можно определить, какая сумма будет на вкладе через определенное количество лет.
В розничной торговле расчет чисел по процентам может использоваться для определения скидки на товар. Например, если известна стоимость товара и процент скидки, можно легко вычислить сумму скидки и итоговую стоимость товара.
В сфере инвестиций расчет чисел по процентам может использоваться для определения доходности инвестиции. Если известна сумма инвестиции, процент доходности и срок инвестиции, можно легко вычислить итоговую сумму дохода.
| Пример | Расчет числа по процентам |
|---|---|
| Пример 1 | Сумма кредита: 100 000 рублей Срок кредита: 36 месяцев Процентная ставка: 10% |
| Пример 2 | Сумма вклада: 50 000 рублей Процентная ставка: 5% Срок вклада: 5 лет |
| Пример 3 | Стоимость товара: 1 000 рублей Процент скидки: 20% Сумма скидки: 200 рублей |
| Пример 4 | Сумма инвестиции: 10 000 рублей Процент доходности: 8% Срок инвестиции: 10 лет |
Это всего лишь несколько примеров использования расчета чисел по процентам. Эта математическая операция может быть полезной практически в любой ситуации, где требуется вычислить часть от целого или определить конечную сумму при изменении исходной.