Проценты являются одним из фундаментальных понятий в математике и повседневной жизни. Они широко используются в различных сферах, включая финансы, экономику и торговлю. Часто возникают ситуации, когда необходимо найти число по заданному проценту в дроби. Например, вам могут задать вопрос: "50% от какого числа равно 25?". С помощью простого алгоритма можно легко найти ответ на такой вопрос.
Для того чтобы найти число по заданному проценту в дроби, необходимо выполнить всего 4 шага. Первым шагом является запись данного уравнения в виде пропорции, где неизвестное число обозначено буквой "х". Например, для уравнения "50% от х равно 25" запись будет выглядеть следующим образом: "50/100 = x/25". После этого необходимо переписать уравнение в виде произведения крест-накрест.
Вторым шагом является упрощение полученного уравнения. Путем умножения числителя и знаменателя на одно и то же число, можно упростить выражение. В данном случае, числитель уравнения можно умножить на 25, а знаменатель на 50. Это приведет к следующему уравнению: "50 * x = 25 * 100".
Третьим шагом является вычисление полученного уравнения. В данном случае, необходимо решить простое арифметическое выражение: "50 * x = 2500". Путем деления обеих сторон уравнения на 50 получаем ответ: "x = 50". Значит, 50% от числа равно 25.
Четвертым и последним шагом является проверка полученного результата. Для этого подставляем найденное число обратно в исходное уравнение: "50% от 50 = 25". Если равенство выполняется, то ответ верный.
Что такое процент в дроби
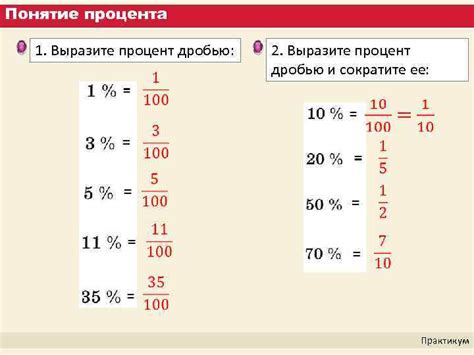
Проценты в дробях позволяют удобно выражать доли или доли от 100 в десятичных форматах, делая их более наглядными и легкими для сравнения. Например, если число 0,75 представить в виде процента, то получим 75%.
Преобразование чисел в процентные дроби – это важный навык, который помогает в работе с процентами, налогами, скидками, процентным соотношением и другими областями, где проценты играют роль.
Шаг 1: Расположение числа по проценту

Для нахождения числа по проценту сначала необходимо определить, где именно в дроби находится это число. Для этого вводим процент в виде десятичной дроби или десятичной формы, например, 0.7 для 70%.
Затем умножаем это число на дробь, в которой числителем является число, которое нам нужно найти, и знаменателем - 100. Это позволяет нам свести проблему к нахождению произведения числа и дроби.
Пример:
Пусть нам нужно найти число, которое составляет 40% от дроби. Мы записываем это как 0.4 и умножаем на дробь вида: [Число / 100]. Таким образом, у нас получается уравнение: 0.4 * (Число / 100).
Шаг 2: Определение числа в процентах

Число в процентах = (Процент ÷ 100) × Число
Где:
- Число в процентах - число, которое мы ищем;
- Процент - значение процента, которое нам известно;
- Число - разделяемая дробь, от которой мы берем процент.
Например, если мы хотим найти число в процентах от дроби 5/8 на основе процента 75%, мы используем формулу:
(75 ÷ 100) × (5/8) = 0.75 × (5/8) = 0.46875
Таким образом, число в процентах от дроби 5/8 на основе 75% равно 0.46875.
Этот шаг помогает нам определить искомое число в процентах от заданной дроби на основе известного процента. Далее мы используем найденное значение для получения окончательного результата.
Пример расчета числа в процентах

Рассмотрим пример расчета числа в процентах.
Допустим, нам дана дробь, состоящая из числителя и знаменателя. Наша задача - найти число, соответствующее проценту этой дроби.
Шаг 1: Найдем десятичное значение дроби. Для этого делим числитель на знаменатель.
Шаг 2: Переведем десятичное значение в проценты. Для этого умножим десятичное значение на 100.
Шаг 3: Округлим полученное значение до необходимого количества знаков после запятой, если требуется.
Шаг 4: Полученное значение является числом, соответствующим проценту данной дроби.
Таким образом, мы можем найти число, соответствующее проценту в дроби, следуя этим четырем простым шагам.
Шаг 3: Нахождение числа по проценту в дроби

Для нахождения числа по проценту в дроби необходимо выполнить следующие шаги:
- Представьте процент в виде десятичной дроби, разделив его на 100. Например, если процент равен 20%, то десятичная дробь будет равна 0,2.
- Умножьте десятичную дробь на число, с которым процент связан. Например, если десятичная дробь равна 0,2, а число равно 150, то результат будет равен 0,2 * 150 = 30.
- Полученный результат будет искомым числом по проценту в дроби. В нашем примере, 30 будет числом, составляющим 20% от числа 150.
При использовании данного метода необходимо учитывать, что процент в дроби может означать различные величины в зависимости от контекста. Например, процент может представлять собой скидку, налог, прибыль и т.д. Поэтому важно правильно интерпретировать процент и использовать его соответствующим образом.
Шаг 4: Проверка правильности решения
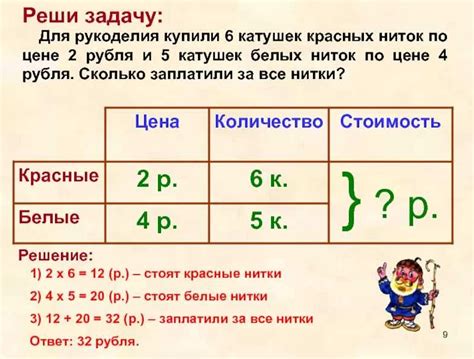
После того как вы рассчитали число по проценту в дроби, необходимо проверить правильность своего решения.
Для этого сравните полученное число со значением, которое было дано в задаче. Если числа совпадают, значит ваше решение верное.
Если числа не совпадают, то возможно допущена ошибка при решении. Перепроверьте каждый из предыдущих шагов, чтобы убедиться, что все действия были выполнены правильно.
Также обратите внимание на единицы измерения, они должны совпадать: если изначальное число было в процентах, то и полученный результат нужно обозначить в процентах.
Проверка правильности решения позволяет убедиться в том, что расчеты выполнены точно и полученный результат соответствует заданному условию.
| Шаг | Описание |
|---|---|
| Шаг 1 | Определение исходного числа и процента в дроби |
| Шаг 2 | Расчет числа, соответствующего проценту |
| Шаг 3 | Вычисление процента в дроби от изначального числа |
| Шаг 4 | Проверка правильности решения |