Физика, как наука, изучает различные явления и законы природы. Одним из важных понятий в физике является давление. Давление – это физическая величина, определяющая отношение силы, действующей на поверхность, к площади этой поверхности. Влияние давления жидкости на окружающие объекты может быть очень значительным и важным для понимания многих процессов.

Давление жидкости возникает в результате взаимодействия молекул жидкости между собой и с поверхностью, на которую эта жидкость действует. Для определения давления жидкости используется специальная формула, которая учитывает как высоту столба жидкости, так и плотность этой жидкости. Формула для расчета давления жидкости имеет вид:

P = ρgh

Где:

• P – давление жидкости
• ρ – плотность жидкости
• g – ускорение свободного падения (9,8 м/с² на поверхности Земли)
• h – высота столба жидкости

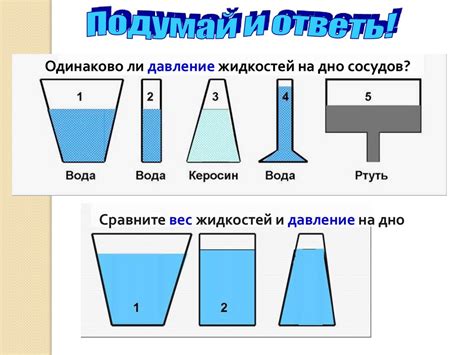
Эта формула позволяет с легкостью определить давление жидкости в заданных условиях. Учитывая значения плотности жидкости и высоты столба, можно получить численное значение давления. Важно отметить, что давление жидкости одинаково в каждой точке на одной и той же глубине внутри жидкости. Это обусловлено тем, что молекулы жидкости находятся в равновесии и действуют с одинаковой силой во всех направлениях.

Понимание давления жидкости в физике является ключевым для объяснения многих явлений, связанных с гидравликой, механикой и другими областями науки. Знание формулы и принципов для расчета давления позволяет более точно предсказывать и объяснять результаты экспериментов и явления, связанные с жидкостями. Разумное использование этой информации может быть полезным не только в академических целях, но и в практических ситуациях, таких как проектирование инженерных систем, создание гидравлических устройств и многое другое.

Формула и принципы расчета давления жидкости

Формулу для расчета давления жидкости можно описать с помощью следующего уравнения:

P = ρgh

Где:

• P - давление жидкости (в паскалях)
• ρ - плотность жидкости (в килограммах на кубический метр)
• g - ускорение свободного падения (в метрах в секунду в квадрате)
• h - высота жидкости (в метрах)

Это уравнение основано на принципе Паскаля, который утверждает, что давление, создаваемое на жидкость в закрытом сосуде, передается в равной мере во всех направлениях и проявляется на всех сторонах сосуда.

Таким образом, при использовании формулы для расчета давления жидкости, необходимо учитывать плотность жидкости, ускорение свободного падения и высоту жидкости. Знание этих параметров позволяет определить силу, с которой жидкость действует на поверхность и ее окружающую среду.

Изучаем физическую сущность

Давление может быть определено как отношение силы, действующей на поверхность, к площади этой поверхности:

P = F/S

Где P - давление, F - сила, действующая на поверхность, S - площадь поверхности.

Более формально, давление жидкости можно определить как отношение суммарной силы, действующей на объем жидкости, к этому объему:

P = F/V

Где V - объем жидкости.

Таким образом, понимая физическую сущность давления жидкости, мы можем использовать соответствующие формулы для его расчета и измерения. Знание этих принципов поможет в решении различных задач и понимании многих явлений, связанных с давлением жидкости в физике.

Поиск формулы для расчета

Для расчета давления жидкости существует несколько формул, которые основываются на определении давления как силы, действующей на единицу площади. Однако, формулу можно подобрать в зависимости от задачи, которую необходимо решить.

Одной из самых простых формул для расчета давления жидкости является формула для статического давления:

1. Обратите внимание на глубину жидкости (h), измеренную от поверхности жидкости до выбранной точки внутри нее.
2. Запишите значение плотности жидкости (ρ).
3. Умножьте значение площади под дном сосуда (A), на которой действует давление, на плотность жидкости (ρ) и ускорение свободного падения (g).
4. Поделите получившееся значение на глубину жидкости (h).
5. Полученный результат будет являться значением давления жидкости в данной точке (P).

Это пример расчета статического давления жидкости, который можно использовать в простых задачах. Однако, в более сложных задачах может потребоваться применение других формул, учитывающих дополнительные факторы, такие как скорость потока или форма сосуда.

Важно помнить, что формулы для расчета давления жидкости являются приближенными и могут не учитывать все факторы, влияющие на давление. Поэтому, при проведении расчетов всегда следует учитывать особенности конкретной задачи и руководствоваться не только формулами, но и общими принципами физики.

Применение принципов в практике

Принципы, описывающие давление жидкости, широко применяются в различных практических областях.

Например, в гидравлике принцип Паскаля о давлении в жидкости используется для создания гидравлических систем, которые используются в различных машинах и механизмах. Такие системы позволяют передавать силу и управлять тяжелыми нагрузками, используя давление жидкости.

В медицине принципы давления жидкости используются для измерения кровяного давления. С помощью специального прибора - тонометра, определяют верхнее и нижнее давление, что позволяет оценить состояние сердечно-сосудистой системы пациента.

Также принципы давления жидкости используются в строительстве. Например, при проектировании и строительстве гидротехнических сооружений, таких как плотины и водохранилища, необходимо учитывать давление воды на конструкцию. Это позволяет обеспечить стабильность сооружения и гарантировать его безопасное использование.

Таким образом, принципы давления жидкости имеют широкое применение и являются неотъемлемой частью ряда практических областей. Их понимание и использование позволяют решать различные задачи и создавать эффективные технические решения.